Detailed explanation of graphic code of C# classic sorting algorithm (Part 1)-C#.Net Tutorial-php.cn

This article mainly introduces the first part of the series of seven classic sorting algorithms in C#, bubble sort, quick sort, etc. It has certain reference value. Interested friends can refer to it

Today is the beginning. I have to talk about algorithms. Algorithms are like swords in program development. Wherever they go, the sword rises and falls.

For real-life sorting problems, the algorithm has seven sharp swords that can help you succeed in horse racing.

First of all, there are four kinds of sorting:

Exchange sorting: including bubble sorting and quick sorting.

Selection sort: including direct selection sort and heap sort.

Insertion sort: including direct insertion sort and Hill sort.

Merge sort: Merge sort.

So today we are talking about exchange sorting. We all know that the sorting provided by the C# class library is quick sorting. In order to make today's fun more interesting,

we design an algorithm to follow the class library Provides quick queue battles. Fight to KO your opponent.

Bubble sorting:

First of all, let’s design the “bubble sort” ourselves. A very realistic example of this kind of sorting is:

I If you grab a handful of sand and put it into the water, the sand will immediately sink to the bottom of the water. The dust on the sand will temporarily sink to the bottom of the water due to inertia, but it will immediately surface like bubbles, and finally the truth will be revealed.

Regarding the bubbling thoughts, I will not talk about such official theories, nor will I post those words. My thoughts are just looking at the pictures.

Then let’s take the picture above.

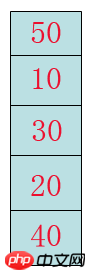
To achieve the bubbling effect, we have to stand up a set of numbers and look at them. Think about it, how bubble? How to understand that the heavy sinks to the bottom and the light floats?

The first step: We compare 40 with 20 and find that 40 is the boss and there is no need to exchange.

The second step: Then take a step forward, that is, compare 20 with 30. If you find that 30 is the boss, you have to exchange.

Step 3: Compare the exchanged 20 with 10, and find that you are the boss and don’t need to exchange.

Step 4: Exchange 10 with 50. If you find that 50 is the boss, make the exchange.

Finally, after a traversal, we sent the smallest number in the array. Look, we have taken another step towards the goal.

Now that everyone knows what they are thinking, we will strongly demand that we compete with quick queue. Either you die or I live.

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Diagnostics;
using System.Threading;

namespace BubbleSort
{
  public class Program
  {
    static void Main(string[] args)
    {
      //五次比较
      for (int i = 1; i <= 5; i++)
      {
        List<int> list = new List<int>();
        //插入2k个随机数到数组中
        for (int j = 0; j < 2000; j++)
        {
          Thread.Sleep(1);
          list.Add(new Random((int)DateTime.Now.Ticks).Next(0, 100000));
        }
        Console.WriteLine("\n第" + i + "次比较：");
        Stopwatch watch = new Stopwatch();
        watch.Start();
        var result = list.OrderBy(single => single).ToList();
        watch.Stop();
        Console.WriteLine("\n快速排序耗费时间：" + watch.ElapsedMilliseconds);
        Console.WriteLine("输出前是十个数:" + string.Join(",", result.Take(10).ToList()));
        watch.Start();
        result = BubbleSort(list);
        watch.Stop();
        Console.WriteLine("\n冒泡排序耗费时间：" + watch.ElapsedMilliseconds);
        Console.WriteLine("输出前是十个数:" + string.Join(",", result.Take(10).ToList()));
      }
    }

    //冒泡排序算法
    static List<int> BubbleSort(List<int> list)
    {
      int temp;
      //第一层循环： 表明要比较的次数，比如list.count个数，肯定要比较count-1次
      for (int i = 0; i < list.Count - 1; i++)
      {
        //list.count-1：取数据最后一个数下标，
//j>i: 从后往前的的下标一定大于从前往后的下标，否则就超越了。
        for (int j = list.Count - 1; j > i; j--)
        {
          //如果前面一个数大于后面一个数则交换
          if (list[j - 1] > list[j])
          {
            temp = list[j - 1];
            list[j - 1] = list[j];
            list[j] = temp;
          }
        }
      }
      return list;
    }
  }
}

Copy after login

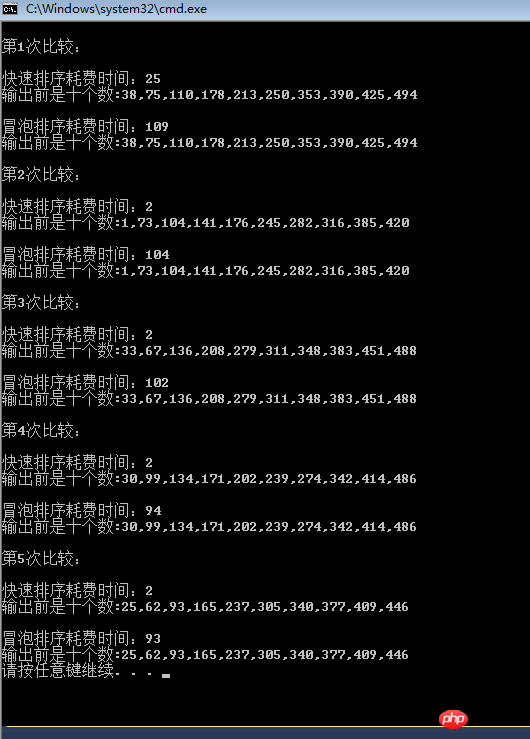
Woo woo, looking at these two sorted physical examination reports, my heart went cold, Bubble was KOed by the quick queue, It's so miserable. No wonder people say that bubbling efficiency is low, but it turns out it is really low.

Quick Sort:

Since we can KO bubbling, our interest was immediately aroused. Why is tnd Quick Sort so fast? We must study it carefully.

First of all, the above picture:

From the picture we can see:

left pointer, right pointer, base reference number.

In fact, the idea is quite simple, which is to find the cutting point of the array through the first pass of traversal (making the left and right pointers coincide).

Step one: First, we take out the number (20) from the left position of the array as the base reference object.

Second step: Search forward from the right position of the array until you find a number smaller than (base).

If found, assign this number to the left position (that is, 10 To 20),

The array at this time is: 10, 40, 50, 10, 60,

LEFT and Right pointers are 10 before and after.

Step 3: Search backward from the left position of the array until you find a number larger than (base).

If found, assign this number to the right position (that is, 40 To 10),

At this time the array is: 10, 40, 50, 40, 60,

Left and Right pointers are 40 before and after.

Step 4: Repeat the "second and third" steps until the left and right pointers coincide,

Finally, insert (base) to the position of 40,

At this time, the array values are: 10, 20, 50, 40, 60. At this point, a sorting is completed.

Step 5: At this time, 20 has sneaked into the interior of the array. The group of numbers on the left side of 20 are smaller than 20, and the group of numbers on the right side of 20 are larger than 20.

以20为切入点对左右两边数按照"第一，第二，第三，第四"步骤进行，最终快排大功告成。

同样，我们把自己设计的快排跟类库提供的快拍比较一下。

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading;
using System.Diagnostics;

namespace QuickSort
{
  public class Program
  {
    static void Main(string[] args)
    {
      //5次比较
      for (int i = 1; i <= 5; i++)
      {
        List<int> list = new List<int>();

        //插入200个随机数到数组中
        for (int j = 0; j < 200; j++)
        {
          Thread.Sleep(1);
          list.Add(new Random((int)DateTime.Now.Ticks).Next(0, 10000));
        }

        Console.WriteLine("\n第" + i + "次比较：");

        Stopwatch watch = new Stopwatch();

        watch.Start();
        var result = list.OrderBy(single => single).ToList();
        watch.Stop();

        Console.WriteLine("\n系统定义的快速排序耗费时间：" + watch.ElapsedMilliseconds);
        Console.WriteLine("输出前是十个数:" + string.Join(",", result.Take(10).ToList()));

        watch.Start();
        new QuickSortClass().QuickSort(list, 0, list.Count - 1);
        watch.Stop();

        Console.WriteLine("\n俺自己写的快速排序耗费时间：" + watch.ElapsedMilliseconds);
        Console.WriteLine("输出前是十个数:" + string.Join(",", list.Take(10).ToList()));

      }
    }
  }

  public class QuickSortClass
  {

    ///<summary>
/// 分割函数
///</summary>
///<param name="list">待排序的数组</param>
///<param name="left">数组的左下标</param>
///<param name="right"></param>
///<returns></returns>
    public int pision(List<int> list, int left, int right)
    {
      //首先挑选一个基准元素
      int baseNum = list[left];

      while (left < right)
      {
        //从数组的右端开始向前找，一直找到比base小的数字为止(包括base同等数)
        while (left < right && list[right] >= baseNum)
          right = right - 1;

        //最终找到了比baseNum小的元素，要做的事情就是此元素放到base的位置
        list[left] = list[right];

        //从数组的左端开始向后找，一直找到比base大的数字为止（包括base同等数）
        while (left < right && list[left] <= baseNum)
          left = left + 1;


        //最终找到了比baseNum大的元素，要做的事情就是将此元素放到最后的位置
        list[right] = list[left];
      }
      //最后就是把baseNum放到该left的位置
      list[left] = baseNum;

      //最终，我们发现left位置的左侧数值部分比left小，left位置右侧数值比left大
//至此，我们完成了第一篇排序
      return left;
    }

    public void QuickSort(List<int> list, int left, int right)
    {
      //左下标一定小于右下标，否则就超越了
      if (left < right)
      {
        //对数组进行分割，取出下次分割的基准标号
        int i = pision(list, left, right);

        //对“基准标号“左侧的一组数值进行递归的切割，以至于将这些数值完整的排序
        QuickSort(list, left, i - 1);

        //对“基准标号“右侧的一组数值进行递归的切割，以至于将这些数值完整的排序
        QuickSort(list, i + 1, right);
      }
    }
  }
}

Copy after login

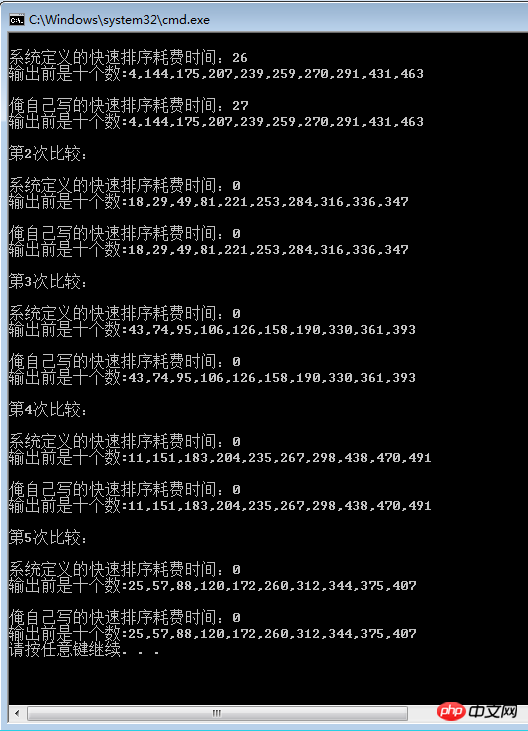
不错，快排就是快，难怪内库非要用他来作为排序的标准。

嗯，最后要分享下：

冒泡的时间复杂度为：0(n) - 0(n^2)

快排的时间复杂度为：

平均复杂度：N(logN)

最坏复杂度： 0(n^2)

The above is the detailed content of Detailed explanation of graphic code of C# classic sorting algorithm (Part 1). For more information, please follow other related articles on the PHP Chinese website!