Python code example to implement Sudoku solving program

Recently I am taking my children to learn Sudoku. Due to my career, I searched online for solutions to related programs. I share them with you here. I hope it will be helpful for everyone to learn python

I accidentally discovered a program that comes with the Linux system I opened the Sudoku game and played a few games. Unfortunately, I am a novice at Sudoku. I have never played Sudoku before, and I couldn’t even take a few steps before getting into a mess.

So I planned to use the powerful computing power of the computer to violently solve Sudoku, which is still very fun.

The following is a record of some of my thoughts and experiences on writing a Sudoku program.

1. The basic solution to the Sudoku game

Programming in general is a methodology. No matter what the program is, the problem-solving process must be broken down into several simple methods that the computer can implement. As the saying goes, simplicity leads to greatness. For a computer that can only understand 0 and 1, it is even more necessary to subdivide the steps and solve the problem step by step.

First, let’s think about the basic concepts of solving Sudoku.

Sudoku has a total of 81 grids, nine horizontally and nine vertically, and is divided into 9 nine-square grids. The rules are simple - the numbers in each grid need to ensure that there are no identical numbers in the horizontal and vertical rows and the nine-square grid.

So our general idea is to try to fill in the number from the first blank, starting from 1. If 1 does not satisfy the requirement of nine horizontal and vertical squares without repetition, then fill in 2, and then fill in 2. By analogy, until a number that temporarily satisfies the rules is filled in, this cell is interrupted, and the process is repeated by moving to the next space.

If you reach a certain space and find that there are countless options, it means that the previous square was filled in incorrectly, then return to the previous square and continue to try 9 from the interruption of the previous square until you return to this point. Go to the wrong box.

In this way, we can sort out the important steps:

•Find the next space
•Take turns filling in the numbers 1 to 9
•Recursively determine whether the filled-in number conforms to the rules

2. Program

Firstly, the Sudoku test was designed by Finnish mathematician Inkara who spent 3 months The most difficult Sudoku ever created in the world. As follows

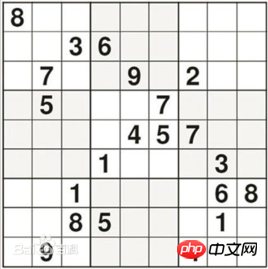
represents the space with 0 and represents the Sudoku as a nested list, so that the number of rows and columns of each grid is exactly the corresponding number of each grid in the list. The index of the number.

The program is as follows:

 #coding=utf-8
 import datetime
 class solution(object):
   def __init__(self,board):
     self.b = board
     self.t = 0
 
   def check(self,x,y,value):#检查每行每列及每宫是否有相同项
     for row_item in self.b[x]:
       if row_item == value:
         return False
     for row_all in self.b:
       if row_all[y] == value:
         return False
     row,col=x/3*3,y/3*3
     row3col3=self.b[row][col:col+3]+self.b[row+1][col:col+3]+self.b[row+2][col:col+3]
     for row3col3_item in row3col3:
       if row3col3_item == value:
         return False
     return True
 
   def get_next(self,x,y):#得到下一个未填项
     for next_soulu in range(y+1,9):
       if self.b[x][next_soulu] == 0:
         return x,next_soulu
     for row_n in range(x+1,9):
       for col_n in range(0,9):
         if self.b[row_n][col_n] == 0:
           return row_n,col_n
     return -1,-1 #若无下一个未填项，返回-1
 
   def try_it(self,x,y):#主循环
     if self.b[x][y] == 0:
       for i in range(1,10):#从1到9尝试
         self.t+=1
         if self.check(x,y,i):#符合 行列宫均无条件 的
           self.b[x][y]=i #将符合条件的填入0格
           next_x,next_y=self.get_next(x,y)#得到下一个0格
           if next_x == -1: #如果无下一个0格
             return True #返回True
           else:    #如果有下一个0格，递归判断下一个0格直到填满数独
             end=self.try_it(next_x,next_y)
             if not end:  #在递归过程中存在不符合条件的，即 使try_it函数返回None的项
               self.b[x][y] = 0  #回朔到上一层继续
             else:
               return True
 
   def start(self):
     begin = datetime.datetime.now()
     if self.b[0][0] == 0:
       self.try_it(0,0)
     else:
       x,y=self.get_next(0,0)
       self.try_it(x,y)
     for i in self.b:
       print i
     end = datetime.datetime.now()
     print '\ncost time:', end - begin
     print 'times:',self.t
     return
 
 
 s=solution([[8,0,0,0,0,0,0,0,0],
     [0,0,3,6,0,0,0,0,0],
     [0,7,0,0,9,0,2,0,0],
     [0,5,0,0,0,7,0,0,0],
     [0,0,0,8,4,5,7,0,0],
     [0,0,0,1,0,0,0,3,0],
     [0,0,1,0,0,0,0,6,8],
     [0,0,8,5,0,0,0,1,0],
     [0,9,0,0,0,0,4,0,0]])
 73 s.start()

It is worth noting that the recursive judgment used can cleverly go back to the previous level when taking the wrong branch. The specific implementation is to use a for loop to continuously fill in numbers from 1 to 9 while reaching the recording break point. Determine whether to backtrack by the return value of the next layer.

The program output is as follows:

[8, 1, 2, 7, 5, 3, 6, 4, 9]
[9, 4, 3, 6, 8, 2, 1, 7, 5]
[6, 7, 5, 4, 9, 1, 2, 8, 3]
[1, 5, 4, 2, 3, 7, 8, 9, 6]
[3, 6, 9, 8, 4, 5, 7, 2, 1]
[2, 8, 7, 1, 6, 9, 5, 3, 4]
[5, 2, 1, 9, 7, 4, 3, 6, 8]
[4, 3, 8, 5, 2, 6, 9, 1, 7]
[7, 9, 6, 3, 1, 8, 4, 5, 2]

cost time: 0:00:00.060687
times: 45360

It can be seen that although the program has many operations, it is still very fast.

The above is the detailed content of Python code example to implement Sudoku solving program. For more information, please follow other related articles on the PHP Chinese website!