 Web Front-end
Web Front-end
 JS Tutorial
JS Tutorial
 Share an example where the number of digits in js is too large, causing parameter precision to be lost.
Share an example where the number of digits in js is too large, causing parameter precision to be lost.
Share an example where the number of digits in js is too large, causing parameter precision to be lost.
Share an example where the number of digits in js is too large, resulting in the loss of parameter precision

I recently encountered a strange problem. When passing a parameter in a js function, a digit is passed. The number is relatively large. If you print arguments, you can see that the passed parameters have changed.

Then I checked and found that it was indeed caused by the loss of js accuracy. My solution is to change the numeric type to character type transmission, so that the accuracy will not be lost. As shown below:
The reason why JS numbers lose precision
The binary implementation of the computer and the number of digits limit some numbers cannot be represented finitely. Just like some irrational numbers cannot be represented finitely, such as pi 3.1415926..., 1.3333... etc. JS complies with IEEE 754 specification, uses double precision storage (double precision), occupying 64 bits. As shown in the figure
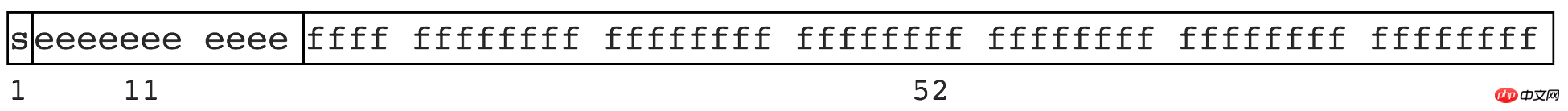
Meaning
1 bit is used to represent the sign bit
11 Bits are used to represent the exponent
52 bits represent the mantissa
Floating point numbers, such as
0.1 >> 0.0001 1001 1001 1001…(1001无限循环) 0.2 >> 0.0011 0011 0011 0011…(0011无限循环)
can only imitate decimal at this time Rounding is done, but there are only two binary numbers, 0 and 1, so it becomes 0 and rounded to 1. This is the root cause of errors and loss of precision in some floating-point number operations in computers.
The precision loss of large integers is essentially the same as that of floating point numbers. The maximum number of mantissa digits is 52. Therefore, the largest integer that can be accurately represented in JS is Math.pow(2, 53), which in decimal is 9007199254740992.
Greater than 9007199254740992 may lose accuracy
9007199254740992 >> 10000000000000...000 // 共计 53 个 0 9007199254740992 + 1 >> 10000000000000...001 // 中间 52 个 0 9007199254740992 + 2 >> 10000000000000...010 // 中间 51 个 0
Actually
9007199254740992 + 1 // 丢失 9007199254740992 + 2 // 未丢失 9007199254740992 + 3 // 丢失 9007199254740992 + 4 // 未丢失
The result is as shown in the figure
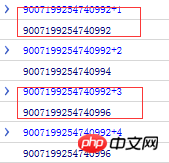
Above, you can We know that seemingly finite numbers are actually infinite in the binary representation of computers. Due to the limitation of storage digits, there is "rounding", and the loss of precision occurs.
想了解更深入的分析可以看这篇论文(又长又臭):What Every Computer Scientist Should Know About Floating-Point Arithmetic
三、解决方案
对于整数,前端出现问题的几率可能比较低,毕竟很少有业务需要需要用到超大整数,只要运算结果不超过 Math.pow(2, 53) 就不会丢失精度。
对于小数,前端出现问题的几率还是很多的,尤其在一些电商网站涉及到金额等数据。解决方式:把小数放到位整数(乘倍数),再缩小回原来倍数(除倍数
// 0.1 + 0.2 (0.1*10 + 0.2*10) / 10 == 0.3 // true
The above is the detailed content of Share an example where the number of digits in js is too large, causing parameter precision to be lost.. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 How to use JS and Baidu Maps to implement map pan function
Nov 21, 2023 am 10:00 AM
How to use JS and Baidu Maps to implement map pan function
Nov 21, 2023 am 10:00 AM
How to use JS and Baidu Map to implement map pan function Baidu Map is a widely used map service platform, which is often used in web development to display geographical information, positioning and other functions. This article will introduce how to use JS and Baidu Map API to implement the map pan function, and provide specific code examples. 1. Preparation Before using Baidu Map API, you first need to apply for a developer account on Baidu Map Open Platform (http://lbsyun.baidu.com/) and create an application. Creation completed
 Recommended: Excellent JS open source face detection and recognition project
Apr 03, 2024 am 11:55 AM
Recommended: Excellent JS open source face detection and recognition project
Apr 03, 2024 am 11:55 AM
Face detection and recognition technology is already a relatively mature and widely used technology. Currently, the most widely used Internet application language is JS. Implementing face detection and recognition on the Web front-end has advantages and disadvantages compared to back-end face recognition. Advantages include reducing network interaction and real-time recognition, which greatly shortens user waiting time and improves user experience; disadvantages include: being limited by model size, the accuracy is also limited. How to use js to implement face detection on the web? In order to implement face recognition on the Web, you need to be familiar with related programming languages and technologies, such as JavaScript, HTML, CSS, WebRTC, etc. At the same time, you also need to master relevant computer vision and artificial intelligence technologies. It is worth noting that due to the design of the Web side
 How to create a stock candlestick chart using PHP and JS
Dec 17, 2023 am 08:08 AM
How to create a stock candlestick chart using PHP and JS
Dec 17, 2023 am 08:08 AM
How to use PHP and JS to create a stock candle chart. A stock candle chart is a common technical analysis graphic in the stock market. It helps investors understand stocks more intuitively by drawing data such as the opening price, closing price, highest price and lowest price of the stock. price fluctuations. This article will teach you how to create stock candle charts using PHP and JS, with specific code examples. 1. Preparation Before starting, we need to prepare the following environment: 1. A server running PHP 2. A browser that supports HTML5 and Canvas 3
 Essential tools for stock analysis: Learn the steps to draw candle charts with PHP and JS
Dec 17, 2023 pm 06:55 PM
Essential tools for stock analysis: Learn the steps to draw candle charts with PHP and JS
Dec 17, 2023 pm 06:55 PM
Essential tools for stock analysis: Learn the steps to draw candle charts in PHP and JS. Specific code examples are required. With the rapid development of the Internet and technology, stock trading has become one of the important ways for many investors. Stock analysis is an important part of investor decision-making, and candle charts are widely used in technical analysis. Learning how to draw candle charts using PHP and JS will provide investors with more intuitive information to help them make better decisions. A candlestick chart is a technical chart that displays stock prices in the form of candlesticks. It shows the stock price
 How to use JS and Baidu Map to implement map click event processing function
Nov 21, 2023 am 11:11 AM
How to use JS and Baidu Map to implement map click event processing function
Nov 21, 2023 am 11:11 AM
Overview of how to use JS and Baidu Maps to implement map click event processing: In web development, it is often necessary to use map functions to display geographical location and geographical information. Click event processing on the map is a commonly used and important part of the map function. This article will introduce how to use JS and Baidu Map API to implement the click event processing function of the map, and give specific code examples. Steps: Import the API file of Baidu Map. First, import the file of Baidu Map API in the HTML file. This can be achieved through the following code:
 How to use JS and Baidu Maps to implement map heat map function
Nov 21, 2023 am 09:33 AM
How to use JS and Baidu Maps to implement map heat map function
Nov 21, 2023 am 09:33 AM
How to use JS and Baidu Maps to implement the map heat map function Introduction: With the rapid development of the Internet and mobile devices, maps have become a common application scenario. As a visual display method, heat maps can help us understand the distribution of data more intuitively. This article will introduce how to use JS and Baidu Map API to implement the map heat map function, and provide specific code examples. Preparation work: Before starting, you need to prepare the following items: a Baidu developer account, create an application, and obtain the corresponding AP
 PHP and JS Development Tips: Master the Method of Drawing Stock Candle Charts
Dec 18, 2023 pm 03:39 PM
PHP and JS Development Tips: Master the Method of Drawing Stock Candle Charts
Dec 18, 2023 pm 03:39 PM
With the rapid development of Internet finance, stock investment has become the choice of more and more people. In stock trading, candle charts are a commonly used technical analysis method. It can show the changing trend of stock prices and help investors make more accurate decisions. This article will introduce the development skills of PHP and JS, lead readers to understand how to draw stock candle charts, and provide specific code examples. 1. Understanding Stock Candle Charts Before introducing how to draw stock candle charts, we first need to understand what a candle chart is. Candlestick charts were developed by the Japanese
 Right-click New in Win10 disappears
Jan 07, 2024 pm 03:57 PM
Right-click New in Win10 disappears
Jan 07, 2024 pm 03:57 PM
Many friends find that New in the list is missing when they right-click on the desktop. What is going on? It may be that the anti-virus software automatically cleans up some files. In fact, we only need to enter the settings and adjust the values to restore it. , let’s take a look at the specific tutorial with the editor. The first step to restore Win10 by right-clicking and creating a new one, "win+R" to open Run, enter: regedit, click "OK", open the Registry Editor. The second step is to expand HKEY_CLASSES_ROOT in the opened Registry Editor window. In HKEY_CLASSES_ROOT Find: Directory in the expanded items, and then expand: Directory\Background





