 Java
Java
 javaTutorial
javaTutorial
 Four ways to swap the values of two variables without using the third variable
Four ways to swap the values of two variables without using the third variable
Four ways to swap the values of two variables without using the third variable
int a,b; a=10; b=15;int t; t=a; a=b; b=t;
This algorithm is easy to understand and is especially suitable for helping beginners understand the characteristics of computer programs. It is a classic application of assignment statements. In actual software development, this algorithm is simple and clear, does not cause ambiguity, and facilitates communication between programmers. Under normal circumstances, this algorithm (hereinafter referred to as the standard algorithm) should be used when encountering the problem of exchanging variable values.
The biggest disadvantage of the above algorithm is that it requires the use of a temporary variable. So can exchange be achieved without the help of temporary variables? The answer is yes! Here we can use three algorithms to implement: 1) arithmetic operations; 2) pointer address operations; 3) bit operations; 4) stack implementation.
1) Arithmetic operation
int a,b; a=10;b=12; a=b-a; //a=2;b=12b=b-a; //a=2;b=10a=b+a; //a=10;b=10
The principle is: treat a and b as points on the number axis, and perform them around the distance between the two points calculate.
Compared with the standard algorithm, this algorithm has three more calculation processes, but does not use temporary variables. (Hereinafter referred to as arithmetic algorithm)
2) Pointer address operation
Because the operation of the address actually performs integer operations, for example: subtracting two addresses to obtain an integer, indicating that the storage locations of the two variables in the memory are separated. How many bytes; the address is added to an integer, that is, "a+10" represents the address of the 10 class a data units after a with a as the base address. Therefore, in theory, the exchange of addresses can be completed through operations similar to arithmetic algorithms, thereby achieving the purpose of exchanging variables. That is:
int *a,*b; //假设*a=new int(10);*b=new int(20); //&a=0x00001000h,&b=0x00001200ha=(int*)(b-a); //&a=0x00000200h,&b=0x00001200hb=(int*)(b-a); //&a=0x00000200h,&b=0x00001000ha=(int*)(b+int(a)); //&a=0x00001200h,&b=0x00001000h
Through the above operation, the addresses of a and b have really been exchanged, and a points to the value originally pointed to by b, and does b point to the value originally pointed to by a? The above code can be compiled, but the execution results are incredible! Why?
if(a<b)
{
a=(int*)(b-a);
b=(int*)(b-(int(a)&0x0000ffff));
a=(int*)(b+(int(a)&0x0000ffff));
}else{
b=(int*)(a-b);
a=(int*)(a-(int(b)&0x0000ffff));
b=(int*)(a+(int(b)&0x0000ffff));
}The biggest improvement of the algorithm is to use the AND operation "int(a)&0x0000ffff" in the bit operation, because the upper 16 bits of the address are the segment address, and the last 16 bits are the displacement address. After ANDing it with 0x0000ffff, the segment address is masked and only the displacement address is retained. This matches the original algorithm and gets the correct result.
This algorithm also completes the exchange of values without using a third variable. Compared with arithmetic algorithms, it is difficult to understand, but it has its advantage, that is, when exchanging large data types, its execution speed is faster than arithmetic. The algorithm is fast. Because it exchanges addresses, but the variable value has not been moved in memory. (Hereinafter referred to as the address algorithm)3) Bit operation
int a=10,b=12; //a=1010^b=1100;a=a^b; //a=0110^b=1100;b=a^b; //a=0110^b=1010;a=a^b; //a=1100=12;b=1010;
The realization of this algorithm is determined by the characteristics of the XOR operation. Through the XOR operation, Some bits in the data are flipped, while other bits are unchanged. This means that any number and any given value are XORed twice in a row, and the value remains unchanged.
int exchange(int x,int y)
{
stack S;
push(S,x);
push(S,y);
x=pop(S);
y=pop(S);
}The above algorithms all realize the exchange of two variable values without the help of other variables. In comparison, the arithmetic algorithm and the bit algorithm have the same amount of calculation, and the calculation in the address algorithm is more complicated. , but can easily realize the exchange of large types (such as custom classes or structures), while the first two can only exchange integer data (in theory, overloading the "^" operator can also realize the exchange of any structure) ).
The above is the detailed content of Four ways to swap the values of two variables without using the third variable. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1378
1378
 52
52
 How to use mdf and mds files
Feb 19, 2024 pm 05:36 PM
How to use mdf and mds files
Feb 19, 2024 pm 05:36 PM
How to use mdf files and mds files With the continuous advancement of computer technology, we can store and share data in a variety of ways. In the field of digital media, we often encounter some special file formats. In this article, we will discuss a common file format - mdf and mds files, and introduce how to use them. First, we need to understand the meaning of mdf files and mds files. mdf is the extension of the CD/DVD image file, and the mds file is the metadata file of the mdf file.
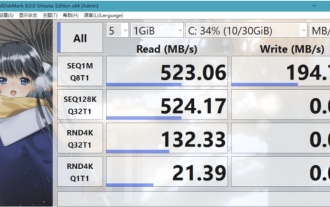 What software is crystaldiskmark? -How to use crystaldiskmark?
Mar 18, 2024 pm 02:58 PM
What software is crystaldiskmark? -How to use crystaldiskmark?
Mar 18, 2024 pm 02:58 PM
CrystalDiskMark is a small HDD benchmark tool for hard drives that quickly measures sequential and random read/write speeds. Next, let the editor introduce CrystalDiskMark to you and how to use crystaldiskmark~ 1. Introduction to CrystalDiskMark CrystalDiskMark is a widely used disk performance testing tool used to evaluate the read and write speed and performance of mechanical hard drives and solid-state drives (SSD). Random I/O performance. It is a free Windows application and provides a user-friendly interface and various test modes to evaluate different aspects of hard drive performance and is widely used in hardware reviews
 How to download foobar2000? -How to use foobar2000
Mar 18, 2024 am 10:58 AM
How to download foobar2000? -How to use foobar2000
Mar 18, 2024 am 10:58 AM
foobar2000 is a software that can listen to music resources at any time. It brings you all kinds of music with lossless sound quality. The enhanced version of the music player allows you to get a more comprehensive and comfortable music experience. Its design concept is to play the advanced audio on the computer The device is transplanted to mobile phones to provide a more convenient and efficient music playback experience. The interface design is simple, clear and easy to use. It adopts a minimalist design style without too many decorations and cumbersome operations to get started quickly. It also supports a variety of skins and Theme, personalize settings according to your own preferences, and create an exclusive music player that supports the playback of multiple audio formats. It also supports the audio gain function to adjust the volume according to your own hearing conditions to avoid hearing damage caused by excessive volume. Next, let me help you
 How to use NetEase Mailbox Master
Mar 27, 2024 pm 05:32 PM
How to use NetEase Mailbox Master
Mar 27, 2024 pm 05:32 PM
NetEase Mailbox, as an email address widely used by Chinese netizens, has always won the trust of users with its stable and efficient services. NetEase Mailbox Master is an email software specially created for mobile phone users. It greatly simplifies the process of sending and receiving emails and makes our email processing more convenient. So how to use NetEase Mailbox Master, and what specific functions it has. Below, the editor of this site will give you a detailed introduction, hoping to help you! First, you can search and download the NetEase Mailbox Master app in the mobile app store. Search for "NetEase Mailbox Master" in App Store or Baidu Mobile Assistant, and then follow the prompts to install it. After the download and installation is completed, we open the NetEase email account and log in. The login interface is as shown below
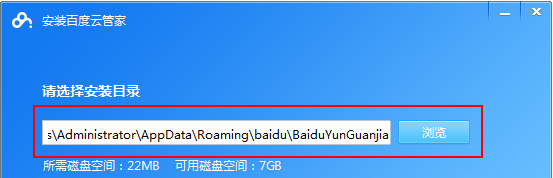 How to use Baidu Netdisk app
Mar 27, 2024 pm 06:46 PM
How to use Baidu Netdisk app
Mar 27, 2024 pm 06:46 PM
Cloud storage has become an indispensable part of our daily life and work nowadays. As one of the leading cloud storage services in China, Baidu Netdisk has won the favor of a large number of users with its powerful storage functions, efficient transmission speed and convenient operation experience. And whether you want to back up important files, share information, watch videos online, or listen to music, Baidu Cloud Disk can meet your needs. However, many users may not understand the specific use method of Baidu Netdisk app, so this tutorial will introduce in detail how to use Baidu Netdisk app. Users who are still confused can follow this article to learn more. ! How to use Baidu Cloud Network Disk: 1. Installation First, when downloading and installing Baidu Cloud software, please select the custom installation option.
 BTCC tutorial: How to bind and use MetaMask wallet on BTCC exchange?
Apr 26, 2024 am 09:40 AM
BTCC tutorial: How to bind and use MetaMask wallet on BTCC exchange?
Apr 26, 2024 am 09:40 AM
MetaMask (also called Little Fox Wallet in Chinese) is a free and well-received encryption wallet software. Currently, BTCC supports binding to the MetaMask wallet. After binding, you can use the MetaMask wallet to quickly log in, store value, buy coins, etc., and you can also get 20 USDT trial bonus for the first time binding. In the BTCCMetaMask wallet tutorial, we will introduce in detail how to register and use MetaMask, and how to bind and use the Little Fox wallet in BTCC. What is MetaMask wallet? With over 30 million users, MetaMask Little Fox Wallet is one of the most popular cryptocurrency wallets today. It is free to use and can be installed on the network as an extension
 How to use Xiaoai Speaker How to connect Xiaoai Speaker to mobile phone
Feb 22, 2024 pm 05:19 PM
How to use Xiaoai Speaker How to connect Xiaoai Speaker to mobile phone
Feb 22, 2024 pm 05:19 PM
After long pressing the play button of the speaker, connect to wifi in the software and you can use it. Tutorial Applicable Model: Xiaomi 12 System: EMUI11.0 Version: Xiaoai Classmate 2.4.21 Analysis 1 First find the play button of the speaker, and press and hold to enter the network distribution mode. 2 Log in to your Xiaomi account in the Xiaoai Speaker software on your phone and click to add a new Xiaoai Speaker. 3. After entering the name and password of the wifi, you can call Xiao Ai to use it. Supplement: What functions does Xiaoai Speaker have? 1 Xiaoai Speaker has system functions, social functions, entertainment functions, knowledge functions, life functions, smart home, and training plans. Summary/Notes: The Xiao Ai App must be installed on your mobile phone in advance for easy connection and use.
 Teach you how to use the new advanced features of iOS 17.4 'Stolen Device Protection'
Mar 10, 2024 pm 04:34 PM
Teach you how to use the new advanced features of iOS 17.4 'Stolen Device Protection'
Mar 10, 2024 pm 04:34 PM
Apple rolled out the iOS 17.4 update on Tuesday, bringing a slew of new features and fixes to iPhones. The update includes new emojis, and EU users will also be able to download them from other app stores. In addition, the update also strengthens the control of iPhone security and introduces more "Stolen Device Protection" setting options to provide users with more choices and protection. "iOS17.3 introduces the "Stolen Device Protection" function for the first time, adding extra security to users' sensitive information. When the user is away from home and other familiar places, this function requires the user to enter biometric information for the first time, and after one hour You must enter information again to access and change certain data, such as changing your Apple ID password or turning off stolen device protection.



