Share commonly used sorting examples in Python
Stability and significance of sorting algorithm
Bubble sort
Complexity and stability Sex
Selection sort
Insertion sort
-
Hill sort
Quick sort
Comparison of efficiency of common sorting algorithms
Stability and significance of sorting algorithms
In the sequence to be sorted, there are records with the same keywords. After sorting, the relative order of these records remains unchanged, then the sorting algorithm is stable.
Unstable sorting cannot complete sorting of multiple keywords. For example, integer sorting, the higher the number of digits, the higher the priority, sorting from high digits to low digits. Then the sorting of each bit requires a stable algorithm, otherwise the correct result cannot be obtained.
That is, When multiple keywords are to be sorted multiple times, a stable algorithm must be used
Bubble sorting
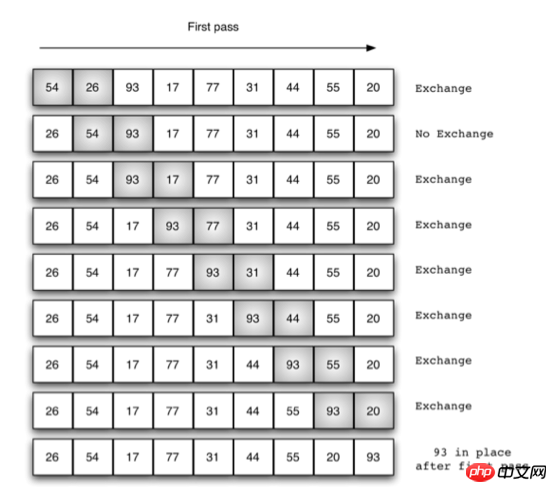 

1 2 3 4 5 6 7 8 9 10 11 12 13 |
|
Complexity and Stability
Optimal time complexity: \(O(n)\) Traversal does not find any elements that can be exchanged, and sorting ends
Worst time complexity: \(O(n^2)\)
- ##Stability: stable

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
|
- Optimal time complexity: O(\(n\)) (ascending order Arrangement, the sequence is already in ascending order)
- Worst time complexity: O(\(n^2\))
- Stability : Stable
increment, and sorts each group using the direct insertion sorting algorithm; as the increment gradually decreases, each group contains more and more keywords. When the amount is reduced to 1, the entire file is divided into one group, and the algorithm terminates.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
|
- Optimum time complexity: \(O(n^{1.3})\) (it does not require itself to be ordered)
- Worst time complexity: \(O(n^2)\) ##Stability: Unstable
Quicksort (Quicksort) divides the data to be sorted into two independent parts through one sorting. All the data in one part is smaller than all the data in the other part. , and then use this method to quickly sort the two parts of the data respectively. The entire sorting process can be performed recursively, so that the entire data becomes an ordered sequence.
The steps are:
- Pick out an element from the sequence, called the "pivot"
- Re- In a sorted sequence, all elements smaller than the base value are placed in front of the base, and all elements larger than the base value are placed behind the base (the same number can go to either side). After this partition, the datum is in the middle of the sequence. This is called a partition operation.
- Recursively sort the subarray of elements smaller than the base value and the subarray of elements greater than the base value.
- The bottom case of recursion is when the size of the array is zero or one, that is, it has always been sorted. Although it continues to recurse, this algorithm will always end, because in each iteration (iteration), it will put at least one element to its final position.
Comparison of efficiency of common sorting algorithms
The above is the detailed content of Share commonly used sorting examples in Python. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1377
1377
 52
52
 Do mysql need to pay
Apr 08, 2025 pm 05:36 PM
Do mysql need to pay
Apr 08, 2025 pm 05:36 PM
MySQL has a free community version and a paid enterprise version. The community version can be used and modified for free, but the support is limited and is suitable for applications with low stability requirements and strong technical capabilities. The Enterprise Edition provides comprehensive commercial support for applications that require a stable, reliable, high-performance database and willing to pay for support. Factors considered when choosing a version include application criticality, budgeting, and technical skills. There is no perfect option, only the most suitable option, and you need to choose carefully according to the specific situation.
 How to use mysql after installation
Apr 08, 2025 am 11:48 AM
How to use mysql after installation
Apr 08, 2025 am 11:48 AM
The article introduces the operation of MySQL database. First, you need to install a MySQL client, such as MySQLWorkbench or command line client. 1. Use the mysql-uroot-p command to connect to the server and log in with the root account password; 2. Use CREATEDATABASE to create a database, and USE select a database; 3. Use CREATETABLE to create a table, define fields and data types; 4. Use INSERTINTO to insert data, query data, update data by UPDATE, and delete data by DELETE. Only by mastering these steps, learning to deal with common problems and optimizing database performance can you use MySQL efficiently.
 Navicat's method to view MongoDB database password
Apr 08, 2025 pm 09:39 PM
Navicat's method to view MongoDB database password
Apr 08, 2025 pm 09:39 PM
It is impossible to view MongoDB password directly through Navicat because it is stored as hash values. How to retrieve lost passwords: 1. Reset passwords; 2. Check configuration files (may contain hash values); 3. Check codes (may hardcode passwords).
 Does mysql need the internet
Apr 08, 2025 pm 02:18 PM
Does mysql need the internet
Apr 08, 2025 pm 02:18 PM
MySQL can run without network connections for basic data storage and management. However, network connection is required for interaction with other systems, remote access, or using advanced features such as replication and clustering. Additionally, security measures (such as firewalls), performance optimization (choose the right network connection), and data backup are critical to connecting to the Internet.
 How to optimize MySQL performance for high-load applications?
Apr 08, 2025 pm 06:03 PM
How to optimize MySQL performance for high-load applications?
Apr 08, 2025 pm 06:03 PM
MySQL database performance optimization guide In resource-intensive applications, MySQL database plays a crucial role and is responsible for managing massive transactions. However, as the scale of application expands, database performance bottlenecks often become a constraint. This article will explore a series of effective MySQL performance optimization strategies to ensure that your application remains efficient and responsive under high loads. We will combine actual cases to explain in-depth key technologies such as indexing, query optimization, database design and caching. 1. Database architecture design and optimized database architecture is the cornerstone of MySQL performance optimization. Here are some core principles: Selecting the right data type and selecting the smallest data type that meets the needs can not only save storage space, but also improve data processing speed.
 HadiDB: A lightweight, horizontally scalable database in Python
Apr 08, 2025 pm 06:12 PM
HadiDB: A lightweight, horizontally scalable database in Python
Apr 08, 2025 pm 06:12 PM
HadiDB: A lightweight, high-level scalable Python database HadiDB (hadidb) is a lightweight database written in Python, with a high level of scalability. Install HadiDB using pip installation: pipinstallhadidb User Management Create user: createuser() method to create a new user. The authentication() method authenticates the user's identity. fromhadidb.operationimportuseruser_obj=user("admin","admin")user_obj.
 Can mysql workbench connect to mariadb
Apr 08, 2025 pm 02:33 PM
Can mysql workbench connect to mariadb
Apr 08, 2025 pm 02:33 PM
MySQL Workbench can connect to MariaDB, provided that the configuration is correct. First select "MariaDB" as the connector type. In the connection configuration, set HOST, PORT, USER, PASSWORD, and DATABASE correctly. When testing the connection, check that the MariaDB service is started, whether the username and password are correct, whether the port number is correct, whether the firewall allows connections, and whether the database exists. In advanced usage, use connection pooling technology to optimize performance. Common errors include insufficient permissions, network connection problems, etc. When debugging errors, carefully analyze error information and use debugging tools. Optimizing network configuration can improve performance
 Does mysql need a server
Apr 08, 2025 pm 02:12 PM
Does mysql need a server
Apr 08, 2025 pm 02:12 PM
For production environments, a server is usually required to run MySQL, for reasons including performance, reliability, security, and scalability. Servers usually have more powerful hardware, redundant configurations and stricter security measures. For small, low-load applications, MySQL can be run on local machines, but resource consumption, security risks and maintenance costs need to be carefully considered. For greater reliability and security, MySQL should be deployed on cloud or other servers. Choosing the appropriate server configuration requires evaluation based on application load and data volume.




