Detailed examples of subset sum problems
Note: Because the study of "subsets and problems" is not in-depth enough, this article may have unclear descriptions or errors in explaining the dynamic programming recursion formula. If you find any, I hope you can Don’t hesitate to teach me.
The subset sum problem can be described as follows: Given n positive integers W=(w1, w2, …, wn) and the positive integer M are required to find such A subsetI⊆{1, 2, 3, ..., n},so that∑wi=M,i∈I[1] . Take an example to give a popular explanation of the subset sum problem: Set W=(1, 2, 3, 4, 5), given a positive integer M =5, whether there is a subset I of W such that the subset ## The sum of the elements in #I is equal to M. In this example, there is obviously a subset I=(2, 3).
Problem definition: Positive integer setS=(w1, w2, w3, …, wn), given a positive Integer W, i in s[i, j] represents # A subset of ##S, j represents the sum of the subset i. If the sum of elements S of a certain set i#j=M, That is, the problem has a solution. Example: S=(7, 34, 4, 12, 5, 3)
,W=6, whether there is a subset of S, the sum of its elements is equal to W. There are also many solutions to this problem. In this article, we use the idea of dynamic programming to solve it, so we need to derive a recursive formula. We continuously divide the set S
into small sets. This is the first step ofdynamic programming: defining the sub-problem . The smallest set of set S is the empty set. Of course, the empty set does not exist and the sum of its elements is equal to W. Of course, if## In the case of #j=0, the empty set is eligible.
The columns of this table represent the sum of the elements in the set. It can only reach the element W at most. It is of course meaningless if it is greater than W. . As long as 1 appears in the j=6 column, the solution to the problem is obtained. The row represents a subset composed of the first i (including i) elements (this sentence may be a bit doubtful, isn’t this Can’t scan everything? Read on). i=0 represents the empty set.
When we define j=6, the empty set situation is true. Then when j=0, this is true for any subset sum (the empty set is their subset). So the form continues to populate as shown below.
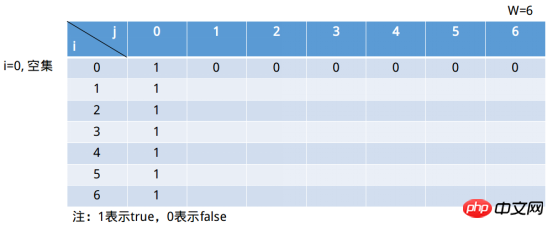
These are actually the third step of dynamic programming: defining the initial state. The second step of state planning is to define state transition rules, that is, the recursive relationship between states.
The i in s[i, j] represents the first i Subset (includes i). In fact, we divide it into two parts from here:
1) Excluding the first i# of the ith element ## subset, that is, s[i - 1, j];
2) Includes thei The first i subset of elements. It is easier to understand the
1) situation. The sum of the first i - 1 set elements is equal to j, then the sum of the subset elements of the first i set elements is equal to j.
What is difficult to understand is the 2) situation. One thing that can be made clear about the second situation is that the i in s[i, X] is certain, and the key is j, jHow to define it at this time? Using "Special value method" in mathematics, take the example set(3, 34, 9), whether there is a sum of elements of a given subset equal to 37, at this time i=2 (subset is (3, 34)), j = 37, at this time “Includes the first i subset of the i element”This kind In the case, s[2, 37] => s[2, 37 - 34] = s[2, 3], subset (3 , 34) Of course there is a subset whose sum of elements is equal to 3. Then if j = 36, s[2, 36] => s[2, 36 - 34] = s[2, 2], the subset (3, 34) obviously does not exist and the sum of its subset elements is equal to 2. What about j = 1, s[2, 1] => s[2, 1 - 34] = s[2, -32],j - wi < 0, at this time s[2, 1] => s[2 - 1, 1] = s[1, 1], subset (3) obviously does not exist and the sum of its subset elements is equal to 1.
In summary, the recursive formula is as follows:

Before implementing this algorithm in code, first fill in the above through the recursive formula matrix.
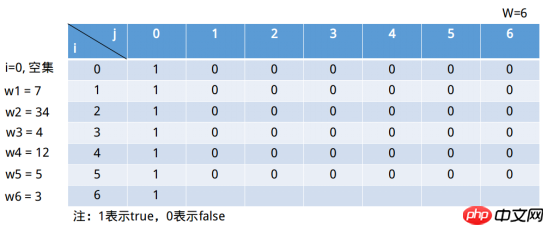
①i = 1, The subset at this time is (7), j = 1, j ∉ (∅), selection situation2) => s[0, 1] || s[1, -6] (i = 0 represents the empty set). Obviously s[1, 1] = 0.
②i = 1, The subset at this time is (7), j = 2, j ∉ (∅), selection situation2) => s[0, 2] || s[1, -5](i = 0 represents the empty set). Obviously s[1, 2] = 0.
……
⑥i = 1, at this time the subset is (7), j = 6, j ∉ (∅), selection situation 2) => s[0, 6] || s[1 , -1] (i = 0 represents the empty set). Obviously s[1, 6] = 0.

The final filling is as shown below:
Continue to fill in the final One line:
①i = 6, The subset at this time is(7, 34, 4, 12, 5, 3),j = 1, j ∉ (7, 34, 4, 12, 5), selection situation 2) => ; s[5, 1] || s[6, -2] (i = 0 represents the empty set). Obviously s[6, 1] = 0.
②i = 6, The subset at this time is (7, 34, 4, 12, 5, 3), j = 2, j ∉ (7, 34, 4, 12, 5), selection situation 2) => s[5, 1] || s[6, -1] (i = 0 represents the empty set). Obviously s[6, 2] = 0.
③i = 6, The subset at this time is (7, 34, 4, 12, 5, 3), j = 3, j ∉ (7, 34, 4, 12, 5), selection situation 2) => s[5, 1] | | s[6, 0]. Obviously s[6, 3] = 1.
...
⑥i = 6, The subset at this time is(7, 34, 4, 12, 5, 3), j = 6, j ∉ (7, 34, 4, 12, 5), selection situation2) => s[5, 6] || s[6, 3]. Obviously s[6, 6] = 1.

Java
## 1 package com.algorithm.dynamicprogramming; 2 3 import java.util.Arrays; 4 5 /** 6 * 子集和问题 7 * Created by yulinfeng on 7/2/17. 8 */ 9 public class SubsetSumProblem {10 11 public static void main(String[] srgs) {12 int[] sets = {7, 34, 4, 12, 5, 3};13 int sum = 87;14 boolean isExistSubSet = subsetSumProblem(sets, sum);15 System.out.println("集合" + Arrays.toString(sets) + "是否存在子集的和等于" + sum + ":" + isExistSubSet);16 }17 18 private static boolean subsetSumProblem(int[] sets, int sum) {19 int row = sets.length + 1;20 int col = sum + 1;21 int[][] solutionMatrix = new int[row][col];22 solutionMatrix[0][0] = 1;23 24 /**25 * 0 1 2 3 4 5 626 * 0 |1|0|0|0|0|0|0|27 * 1 |x|x|x|x|x|x|x|28 * 2 |x|x|x|x|x|x|x|29 * 3 |x|x|x|x|x|x|x|30 * 3 |x|x|x|x|x|x|x|31 * 4 |x|x|x|x|x|x|x|32 * 5 |x|x|x|x|x|x|x|33 * 6 |x|x|x|x|x|x|x|34 */35 for (int i = 1; i < col; i++) {36 solutionMatrix[0][i] = 0;37 }38 /**39 * 初始状态40 * 0 1 2 3 4 5 641 * 0 |1|0|0|0|0|0|0|42 * 1 |1|0|x|x|x|x|x|43 * 2 |x|x|x|x|x|x|x|44 * 3 |x|x|x|x|x|x|x|45 * 3 |x|x|x|x|x|x|x|46 * 4 |x|x|x|x|x|x|x|47 * 5 |x|x|x|x|x|x|x|48 * 6 |1|0|0|x|x|x|x|49 * [i][0] = 1,按行填充50 */51 for (int i = 1; i < row; i++) {52 solutionMatrix[i][0] = 1;53 for (int j = 1; j < col; j++) {54 solutionMatrix[i][j] = solutionMatrix[i - 1][j];55 56 if (solutionMatrix[i][j] == 1) {57 solutionMatrix[i][j] = solutionMatrix[i][j];58 } else if ( j - sets[i - 1] >= 0 && solutionMatrix[i][j - sets[i - 1]] == 1) {59 solutionMatrix[i][j] = solutionMatrix[i][j - sets[i - 1]];60 } else {61 solutionMatrix[i][j] = 0;62 }63 64 if (j == col - 1 && solutionMatrix[i][j] == 1) {65 return true;66 }67 }68 }69 70 return false;71 }72 }Python3
1 def subset_sum_problem(sets, sum): 2 row = len(sets) + 1 3 col = sum + 1 4 solutionMatrix = [[0 for col in range(col)] for row in range(row)] 5 solutionMatrix[0][0] = 1 6 for i in range(1, col): 7 solutionMatrix[0][i] = 0 8 9 for j in range(1, row):10 solutionMatrix[j][0] = 111 for k in range(1, col):12 solutionMatrix[j][k] = solutionMatrix[j - 1][k]13 if solutionMatrix[j][k] == 1:14 solutionMatrix[j][k] = solutionMatrix[j][k]15 elif (k - sets[j - 1] >= 0) and (solutionMatrix[j][k - sets[j - 1]] == 1):16 solutionMatrix[j][k] = solutionMatrix[j][k - sets[j - 1]]17 else:18 solutionMatrix[j][k] = 019 if k == col - 1 and solutionMatrix[j][k] == 1:20 return True21 22 return False23 24 sets = [7, 34, 4, 12, 5, 3]25 num = 626 is_exist = subset_sum_problem(sets, num)27 print(is_exist)
The above is the detailed content of Detailed examples of subset sum problems. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1386
1386
 52
52
 Solve the 'error: redefinition of class 'ClassName'' problem that appears in C++ code
Aug 25, 2023 pm 06:01 PM
Solve the 'error: redefinition of class 'ClassName'' problem that appears in C++ code
Aug 25, 2023 pm 06:01 PM
Solve the "error:redefinitionofclass'ClassName'" problem in C++ code. In C++ programming, we often encounter various compilation errors. One of the common errors is "error:redefinitionofclass 'ClassName'" (redefinition error of class 'ClassName'). This error usually occurs when the same class is defined multiple times. This article will
 Clustering effect evaluation problem in clustering algorithm
Oct 10, 2023 pm 01:12 PM
Clustering effect evaluation problem in clustering algorithm
Oct 10, 2023 pm 01:12 PM
The clustering effect evaluation problem in the clustering algorithm requires specific code examples. Clustering is an unsupervised learning method that groups similar samples into one category by clustering data. In clustering algorithms, how to evaluate the effect of clustering is an important issue. This article will introduce several commonly used clustering effect evaluation indicators and give corresponding code examples. 1. Clustering effect evaluation index Silhouette Coefficient Silhouette coefficient evaluates the clustering effect by calculating the closeness of the sample and the degree of separation from other clusters.
 PHP algorithm analysis: How to use dynamic programming algorithm to solve the longest palindrome substring problem?
Sep 19, 2023 pm 12:19 PM
PHP algorithm analysis: How to use dynamic programming algorithm to solve the longest palindrome substring problem?
Sep 19, 2023 pm 12:19 PM
PHP algorithm analysis: How to use dynamic programming algorithm to solve the longest palindrome substring problem? Dynamic Programming (Dynamic Programming) is a commonly used algorithm idea that can solve many complex problems. One of them is the longest palindrome substring problem, which is to find the length of the longest palindrome substring in a string. This article will introduce how to use PHP to write a dynamic programming algorithm to solve this problem, and provide specific code examples. Let’s first define the longest palindrome substring. A palindrome string refers to a string that reads the same forward and backward, and the palindrome string
 Teach you how to diagnose common iPhone problems
Dec 03, 2023 am 08:15 AM
Teach you how to diagnose common iPhone problems
Dec 03, 2023 am 08:15 AM
Known for its powerful performance and versatile features, the iPhone is not immune to the occasional hiccup or technical difficulty, a common trait among complex electronic devices. Experiencing iPhone problems can be frustrating, but usually no alarm is needed. In this comprehensive guide, we aim to demystify some of the most commonly encountered challenges associated with iPhone usage. Our step-by-step approach is designed to help you resolve these common issues, providing practical solutions and troubleshooting tips to get your equipment back in peak working order. Whether you're facing a glitch or a more complex problem, this article can help you resolve them effectively. General Troubleshooting Tips Before delving into specific troubleshooting steps, here are some helpful
 How to write a dynamic programming algorithm using C#
Sep 20, 2023 pm 04:03 PM
How to write a dynamic programming algorithm using C#
Sep 20, 2023 pm 04:03 PM
How to use C# to write dynamic programming algorithm Summary: Dynamic programming is a common algorithm for solving optimization problems and is suitable for a variety of scenarios. This article will introduce how to use C# to write dynamic programming algorithms and provide specific code examples. 1. What is a dynamic programming algorithm? Dynamic Programming (DP) is an algorithmic idea used to solve problems with overlapping subproblems and optimal substructure properties. Dynamic programming decomposes the problem into several sub-problems to solve, and records the solution to each sub-problem.
 How to solve the problem that jQuery cannot obtain the form element value
Feb 19, 2024 pm 02:01 PM
How to solve the problem that jQuery cannot obtain the form element value
Feb 19, 2024 pm 02:01 PM
To solve the problem that jQuery.val() cannot be used, specific code examples are required. For front-end developers, using jQuery is one of the common operations. Among them, using the .val() method to get or set the value of a form element is a very common operation. However, in some specific cases, the problem of not being able to use the .val() method may arise. This article will introduce some common situations and solutions, and provide specific code examples. Problem Description When using jQuery to develop front-end pages, sometimes you will encounter
 How to use the knapsack problem algorithm in C++
Sep 21, 2023 pm 02:18 PM
How to use the knapsack problem algorithm in C++
Sep 21, 2023 pm 02:18 PM
How to use the knapsack problem algorithm in C++ The knapsack problem is one of the classic problems in computer algorithms. It involves how to select some items to put into the knapsack under a given knapsack capacity to maximize the total value of the items. This article will introduce in detail how to use the dynamic programming algorithm in C++ to solve the knapsack problem, and give specific code examples. First, we need to define the input and output of the knapsack problem. The input includes the weight array wt[] of the item, the value array val[] of the item, and the capacity W of the backpack. The output is which objects are selected
 Label acquisition problem in weakly supervised learning
Oct 08, 2023 am 09:18 AM
Label acquisition problem in weakly supervised learning
Oct 08, 2023 am 09:18 AM
The label acquisition problem in weakly supervised learning requires specific code examples. Introduction: Weakly supervised learning is a machine learning method that uses weak labels for training. Different from traditional supervised learning, weakly supervised learning only needs to use fewer labels to train the model, rather than each sample needs to have an accurate label. However, in weakly supervised learning, how to accurately obtain useful information from weak labels is a key issue. This article will introduce the label acquisition problem in weakly supervised learning and give specific code examples. Introduction to the label acquisition problem in weakly supervised learning:




