Recommended resources for Mahout video tutorials

Mahout provides some scalable implementations of classic algorithms in the field of machine learning, aiming to help developers create intelligent applications more conveniently and quickly. Mahout contains many implementations, including clustering, classification, recommendation filtering, and frequent sub-item mining. Additionally, Mahout can efficiently scale to the cloud by using the Apache Hadoop library.

The teacher’s teaching style:

The teacher’s lectures are simple and easy to understand, clear in structure, analyzed layer by layer, interlocking, and rigorous in argumentation , has a rigorous structure, uses the logical power of thinking to attract students' attention, and uses reason to control the classroom teaching process. By listening to the teacher's lectures, students not only learn knowledge, but also receive thinking training, and are also influenced and influenced by the teacher's rigorous academic attitude

The more difficult point in this video is the logistic regression classifier_Bei Yess Classifier_1:

1. Background

First of all, at the beginning of the article, let’s ask a few questions , if you can answer these questions, then you don’t need to read this article, or your motivation for reading is purely to find faults with this article. Of course, I also welcome it. Please send an email to "Naive Bayesian of Faults" to 297314262 @qq.com, I will read your letter carefully.

By the way, if after reading this article, you still can’t answer the following questions, then please notify me by email and I will try my best to answer your doubts.

The "naive" in the naive Bayes classifier specifically refers to what characteristics of this classifier

Naive Bayes classifier and maximum likelihood estimation (MLE), maximum posterior The relationship between probability (MAP)

The relationship between naive Bayes classification, logistic regression classification, generative model, and decision model

The relationship between supervised learning and Bayesian estimation

2. Agreement

So, this article begins. First of all, regarding the various expression forms that may appear in this article, some conventions are made here

Capital letters, such as X, represent random variables; if X is a multi-dimensional variable, then the subscript i represents the i-th dimension variable, That is, Xi

lowercase letters, such as Xij, represent one value of the variable (the jth value of Xi)

3. Bayesian estimation and supervised learning

Okay, so first answer the fourth question, how to use Bayesian estimation to solve supervised learning problems?

For supervised learning, our goal is actually to estimate an objective function f: X->Y,, or target distribution P(Y|X), where The variable, Y, is the actual classification result of the sample. Assume that the value of sample |X=xk), just find all the estimates of P(X=xk|Y=yi) and all the estimates of P(Y=yi) based on the sample. The subsequent classification process is to find the largest yi of P(Y=yi|X=xk). It can be seen that using Bayesian estimation can solve the problem of supervised learning.

4. The "simple" characteristics of the classifier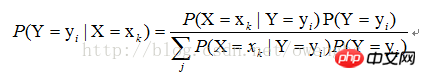

Next, answer the first question, what is "simple"?

From the analysis in Section 3, we know that to obtain P(Y=yi|X=xk), we need to know all the estimates of P(X=xk|Y=yi), as well as P( Y=yi), then assume that There are also two categories, so you need to find 2*(2^N - 1) estimates (note that since Y is given as a certain category, the sum of the probabilities of each value of X is 1, so the actual The value that needs to be estimated is 2^N - 1). As you can imagine, for situations where N is very large (the possible values ​​of term are very large during text classification), the amount of calculation required for this estimation is huge. So how to reduce the amount of estimation required and make the Bayesian estimation method feasible? Here, an assumption is introduced:

Assumption: Under the given condition Y=yi, the dimensional variables of X are independent of each other.

Then, under this assumption, P(X=xk|Y=yi)=P(X1=x1j1|Y=yi)P(X2=x2j2|Y=yi)... P(Xn=xnjn|Y=yi), that is to say, at this time only N estimates are required. Therefore, this assumption reduces the computational complexity of Bayesian estimation from 2*(2^N - 1) to N, making this classifier practical. This assumption then becomes a naive property.

5. Maximum likelihood estimation and maximum posterior probability solution

Next, to answer the second question, our first choice is to apply the maximum likelihood estimation method to naive Bayes classification The solution process of the device.

As mentioned above, the solution of P(X=xk|Y=yi) can be transformed into the solution of P(X1=x1j1|Y=yi), P(X2=x2j2|Y=yi),... P (Xn=xnjn|Y=yi), then how to use the maximum likelihood estimation method to find these values?

First choice We need to understand what maximum likelihood estimation is. In fact, in our probability theory textbooks, the explanations about maximum likelihood estimation are all about solving unsupervised learning problems. After reading After reading this section, you should understand that using maximum likelihood estimation to solve supervised learning problems under naive characteristics is actually using maximum likelihood estimation to solve unsupervised learning problems under various categories of conditions.

The above is the detailed content of Recommended resources for Mahout video tutorials. For more information, please follow other related articles on the PHP Chinese website!