An example explains how Python implements the graph traversal function based on the backtracking method subset tree template

This article mainly introduces the graph traversal function of Python based on the backtracking method subset tree template, and analyzes the related operating skills and precautions of Python using the backtracking method subset tree template for graph traversal problems in the form of examples. Friends who need it can Refer to the following

The example in this article describes how Python implements the graph traversal function based on the backtracking method subset tree template. Share it with everyone for your reference, the details are as follows:

Question

A picture:

A --> B
A --> C
B --> C
B --> D
B --> E
C --> A
C --> D
D --> C
E --> F
F --> C
F --> D

Starts from a node E in the graph and passes through all other nodes without repetition After the node, it returns to the starting node E, which is called a path. Please find all possible paths.

Analysis

Visualize this graph as follows:

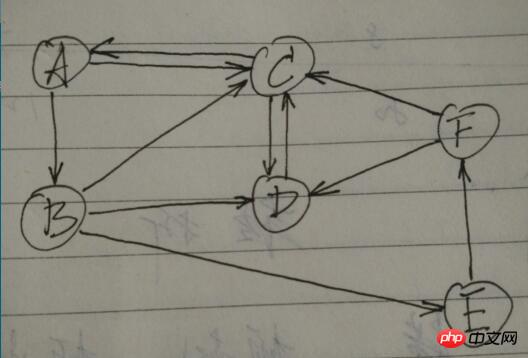
This question involves Graph, then we must first consider what kind of storage structure the graph is represented by. Adjacency matrices, adjacency lists,...are not familiar to me.

The previous article http://www.jb51.net/article/122927.htm has the simplest adjacency list representation.

Next, analyze the problem itself:

Obviously, the length of the solution to the problem is fixed, that is, all path lengths are fixed: n (without returning to the starting node) Or n+1 (return to the starting node)

Each node has its own adjacent nodes.

For a node, all its adjacent nodes can be regarded as the state space of this node. Traverse its state space, prune, and recurse depth-first to the next node. Done!

At this point, it is obvious to apply the backtracking method subset tree template.

Code:

##

'''
图的遍历
从一个节点出发，不重复地经过所有其它节点后，回到出发节点。找出所有的路径
'''
# 用邻接表表示图
n = 6 # 节点数
a,b,c,d,e,f = range(n) # 节点名称
graph = [
  {b,c},
  {c,d,e},
  {a,d},
  {c},
  {f},
  {c,d}
]
x = [0]*(n+1) # 一个解（n+1元数组，长度固定）
X = []     # 一组解
# 冲突检测
def conflict(k):
  global n,graph,x
  # 第k个节点，是否前面已经走过
  if k < n and x[k] in x[:k]:
    return True
  # 回到出发节点
  if k == n and x[k] != x[0]:
    return True
  return False # 无冲突
# 图的遍历
def dfs(k): # 到达（解x的）第k个节点
  global n,a,b,c,d,e,f,graph,x,X
  if k > n: # 解的长度超出，已走遍n+1个节点 （若不回到出发节点，则 k==n）
    print(x)
    #X.append(x[:])
  else:
    for node in graph[x[k-1]]: # 遍历节点x[k]的邻接节点（x[k]的所有状态）
      x[k] = node
      if not conflict(k): # 剪枝
        dfs(k+1)
# 测试
x[0] = e # 出发节点
dfs(1)  # 开始处理解x中的第2个节点

Rendering:

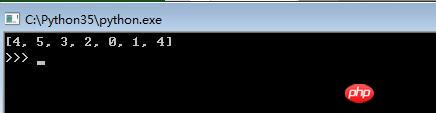
The above is the detailed content of An example explains how Python implements the graph traversal function based on the backtracking method subset tree template. For more information, please follow other related articles on the PHP Chinese website!