js implements data structure: tree and binary tree, binary tree traversal and basic operation methods

Tree structure is a very important type of nonlinear structure. Intuitively, a tree structure is a hierarchical structure defined by branching relationships.

Trees are also widely used in the computer field. For example, in compilers, trees are used to represent the grammatical structure of the source program; in database systems, trees can be used to organize information; when analyzing the behavior of algorithms , trees can be used to describe its execution process, etc.

First, let’s look at some concepts of trees: 1. Tree (Tree) is a finite set of n (n>=0) nodes. In any non-empty tree:

　 (1) There is and is only one specific node called the root;

　 (2) When n>1, The remaining nodes can be divided into m (m>0) mutually disjoint finite sets T1, T2, T3,...Tm, each of which is itself a tree and is called the subtree of the root.

For example, (a) is a tree with only one root node; (b) is a tree with 13 nodes, where A is the root, and the remaining nodes are divided into 3 disjoint subsets: T1={B,E,F,K,L},t2={D,H,I,J,M};T1, T2 and T3 are all subtrees of root A and are themselves a tree.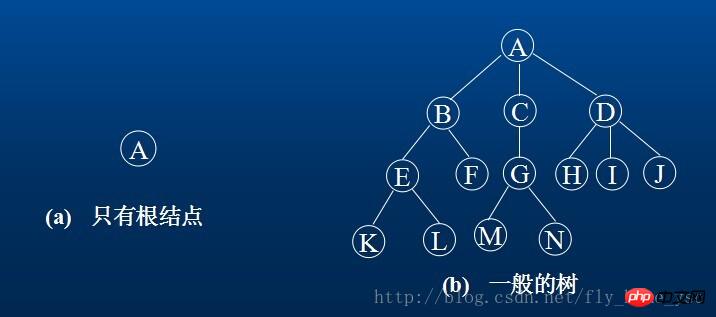

2. The node of the tree contains a data element and several branches pointing to its subtrees. The number of subtrees a node has is called the degree of the node. For example, in (b), the degree of A is 3, the degree of C is 1, and the degree of F is 0. The node with degree 0 is called a leaf or terminal node. Nodes with degree other than 0 are called non-terminal nodes or branch nodes. The degree of a tree is the maximum degree of each node in the tree. The degree of the tree in (b) is 3. The root of the subtree of a node is called the child of the node. Correspondingly, this node is called the child's parent. Children of the same parents call each other siblings. The ancestors of a node are all nodes on the branches from the root to the node. On the contrary, any node in the subtree rooted at a node is called a descendant of that node.

3. The node level (Level) is defined starting from the root, the root is the first level, and the following children are the second level. If a node is at level l, then the root of its subtree is at level l+1. The nodes whose parents are on the same level are cousins ​​of each other. For example, nodes G and E, F, H, I, and J are cousins ​​of each other. The maximum level of nodes in the tree is called the depth or height of the tree. The depth of the tree in (b) is 4.

4. If the subtrees of the nodes in the tree are viewed as ordered from left to right (that is, they cannot be exchanged), then the tree is called an ordered tree, otherwise it is called an unordered tree. In an ordered tree, the root of the leftmost subtree is called the first child, and the root of the rightmost subtree is called the last child.

5. Forest is a collection of m (m>=0) disjoint trees. For each node in the tree, the set of its subtrees is the forest.

Let’s take a look at concepts related to binary trees:

Binary Tree is another tree structure. Its characteristic is that each node has at most two subtrees (i.e. binary tree). There is no node with degree greater than 2), and the subtrees of a binary tree can be divided into left and right subtrees (the order cannot be reversed arbitrarily.)

Properties of binary trees:

1. In the binary tree There are at most 2 i-1 power nodes on the i-th layer (i>=1).

　2. A binary tree with depth k has at most 2 k-th power - 1 nodes, (k>=1).

　3. For any binary tree T, if the number of terminal nodes is n0 and the number of nodes with degree 2 is n2, then n0 = n2 + 1;

　The depth of the tree is k And a binary tree with 2 k-1 nodes is called a full binary tree.

A binary tree with n nodes of depth k, if and only if each node corresponds to the nodes numbered from 1 to n in the full binary tree of depth k, It is called a complete binary tree.

The following are two characteristics of a complete binary tree:

4. The depth of a complete binary tree with n nodes is Math.floor(log 2 n) + 1

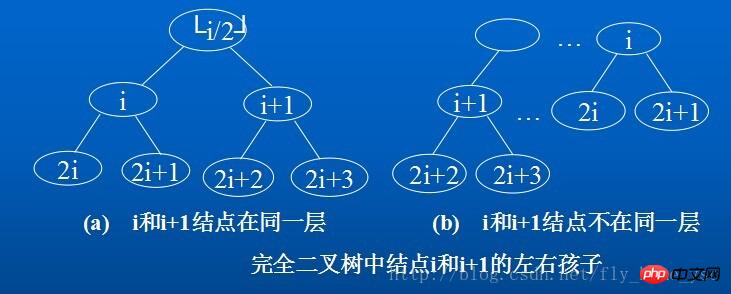
5. If the nodes of a complete binary tree with n nodes (its depth is Math.floor(log 2 n) + 1) are numbered in layer order (from the 1st level to the Math.floor(2 n) + 1, each layer from left to right), then for any node (1

　　(1) If i=1, then node i is a binary tree Root, no parents; if i>1, then its parent(i) is the node Math.floor(i/2).

　　(2) If 2i > n, then node i has no left child (node ​​i is a leaf node); otherwise its left child LChild(i) is node 2i.

　　(3) If 2i + 1 > n, then node i has no right child; otherwise its right child RChild(i) is node 2i + 1;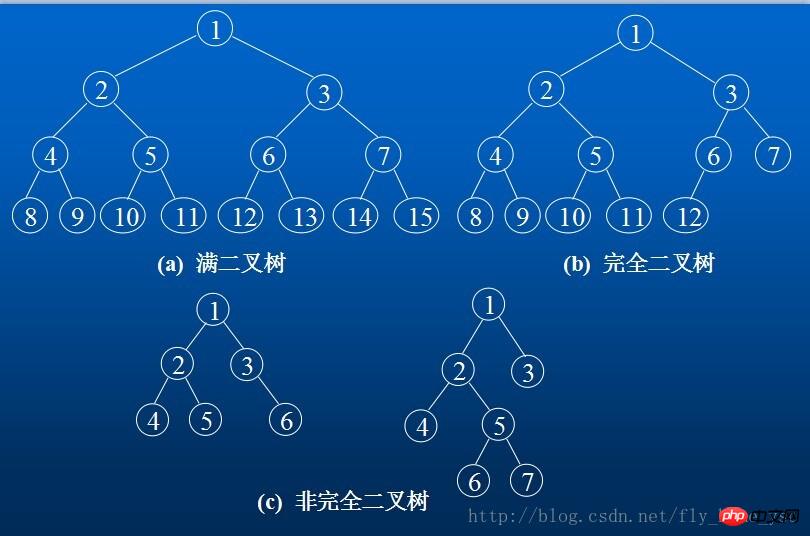

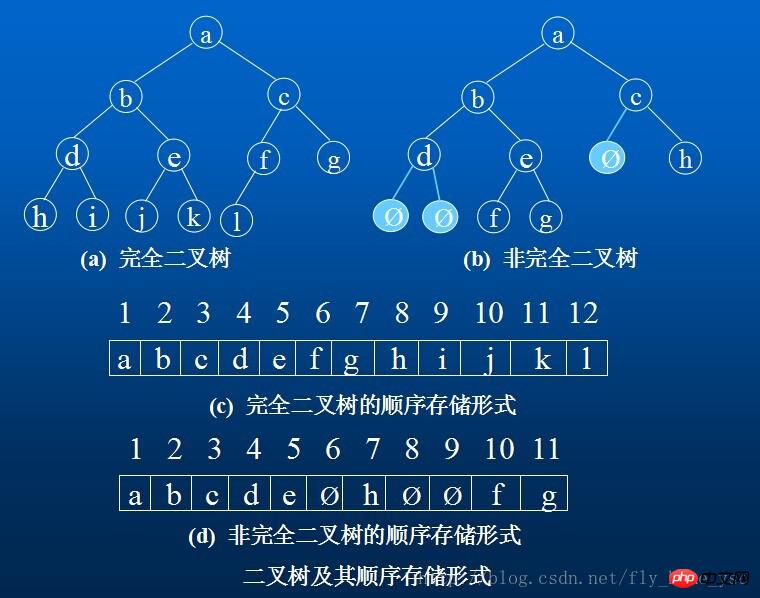
##Storage structure of binary tree

1. Sequential storage structure
Use a set of continuous storage units to store the node elements on the complete binary tree from top to bottom and from left to right, that is, the node element numbered i on the binary tree is stored in the In the component with subscript i-1 in the one-dimensional array defined above. "0" means that this node does not exist. This sequential storage structure is only suitable for complete binary trees.
Because, in the worst case, a single tree with depth k and only k nodes (there is no node with degree 2 in the tree) requires a length of 2 to the nth power -1 dimensional array.

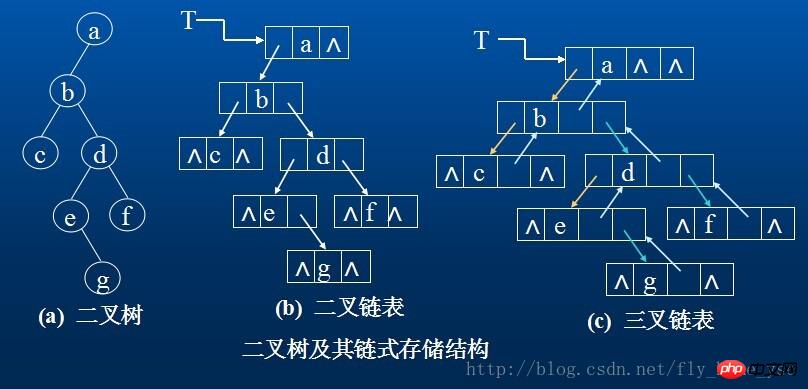
2. Linked storage structure
The node of a binary tree consists of a data element and two branches pointing to its left and right subtrees respectively, which means that the nodes in the linked list of the binary tree contain at least three fields. : Data field and left and right pointer fields. Sometimes, in order to facilitate finding the parents of a node, a pointer field pointing to its parent node can be added to the node structure. The storage structures of binary trees obtained by using these two structures are called binary linked lists and triple linked lists respectively.
There are n+1 empty link fields in a binary linked list containing n nodes. We can use these empty link fields to store other useful information, thereby obtaining another linked storage structure-clue linked list.

There are three main types of binary tree traversal:

First (root) order traversal: root left and right
Middle (root) order traversal: left root right
Back (root) order Traversal: Left and right roots

Sequential storage structure of binary tree:

Chained storage form of binary tree:

// 顺序存储结构
    var tree = [1, 2, 3, 4, 5, , 6, , , 7];
    // 链式存储结构
    function BinaryTree(data, leftChild, rightChild) {
        this.data = data || null;
        // 左右孩子结点
        this.leftChild = leftChild || null;
        this.rightChild = rightChild || null;
    }

Traversing Binary Tree: refers to visiting each node in the binary tree once and only once according to the specified rules.

1. Preorder traversal of the binary tree

1) The recursive definition of the algorithm is:

If the binary tree is empty, the traversal ends; otherwise

　⑴ Access Root node;

　⑵Traverse the left subtree in order (call this algorithm recursively);

　⑶Traverse the right subtree in order (call this algorithm recursively).

Algorithm implementation:

// 顺序存储结构的递归先序遍历
    var tree = [1, 2, 3, 4, 5, , 6, , , 7];    console.log('preOrder:');
    void function preOrderTraverse(x, visit) {
        visit(tree[x]);
        if (tree[2 * x + 1]) preOrderTraverse(2 * x + 1, visit);
        if (tree[2 * x + 2]) preOrderTraverse(2 * x + 2, visit);
    }(0, function (value) {
        console.log(value);
    });
    // 链式存储结构的递归先序遍历
    BinaryTree.prototype.preOrderTraverse = function preOrderTraverse(visit) {
        visit(this.data);
        if (this.leftChild) preOrderTraverse.call(this.leftChild, visit);
        if (this.rightChild) preOrderTraverse.call(this.rightChild, visit);
    };

2) Non-recursive algorithm:

Assume T is a variable pointing to the root node of the binary tree, the non-recursive algorithm is: If the binary tree is empty, then Return; otherwise, let p=T;

　(1) p is the root node;

　(2) If p is not empty or the stack is not empty;

(3) If p is not empty, access the node pointed by p, push p onto the stack, p = p.leftChild, access the left subtree;

　 (4) Otherwise; pop back to p, then p = p.rightChild, access the right subtree

　(5) Go to (2) until the stack is empty.

Code implementation:

// 链式存储的非递归先序遍历

    // 方法1
    BinaryTree.prototype.preOrder_stack = function (visit) {        
    var stack = new Stack();        
    stack.push(this);        
    while (stack.top) {            
    var p;            // 向左走到尽头
            while ((p = stack.peek())) {
                p.data && visit(p.data);                
                stack.push(p.leftChild);
            }            
            stack.pop();            
            if (stack.top) {
                p = stack.pop();                
                stack.push(p.rightChild);
            }
        }
    };    // 方法2
     BinaryTree.prototype.preOrder_stack2 = function (visit) {        
     var stack = new Stack();        
     var p = this;        
     while (p || stack.top) {            
     if (p) {                
     stack.push(p);
                p.data && visit(p.data);
                p = p.leftChild;
            } else {
                p = stack.pop();
                p = p.rightChild;
            }
        }
    };

2. In-order traversal of the binary tree:

1) The recursive definition of the algorithm is:

If the binary tree is empty, then traverse End; otherwise

　⑴ In-order traverse the left subtree (recursively call this algorithm);

　⑵ Visit the root node; call this algorithm).

// 顺序存储结构的递归中序遍历
    var tree = [1, 2, 3, 4, 5, , 6, , , 7];    
    console.log('inOrder:');
    void function inOrderTraverse(x, visit) {        
    if (tree[2 * x + 1]) inOrderTraverse(2 * x + 1, visit);
        visit(tree[x]);
        if (tree[2 * x + 2]) inOrderTraverse(2 * x + 2, visit);
    }(0, function (value) {
        console.log(value);
    });

    // 链式存储的递归中序遍历
    BinaryTree.prototype.inPrderTraverse = function inPrderTraverse(visit) {        
    if (this.leftChild) inPrderTraverse.call(this.leftChild, visit);
        visit(this.data);
        if (this.rightChild) inPrderTraverse.call(this.rightChild, visit);
    };

2) Non-recursive algorithm

T is a variable pointing to the root node of the binary tree. The non-recursive algorithm is: If the binary tree is empty, return; otherwise, let p=T

　⑴ If p is not empty, p is pushed onto the stack, p=p.leftChild;

<br/>

　⑵ Otherwise (that is, p is empty), push back to p and access the node pointed by p, p =p.rightChild;

　⑶ Go to (1);

Until the stack is empty.

　

// 方法1
    inOrder_stack1: function (visit) {        
    var stack = new Stack();        
    stack.push(this);        
    while (stack.top) {            
    var p;            // 向左走到尽头
            while ((p = stack.peek())) {                
            stack.push(p.leftChild);
            }            
            stack.pop();            
            if (stack.top) {
                p = stack.pop();
                p.data && visit(p.data);                
                stack.push(p.rightChild);
            }
        }
    },    // 方法2
    inOrder_stack2: function (visit) {        
    var stack = new Stack();        
    var p = this;        
    while (p || stack.top) {            
    if (p) {                
    stack.push(p);
                p = p.leftChild;
            } else {
                p = stack.pop();
                p.data && visit(p.data);
                p = p.rightChild;
            }
        }
    },

<br/>3. Post-order traversal of the binary tree:

1) Recursive algorithm

If the binary tree is empty, the traversal ends; otherwise

　⑴ Post-order traversal of the left subtree (recursively calling this algorithm);

　⑵ Post-order traversal of the right subtree (recursive call of this algorithm);

　⑶ Visit the root node.

// 顺序存储结构的递归后序遍历
    var tree = [1, 2, 3, 4, 5, , 6, , , 7];    
    console.log('postOrder:');
    void function postOrderTraverse(x, visit) {        
    if (tree[2 * x + 1]) postOrderTraverse(2 * x + 1, visit);
        if (tree[2 * x + 2]) postOrderTraverse(2 * x + 2, visit);
        visit(tree[x]);
    }(0, function (value) {
        console.log(value);
    });
    // 链式存储的递归后序遍历
    BinaryTree.prototype.postOrderTraverse = function postOrderTraverse(visit) {        
    if (this.leftChild) postOrderTraverse.call(this.leftChild, visit);
        if (this.rightChild) postOrderTraverse.call(this.rightChild, visit);
        visit(this.data);
    };

<br/>2) Non-recursive algorithm

In post-order traversal, the root node is the last one visited. Therefore, during the traversal process, when the search pointer points to a certain root node, it cannot be accessed immediately, but its left subtree must be traversed first, and the root node is pushed onto the stack. When the root node is searched after traversing its left subtree, it is still inaccessible, and its right subtree needs to be traversed. Therefore, the root node needs to be pushed onto the stack again. When its right subtree is traversed and then popped back onto the stack, it can be accessed. Therefore, set up a status flag variable mark:

mark=0 means that this node has just been accessed, mark=1 means that the left subtree processing is completed and returned,

mark=2 means that the right subtree is processed End return. Each time the action is decided based on the mark field on the top of the stack

Algorithm implementation idea:

　(1) The root node is pushed into the stack, and mark = 0;

　(2 ) If the stack is not empty, pop it to the node;

　(3) If the mark of the node = 0, modify the mark of the current node to 1, and push the left subtree onto the stack;

　(4 ) If the mark of the node = 1, modify the mark of the current node to 2, and push the right subtree onto the stack;

　　(5) If the mark of the node = 2, access the value of the current node node;

　(6) End until the stack is empty.

　

postOrder_stack: function (visit) {
        var stack = new Stack();        
        stack.push([this, 0]);        
        while (stack.top) {
            var a = stack.pop();
            var node = a[0];            
            switch (a[1]) {                
            case 0:                    
            stack.push([node, 1]);  // 修改mark域
                    if (node.leftChild) stack.push([node.leftChild, 0]);  // 访问左子树
                    break;                
                    case 1:                    
                    stack.push([node, 2]);                    
                    if (node.rightChild) stack.push([node.rightChild, 0]);                    
                    break;                
                    case 2:
                    node.data && visit(node.data);                    
                    break;                
                    default:                    
                    break;
            }
        }
    }

<br/>A specific example

<html>
  <head>
    <meta charset="utf-8">
    <title>文档标题</title>
    <meta http-equiv="X-UA-Compatible" content="IE=edge,chrome=1" />
    <meta name="renderer" content="webkit">
    <meta name="keywords" content="your keywords">
    <meta name="description" content="your description">
    <link rel="shortcut icon" type="image/ico" href="/favicon.ico" />
    <meta name="viewport" content="width=device-width, initial-scale=1.0"></head><body>
    <p class="container"></p>
    <script>
   // 顺序存储结构
   (function () {
       // 顺序存储结构的遍历
       var tree = ["a","b","c","d","e","f","g"];

       console.log(&#39;preOrder:&#39;);
       +function preOrderTraverse(x, visit) {
           visit(tree[x]);           
           if (tree[2 * x + 1]) preOrderTraverse(2 * x + 1, visit);           
           if (tree[2 * x + 2]) preOrderTraverse(2 * x + 2, visit);
       }(0, function (value) {
           console.log(value);
       });

       console.log(&#39;inOrder:&#39;);       
       void function inOrderTraverse(x, visit) {
           if (tree[2 * x + 1]) inOrderTraverse(2 * x + 1, visit);
           visit(tree[x]);          
           if (tree[2 * x + 2]) inOrderTraverse(2 * x + 2, visit);
       }(0, function (value) {
           console.log(value);
       });

       console.log(&#39;postOrder:&#39;);       
       void function postOrderTraverse(x, visit) {
           if (tree[2 * x + 1]) postOrderTraverse(2 * x + 1, visit);           
           if (tree[2 * x + 2]) postOrderTraverse(2 * x + 2, visit);
           visit(tree[x]);
       }(0, function (value) {
           console.log(value);
       });
   }());   // 求从tree到node结点路径的递归算法
   function findPath(tree, node, path, i) {
       var found = false;       
       void function recurse(tree, i) {
           if (tree == node) {
               found = true;              
               return;
           }

           path[i] = tree;           
           if (tree.leftChild) recurse(tree.leftChild, i + 1);           
           if (tree.rightChild && !found) recurse(tree.rightChild, i + 1);           
           if (!found) path[i] = null;
       }(tree, i);
   }   var global = Function(&#39;return this;&#39;)();    
   </script>
 </body>
</html>

The above is the detailed content of js implements data structure: tree and binary tree, binary tree traversal and basic operation methods. For more information, please follow other related articles on the PHP Chinese website!