Detailed explanation of bubble sorting method
Bubble sorting method
HTML5 Academy-Coder: This issue continues to introduce the algorithm - bubble sorting method. The bubble sort algorithm is relatively simple, easy to use, and relatively stable. It is a relatively easy-to-understand algorithm and one of the algorithms that interviewers frequently ask questions about.
Tips: The basic knowledge of "algorithm" and "sorting" has been explained in detail in the previous "Selection Sorting Method". You can click on the relevant article link at the end of the article to view it, and I will not repeat it here.
Principle of Bubble Sorting
Basic Principle
Traverse from the head of the sequence, compare them two by two, if the former is larger than the latter, swap positions until the end Swap the largest number (the largest number in this sorting) to the end of the unordered sequence, thereby becoming part of the ordered sequence;
During the next traversal, the maximum number after each previous traversal will no longer participate. Sorting;
Repeat this operation multiple times until the sequence sorting is completed.
Because in the sorting process, decimals are always placed forward and large numbers are placed backward, similar to bubbles gradually floating upward, so it is called bubble sorting.
Principle Illustration
Tips: Blue represents waiting for exchange in a round of sorting, black represents exchange completed in this round of sorting, red represents sorting completed
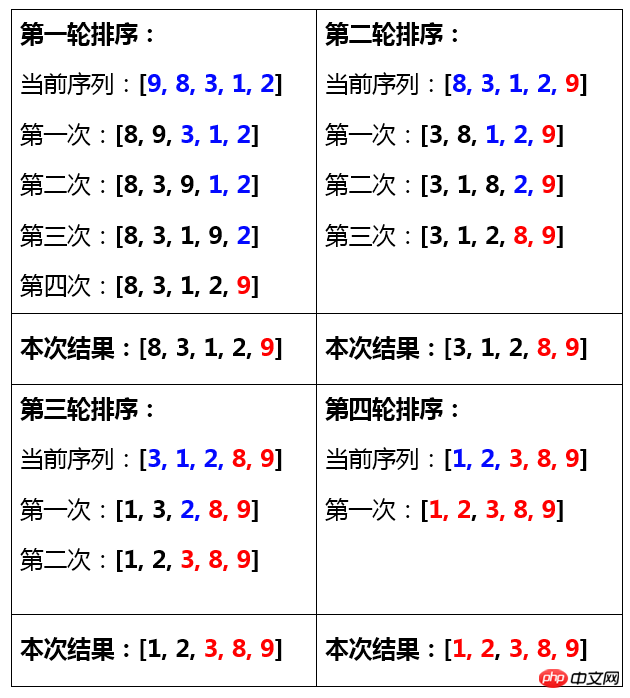
Decomposition of steps to achieve bubbling
Use a for loop to determine the number of sorting
Since the sequence to be sorted can already be determined when there is only one number left, there is no need Sort, therefore, the number of sorting is sequence length – 1.

Control the number of comparisons for each sorting
Every time you sort, multiple numbers in the sequence must be compared in pairs, and multiple comparisons are required Use the for statement to achieve this. This for loop is nested in the for loop of sorted times (forming a nest of double for).

Tips: j needs to be set to less than len - i - 1. The reason for subtracting i is that the sorted numbers no longer participate in the comparison. The reason for subtracting 1 is that the array Index values start from 0.
Core function - compare pairs and exchange positions according to the situation
Compare the size of the two numbers. If the former is larger than the latter, exchange the values, that is, exchange the positions.

Full code of bubble sorting method

Optimization of bubble sorting method
If the sequence The data is: [0, 1, 2, 3, 4, 5];
Use the above bubble sorting method to sort, and the result will definitely be fine, but the sequence to be sorted is in order Yes, theoretically there is no need to traverse sorting.
The current algorithm will perform traversal sorting regardless of whether the initial sequence is in order, and the efficiency will be relatively low, so the current sorting algorithm needs to be optimized.
In the following algorithm, a swap variable is introduced and initialized to false before each sorting; if two numbers exchange positions, set it to true.
At the end of each sorting, determine whether swap is false. If so, it means that the sequence has been sorted or the sequence itself is an ordered sequence, and the next sorting will not be performed.
Through this method, unnecessary comparisons and position exchanges are reduced, and the performance of the algorithm is further improved.

Efficiency of bubble sorting method
Time complexity
The best state: the sequence to be sorted itself is an ordered sequence, According to the optimized code, it can be concluded that the number of sorting is n-1 times, and the time complexity is O(n);
Worst case scenario: the sequence to be sorted is in reverse order, and 1 needs to be sorted at this time + 2 +3...(n - 1) = n(n - 1)/2 times
The time complexity is O(n^2).
Space complexity
The bubble sort method requires an extra space (temp variable) to exchange the position of elements, so the space complexity is O(1).
Stability of the algorithm
When adjacent elements are equal, there is no need to exchange positions, and the order of the same elements will not change. Therefore, it is a stable sorting.
What is O? !
Time complexity, more accurately, describes the time growth curve of an algorithm as the size of the problem continues to increase. Therefore, these orders of magnitude increase are not an accurate performance evaluation and can be understood as an approximation. (Similar to space complexity)
O(n?) means that when n is large enough, the complexity is approximately equal to Cn?, C is a certain constant. Simply put, when n is large enough, then As n grows linearly the complexity will grow squarely.
O(n) means that when n is very large, the complexity is approximately equal to Cn, and C is a certain constant. In short: as n grows linearly, the complexity grows along a linear scale.
O(1) means that when n is very large, the complexity basically does not increase. In short: as n grows linearly, the complexity is not affected by n and grows along a constant level (the constant here is 1).
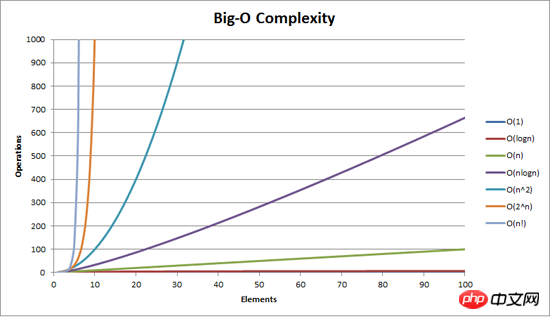
Tips: In the picture, O(1) is close to the X-axis and cannot be seen clearly.
Tips: This picture comes from the "Stack Overflow" website.
Related article links
Selection sorting method
Happy every day
Life is hard and coding is not easy, but don’t forget to smile!

The above is the detailed content of Detailed explanation of bubble sorting method. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1382
1382
 52
52
 How to sort photos by date taken in Windows 11/10
Feb 19, 2024 pm 08:45 PM
How to sort photos by date taken in Windows 11/10
Feb 19, 2024 pm 08:45 PM
This article will introduce how to sort pictures according to shooting date in Windows 11/10, and also discuss what to do if Windows does not sort pictures by date. In Windows systems, organizing photos properly is crucial to making it easy to find image files. Users can manage folders containing photos based on different sorting methods such as date, size, and name. In addition, you can set ascending or descending order as needed to organize files more flexibly. How to Sort Photos by Date Taken in Windows 11/10 To sort photos by date taken in Windows, follow these steps: Open Pictures, Desktop, or any folder where you place photos In the Ribbon menu, click
 How to sort emails by sender, subject, date, category, size in Outlook
Feb 19, 2024 am 10:48 AM
How to sort emails by sender, subject, date, category, size in Outlook
Feb 19, 2024 am 10:48 AM
Outlook offers many settings and features to help you manage your work more efficiently. One of them is the sorting option that allows you to categorize your emails according to your needs. In this tutorial, we will learn how to use Outlook's sorting feature to organize emails based on criteria such as sender, subject, date, category, or size. This will make it easier for you to process and find important information, making you more productive. Microsoft Outlook is a powerful application that makes it easy to centrally manage your email and calendar schedules. You can easily send, receive, and organize email, while built-in calendar functionality makes it easy to keep track of your upcoming events and appointments. How to be in Outloo
 Detailed explanation of obtaining administrator rights in Win11
Mar 08, 2024 pm 03:06 PM
Detailed explanation of obtaining administrator rights in Win11
Mar 08, 2024 pm 03:06 PM
Windows operating system is one of the most popular operating systems in the world, and its new version Win11 has attracted much attention. In the Win11 system, obtaining administrator rights is an important operation. Administrator rights allow users to perform more operations and settings on the system. This article will introduce in detail how to obtain administrator permissions in Win11 system and how to effectively manage permissions. In the Win11 system, administrator rights are divided into two types: local administrator and domain administrator. A local administrator has full administrative rights to the local computer
 Detailed explanation of division operation in Oracle SQL
Mar 10, 2024 am 09:51 AM
Detailed explanation of division operation in Oracle SQL
Mar 10, 2024 am 09:51 AM
Detailed explanation of division operation in OracleSQL In OracleSQL, division operation is a common and important mathematical operation, used to calculate the result of dividing two numbers. Division is often used in database queries, so understanding the division operation and its usage in OracleSQL is one of the essential skills for database developers. This article will discuss the relevant knowledge of division operations in OracleSQL in detail and provide specific code examples for readers' reference. 1. Division operation in OracleSQL
 How to sort WPS scores
Mar 20, 2024 am 11:28 AM
How to sort WPS scores
Mar 20, 2024 am 11:28 AM
In our work, we often use wps software. There are many ways to process data in wps software, and the functions are also very powerful. We often use functions to find averages, summaries, etc. It can be said that as long as The methods that can be used for statistical data have been prepared for everyone in the WPS software library. Below we will introduce the steps of how to sort the scores in WPS. After reading this, you can learn from the experience. 1. First open the table that needs to be ranked. As shown below. 2. Then enter the formula =rank(B2, B2: B5, 0), and be sure to enter 0. As shown below. 3. After entering the formula, press the F4 key on the computer keyboard. This step is to change the relative reference into an absolute reference.
 Detailed explanation of the role and usage of PHP modulo operator
Mar 19, 2024 pm 04:33 PM
Detailed explanation of the role and usage of PHP modulo operator
Mar 19, 2024 pm 04:33 PM
The modulo operator (%) in PHP is used to obtain the remainder of the division of two numbers. In this article, we will discuss the role and usage of the modulo operator in detail, and provide specific code examples to help readers better understand. 1. The role of the modulo operator In mathematics, when we divide an integer by another integer, we get a quotient and a remainder. For example, when we divide 10 by 3, the quotient is 3 and the remainder is 1. The modulo operator is used to obtain this remainder. 2. Usage of the modulo operator In PHP, use the % symbol to represent the modulus
 Detailed explanation of the linux system call system() function
Feb 22, 2024 pm 08:21 PM
Detailed explanation of the linux system call system() function
Feb 22, 2024 pm 08:21 PM
Detailed explanation of Linux system call system() function System call is a very important part of the Linux operating system. It provides a way to interact with the system kernel. Among them, the system() function is one of the commonly used system call functions. This article will introduce the use of the system() function in detail and provide corresponding code examples. Basic Concepts of System Calls System calls are a way for user programs to interact with the operating system kernel. User programs request the operating system by calling system call functions
 Detailed explanation of Linux curl command
Feb 21, 2024 pm 10:33 PM
Detailed explanation of Linux curl command
Feb 21, 2024 pm 10:33 PM
Detailed explanation of Linux's curl command Summary: curl is a powerful command line tool used for data communication with the server. This article will introduce the basic usage of the curl command and provide actual code examples to help readers better understand and apply the command. 1. What is curl? curl is a command line tool used to send and receive various network requests. It supports multiple protocols, such as HTTP, FTP, TELNET, etc., and provides rich functions, such as file upload, file download, data transmission, proxy




