How to implement quick sort
Quick Sorting Method
HTML5 Academy-Coder: In the previous issues of "Algorithm Journey", I shared with you the bubble sorting method and the selection sorting method. They both have a time complexity of O(n^ 2) "Slow" sorting. Today I would like to share with you the most widely used and fast sorting algorithm among various sorting algorithms - quick sort [average time complexity is O (n logn)].
Tips 1: The basic knowledge of "algorithm" and "sorting" has been explained in detail in the previous "Selection Sorting Method". You can click on the relevant article link at the end of the article to view it, and I will not repeat it here.
Tips 2: If there is no special instructions, the quick sort in this article is sorted from small to large.
Principle of quick sort
Quick sort is a partition and exchange sort. It adopts the divide-and-conquer strategy, which is usually called the divide-and-conquer method.
Divide and Conquer Method
Basic idea: Decompose the original problem into several smaller sub-problems but similar structures to the original problem. Solve these subproblems recursively, and then combine the results of these subproblems into the results of the original problem.
Basic Principle
Select any number from the sequence as the "base";
All numbers smaller than the "base" are moved to the left of the "base"; all Numbers greater than or equal to the "baseline" are moved to the right of the "baseline";
After this move is completed, the "baseline" will be in the middle of the two sequences and will no longer participate in subsequent sorting;
Repeat the above steps for the two subsequences to the left and right of the "baseline" until only one number remains in all subsequences.
Principle Illustration
The existing sequence is [8, 4, 7, 2, 0, 3, 1]. The following demonstrates how to sort it using the quick sort method.

Step breakdown to implement quick sort
Select "baseline" and separate it from the original array
Get the index of the baseline first value, and then use the splice array method to get the benchmark value.

Tips: In this example, the index value of the benchmark = parseInt (sequence length / 2)
Tips: The splice method will change the original array. For example, arr = [1, 2, 3]; The base index value is 1, the base value is 2, and the original array becomes arr = [1, 3];
Traverse the sequence and split the sequence
Compare the size with the "baseline" and split it into two subsequences
Numbers smaller than the "baseline" are stored in the leftArr array, and numbers greater than or equal to the "baseline" are stored in the rightArr array

#Tips: Of course, you can also store the number less than or equal to the "baseline" in leftArr, and the number greater than the "baseline" in rightArr
Since the sequence needs to be traversed, Compare each number with the "baseline", so you need to use the for statement to implement

recursive call, traverse the subsequence and combine the results of the subsequence
Define a function whose formal parameters are used to receive arrays
function quickSort(arr) { };
Implement recursive call traversal Sequence, use the concat array method to combine the results of the subsequence

Judge the length of the subsequence
During the recursive call, when the length of the subsequence is equal to 1 , then stop the recursive call and return the current array.

Complete code of quick sort method

Efficiency of quick sort method
Time complexity
Worst case scenario: The "baseline" selected each time is the smallest number/the largest number in the sequence. This situation is similar to the bubble sorting method (only one number [baseline number] can be determined at a time order), the time complexity is O(n^2)
Best case: the "baseline" selected each time is the middle number in the sequence (it is the median, not the position) middle), then the current sequence is divided into two subsequences of equal length each time. At this time, the first time there are two subsequences n/2 and n/2, the second time there are four subsequences n/4, n/4, n/4, n/4, and so on, n numbers It takes a total of logn times to complete the sorting (2^x=n, x=logn), and each time it has a complexity of n, the time complexity is O(n logn)
Space complexity
Worst case: n-1 recursive calls are required, and its space complexity is O(n)
Best case: logn recursive calls are required, and its space complexity is O(logn )
Stability of the algorithm
Quick sort is an unstable sorting algorithm
For example: the existing sequence is [1, 0, 1, 3], and the "baseline" number selection is After the first round of comparison, the second 1
becomes [0, 1, 1, 3], the left sequence is [0], and the right sequence is [1, 3] (1 in the right sequence It is the first one before 1)
It is not difficult to find that the order of the two 1's in the original sequence has been destroyed, and the order has been changed, which is naturally an "unstable" sorting algorithm
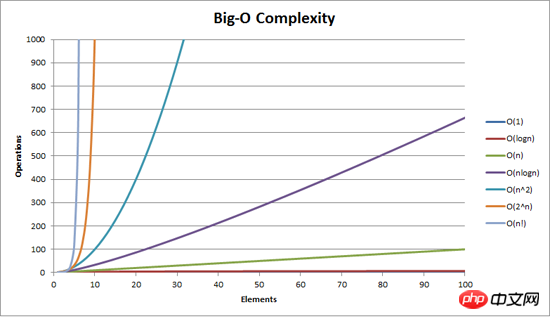
About O
In the previous article "Bubble Sorting Method", we explained in detail what O is, so I won't say more here, just go to the picture
The above is the detailed content of How to implement quick sort. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1385
1385
 52
52
 How to write a novel in the Tomato Free Novel app. Share the tutorial on how to write a novel in Tomato Novel.
Mar 28, 2024 pm 12:50 PM
How to write a novel in the Tomato Free Novel app. Share the tutorial on how to write a novel in Tomato Novel.
Mar 28, 2024 pm 12:50 PM
Tomato Novel is a very popular novel reading software. We often have new novels and comics to read in Tomato Novel. Every novel and comic is very interesting. Many friends also want to write novels. Earn pocket money and edit the content of the novel you want to write into text. So how do we write the novel in it? My friends don’t know, so let’s go to this site together. Let’s take some time to look at an introduction to how to write a novel. Share the Tomato novel tutorial on how to write a novel. 1. First open the Tomato free novel app on your mobile phone and click on Personal Center - Writer Center. 2. Jump to the Tomato Writer Assistant page - click on Create a new book at the end of the novel.
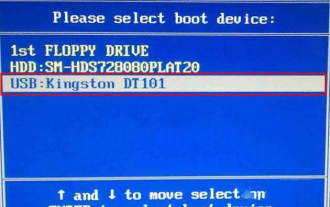 How to enter bios on Colorful motherboard? Teach you two methods
Mar 13, 2024 pm 06:01 PM
How to enter bios on Colorful motherboard? Teach you two methods
Mar 13, 2024 pm 06:01 PM
Colorful motherboards enjoy high popularity and market share in the Chinese domestic market, but some users of Colorful motherboards still don’t know how to enter the bios for settings? In response to this situation, the editor has specially brought you two methods to enter the colorful motherboard bios. Come and try it! Method 1: Use the U disk startup shortcut key to directly enter the U disk installation system. The shortcut key for the Colorful motherboard to start the U disk with one click is ESC or F11. First, use Black Shark Installation Master to create a Black Shark U disk boot disk, and then turn on the computer. When you see the startup screen, continuously press the ESC or F11 key on the keyboard to enter a window for sequential selection of startup items. Move the cursor to the place where "USB" is displayed, and then
 How to recover deleted contacts on WeChat (simple tutorial tells you how to recover deleted contacts)
May 01, 2024 pm 12:01 PM
How to recover deleted contacts on WeChat (simple tutorial tells you how to recover deleted contacts)
May 01, 2024 pm 12:01 PM
Unfortunately, people often delete certain contacts accidentally for some reasons. WeChat is a widely used social software. To help users solve this problem, this article will introduce how to retrieve deleted contacts in a simple way. 1. Understand the WeChat contact deletion mechanism. This provides us with the possibility to retrieve deleted contacts. The contact deletion mechanism in WeChat removes them from the address book, but does not delete them completely. 2. Use WeChat’s built-in “Contact Book Recovery” function. WeChat provides “Contact Book Recovery” to save time and energy. Users can quickly retrieve previously deleted contacts through this function. 3. Enter the WeChat settings page and click the lower right corner, open the WeChat application "Me" and click the settings icon in the upper right corner to enter the settings page.
 How to set font size on mobile phone (easily adjust font size on mobile phone)
May 07, 2024 pm 03:34 PM
How to set font size on mobile phone (easily adjust font size on mobile phone)
May 07, 2024 pm 03:34 PM
Setting font size has become an important personalization requirement as mobile phones become an important tool in people's daily lives. In order to meet the needs of different users, this article will introduce how to improve the mobile phone use experience and adjust the font size of the mobile phone through simple operations. Why do you need to adjust the font size of your mobile phone - Adjusting the font size can make the text clearer and easier to read - Suitable for the reading needs of users of different ages - Convenient for users with poor vision to use the font size setting function of the mobile phone system - How to enter the system settings interface - In Find and enter the "Display" option in the settings interface - find the "Font Size" option and adjust it. Adjust the font size with a third-party application - download and install an application that supports font size adjustment - open the application and enter the relevant settings interface - according to the individual
 The secret of hatching mobile dragon eggs is revealed (step by step to teach you how to successfully hatch mobile dragon eggs)
May 04, 2024 pm 06:01 PM
The secret of hatching mobile dragon eggs is revealed (step by step to teach you how to successfully hatch mobile dragon eggs)
May 04, 2024 pm 06:01 PM
Mobile games have become an integral part of people's lives with the development of technology. It has attracted the attention of many players with its cute dragon egg image and interesting hatching process, and one of the games that has attracted much attention is the mobile version of Dragon Egg. To help players better cultivate and grow their own dragons in the game, this article will introduce to you how to hatch dragon eggs in the mobile version. 1. Choose the appropriate type of dragon egg. Players need to carefully choose the type of dragon egg that they like and suit themselves, based on the different types of dragon egg attributes and abilities provided in the game. 2. Upgrade the level of the incubation machine. Players need to improve the level of the incubation machine by completing tasks and collecting props. The level of the incubation machine determines the hatching speed and hatching success rate. 3. Collect the resources required for hatching. Players need to be in the game
 Quickly master: How to open two WeChat accounts on Huawei mobile phones revealed!
Mar 23, 2024 am 10:42 AM
Quickly master: How to open two WeChat accounts on Huawei mobile phones revealed!
Mar 23, 2024 am 10:42 AM
In today's society, mobile phones have become an indispensable part of our lives. As an important tool for our daily communication, work, and life, WeChat is often used. However, it may be necessary to separate two WeChat accounts when handling different transactions, which requires the mobile phone to support logging in to two WeChat accounts at the same time. As a well-known domestic brand, Huawei mobile phones are used by many people. So what is the method to open two WeChat accounts on Huawei mobile phones? Let’s reveal the secret of this method. First of all, you need to use two WeChat accounts at the same time on your Huawei mobile phone. The easiest way is to
 The difference between Go language methods and functions and analysis of application scenarios
Apr 04, 2024 am 09:24 AM
The difference between Go language methods and functions and analysis of application scenarios
Apr 04, 2024 am 09:24 AM
The difference between Go language methods and functions lies in their association with structures: methods are associated with structures and are used to operate structure data or methods; functions are independent of types and are used to perform general operations.
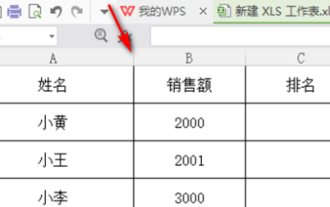 How to sort WPS scores
Mar 20, 2024 am 11:28 AM
How to sort WPS scores
Mar 20, 2024 am 11:28 AM
In our work, we often use wps software. There are many ways to process data in wps software, and the functions are also very powerful. We often use functions to find averages, summaries, etc. It can be said that as long as The methods that can be used for statistical data have been prepared for everyone in the WPS software library. Below we will introduce the steps of how to sort the scores in WPS. After reading this, you can learn from the experience. 1. First open the table that needs to be ranked. As shown below. 2. Then enter the formula =rank(B2, B2: B5, 0), and be sure to enter 0. As shown below. 3. After entering the formula, press the F4 key on the computer keyboard. This step is to change the relative reference into an absolute reference.




