
Why is 0.1 + 0.2 not equal to 0.3? (Correct result: 0.30000000000000004)
Why is 0.8 * 7 not equal to 5.6? (Correct result: 5.6000000000000005)
var_dump(intval(0.58 * 100));
The correct result is 57, not 58
Actually, these results are not language bugs, but are related to the implementation principle of the language. All numbers in js are unified as Number, including integers, which are actually all double precision (double) types.
And PHP will distinguish between int and float. No matter what language, as long as floating point operations are involved, there are similar problems, so you must pay attention when using them.
According to the international standard IEEE 754, any binary floating point number V can be expressed in the following form:
V = (-1)s * M * E 1. (-1)s 表示符号位,当s=0,V为正数;当s=1,V为负数。 2. M表示有效数字,大于等于1,小于2。 3. 2E 表示指数位。
For example: decimal -5.0 , written in binary is -101.0, which is equivalent to -1.01×22. Then, s=1, M=1.01, E=2.
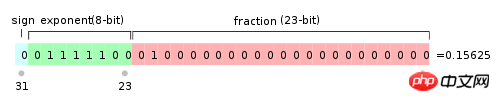
IEEE 754 stipulates that for a 32-bit floating point number, the highest 1 bit is the sign bit s, the next 8 bits are the exponent E, and the remaining 23 bits are the significant digit M.
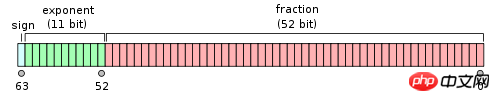
For a 64-bit floating point number, the highest 1 bit is the sign bit S, the next 11 bits are the exponent E, and the remaining 52 bits are the significant digit M.
IEEE 754 also has some special provisions for the significant digit M and the exponent E.
As mentioned before, 1≤M<2, that is to say, M can be written in the form of 1.xxxxxx, where xxxxxx represents the decimal part. IEEE 754 stipulates that when M is stored inside the computer, the first digit of this number is always 1 by default, so it can be discarded and only the following xxxxxx parts are saved. For example, when saving 1.01, only 01 is saved, and when reading, the first 1 is added. The purpose of this is to save 1 significant figure. Taking a 32-bit floating point number as an example, there are only 23 bits left for M. After the first 1 is rounded off, 24 significant digits can be saved.
As for the index E, the situation is more complicated.
First of all, E is an unsigned integer (unsigned int). This means that if E is 8 bits, its value range is 0~255; if E is 11 bits, its value range is 0~2047. However, we know that E in scientific notation can be a negative number, so IEEE 754 stipulates that the real value of E must be subtracted from E by an intermediate number. For an 8-bit E, this intermediate number is 127; for 11 The middle number is 1023.
For example, the E of 210 is 10, so when it is saved as a 32-bit floating point number, it must be saved as 10 (the real value of E) + 127 = 137 (E), which is 10001001.
Then, the index E can be further divided into three situations:
(1) E is not all 0 or not all 1. At this time, the floating point number is represented by the above rules, that is, the calculated value of the exponent E is subtracted from 127 (or 1023) to obtain the real value, and then the first 1 is added before the significant digit M.
(2)E is all 0. At this time, the exponent E of the floating point number is equal to 1-127 (or 1-1023), and the effective digit M no longer adds the first 1, but is reduced to a decimal of 0.xxxxxx. This is done to represent ±0, and very small numbers close to 0.
(3)E is all 1. At this time, if the significant digits M are all 0, it means ± infinity (the sign bit depends on the sign bit s); if the significant digits M are not all 0, it means that the number is not a number (NaN). >
The above is the detailed content of Analysis of the pitfalls of PHP and JS floating point operations. For more information, please follow other related articles on the PHP Chinese website!




