 Web Front-end
Web Front-end
 JS Tutorial
JS Tutorial
 Dynamic programming example analysis of JavaScript advanced algorithms
Dynamic programming example analysis of JavaScript advanced algorithms
Dynamic programming example analysis of JavaScript advanced algorithms
In fact, in our front-end development, there are not many advanced algorithms used. In most cases, if statements, for statements, switch statements, etc. can be solved. If it's a little more complicated, you might think of using recursion to solve it. This article mainly introduces the dynamic programming of advanced JavaScript programming algorithms, and analyzes the principles, implementation techniques and related usage precautions of the JavaScript dynamic programming algorithm in the form of examples. Friends in need can refer to it.
But it should be noted that recursion is simple to write, but its actual execution efficiency is not high.
Let’s take a look at the dynamic programming algorithm:
Dynamic programming solution starts from the bottom to solve the problem, solves all the small problems, and then merges them into an overall solution to solve the entire problem. Big problem.
Example (Calculating Fibonacci Sequence)
The Fibonacci Sequence refers to a sequence of 1, 1, 2, 3, 5, 8, 13, 21, 34 , 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368...
This sequence starts from the 3rd item Initially, each term is equal to the sum of the previous two terms.
For this sequence, you can use a recursive function to calculate the nth value
// 斐波那契数列
function recurFib(n) {
if(n < 2){
return n ;
}else {
// document.write("第"+(n-1)+"次计算 n-1="+(n-1)+recurFib(n-1)+' ');
// document.write("n-2="+(n-2)+recurFib(n-2)+"<br>");
return recurFib(n-1)+recurFib(n-2)
}
}It is indeed a very The concise code, with the commented code above, is used to print out how many times the function needs to be executed when n =. However, a discerning person can see at a glance that the number of executions will increase horribly as n increases. .
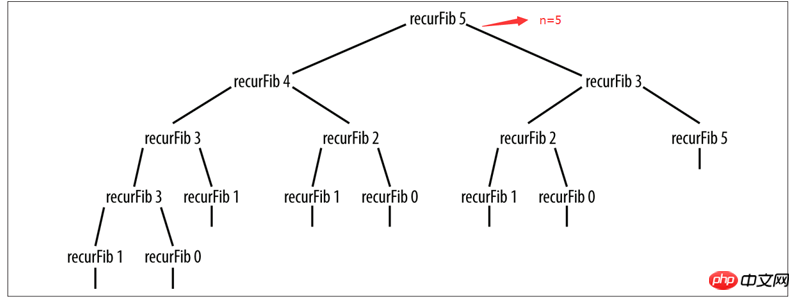
When n=5, the recursion tree has grown very big... It can be predicted that when n=10, or even n=100...
Understanding the difference in execution efficiency of recursive functions, let’s look at how dynamic programming is done
function dynFib(n) {
let val = [];
for(let i = 0; i <= n; ++i){
val[i]=0;
}
if(n ===1 || n === 2){
return 1;
}
else {
val[1] =1;
val[2] = 2;
for(let i = 3; i <= n; ++i){
val[i] = val [i-1] +val[i-2] ;
}
}
return val[n-1]
}Through the array val The intermediate result is saved in . If the Fibonacci number to be calculated is 1 or 2, then the if statement will return 1. Otherwise, the values 1 and 2 will be stored at positions 1 and 2 in the val array.
The loop will traverse from 3 to the input parameters, and assign each element of the array to the sum of the first two elements. The loop ends, and the last element value of the array is the final calculated value. Fibonacci value, this value will also be used as the return value of the function.
Next, you can write a simple test function to compare the running time of the two.
// 定义一个测试函数,将待测函数作为参数传入
function test(func,n){
let start = new Date().getTime();//起始时间
let res = func(n);//执行待测函数
document.write('<br>'+'当n='+n+'的时候 '+res+'<br>');
let end = new Date().getTime();//结束时间
return (end - start)+"ms";//返回函数执行需要时间
}Print function execution
let time = test(recurFib,40); document.write(time); let time2 = test(dynFib,40); document.write(time2);
The results are as follows:

Finally, you may have realized that when using an iterative scheme to calculate the Fibonacci sequence, you do not need to use an array.
The reason why arrays are needed is because dynamic programming algorithms usually need to save intermediate results.
The following is the iterative version of the Fibonacci function definition
function iterFib(n) {
let last = 1;
let nextLast = 1;
let result = 1;
for (let i = 2; i < n; ++i) {
result = last + nextLast;
nextLast = last;
last = result;
}
return result;
}Of course, this iterative version is the same as the array The efficiency of the version is also the same.

Related recommendations:
php algorithm learning of dynamic programming
php algorithm learning of Dynamic programming (2)
Detailed explanation of the change problem of dynamic programming
The above is the detailed content of Dynamic programming example analysis of JavaScript advanced algorithms. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1378
1378
 52
52
 How to implement an online speech recognition system using WebSocket and JavaScript
Dec 17, 2023 pm 02:54 PM
How to implement an online speech recognition system using WebSocket and JavaScript
Dec 17, 2023 pm 02:54 PM
How to use WebSocket and JavaScript to implement an online speech recognition system Introduction: With the continuous development of technology, speech recognition technology has become an important part of the field of artificial intelligence. The online speech recognition system based on WebSocket and JavaScript has the characteristics of low latency, real-time and cross-platform, and has become a widely used solution. This article will introduce how to use WebSocket and JavaScript to implement an online speech recognition system.
 WebSocket and JavaScript: key technologies for implementing real-time monitoring systems
Dec 17, 2023 pm 05:30 PM
WebSocket and JavaScript: key technologies for implementing real-time monitoring systems
Dec 17, 2023 pm 05:30 PM
WebSocket and JavaScript: Key technologies for realizing real-time monitoring systems Introduction: With the rapid development of Internet technology, real-time monitoring systems have been widely used in various fields. One of the key technologies to achieve real-time monitoring is the combination of WebSocket and JavaScript. This article will introduce the application of WebSocket and JavaScript in real-time monitoring systems, give code examples, and explain their implementation principles in detail. 1. WebSocket technology
 How to use JavaScript and WebSocket to implement a real-time online ordering system
Dec 17, 2023 pm 12:09 PM
How to use JavaScript and WebSocket to implement a real-time online ordering system
Dec 17, 2023 pm 12:09 PM
Introduction to how to use JavaScript and WebSocket to implement a real-time online ordering system: With the popularity of the Internet and the advancement of technology, more and more restaurants have begun to provide online ordering services. In order to implement a real-time online ordering system, we can use JavaScript and WebSocket technology. WebSocket is a full-duplex communication protocol based on the TCP protocol, which can realize real-time two-way communication between the client and the server. In the real-time online ordering system, when the user selects dishes and places an order
 How to implement an online reservation system using WebSocket and JavaScript
Dec 17, 2023 am 09:39 AM
How to implement an online reservation system using WebSocket and JavaScript
Dec 17, 2023 am 09:39 AM
How to use WebSocket and JavaScript to implement an online reservation system. In today's digital era, more and more businesses and services need to provide online reservation functions. It is crucial to implement an efficient and real-time online reservation system. This article will introduce how to use WebSocket and JavaScript to implement an online reservation system, and provide specific code examples. 1. What is WebSocket? WebSocket is a full-duplex method on a single TCP connection.
 JavaScript and WebSocket: Building an efficient real-time weather forecasting system
Dec 17, 2023 pm 05:13 PM
JavaScript and WebSocket: Building an efficient real-time weather forecasting system
Dec 17, 2023 pm 05:13 PM
JavaScript and WebSocket: Building an efficient real-time weather forecast system Introduction: Today, the accuracy of weather forecasts is of great significance to daily life and decision-making. As technology develops, we can provide more accurate and reliable weather forecasts by obtaining weather data in real time. In this article, we will learn how to use JavaScript and WebSocket technology to build an efficient real-time weather forecast system. This article will demonstrate the implementation process through specific code examples. We
 How to use insertBefore in javascript
Nov 24, 2023 am 11:56 AM
How to use insertBefore in javascript
Nov 24, 2023 am 11:56 AM
Usage: In JavaScript, the insertBefore() method is used to insert a new node in the DOM tree. This method requires two parameters: the new node to be inserted and the reference node (that is, the node where the new node will be inserted).
 Simple JavaScript Tutorial: How to Get HTTP Status Code
Jan 05, 2024 pm 06:08 PM
Simple JavaScript Tutorial: How to Get HTTP Status Code
Jan 05, 2024 pm 06:08 PM
JavaScript tutorial: How to get HTTP status code, specific code examples are required. Preface: In web development, data interaction with the server is often involved. When communicating with the server, we often need to obtain the returned HTTP status code to determine whether the operation is successful, and perform corresponding processing based on different status codes. This article will teach you how to use JavaScript to obtain HTTP status codes and provide some practical code examples. Using XMLHttpRequest
 How to get HTTP status code in JavaScript the easy way
Jan 05, 2024 pm 01:37 PM
How to get HTTP status code in JavaScript the easy way
Jan 05, 2024 pm 01:37 PM
Introduction to the method of obtaining HTTP status code in JavaScript: In front-end development, we often need to deal with the interaction with the back-end interface, and HTTP status code is a very important part of it. Understanding and obtaining HTTP status codes helps us better handle the data returned by the interface. This article will introduce how to use JavaScript to obtain HTTP status codes and provide specific code examples. 1. What is HTTP status code? HTTP status code means that when the browser initiates a request to the server, the service



