Parse 0.1 + 0.2 != 0.3 in js

The number storage in Javascript uses IEEE754 64-bit double-precision floating point number

It is stored as 64-bit in the computer
1 11 52
1: Sign bit 0 Positive number 1 negative number
11: The exponent bit is used to determine the range
52: The mantissa bit is used to determine the precision
Convert to decimal notation:

num = (-1)^s * (1.f) * 2^E
E = e - 1023
s:符号位
e:指数位
f:尾数位
1023偏正值 使得指数位真实取值为[-1023, 1024] 而非 [0, 2047] 目的是为了方便比较大小
实际指数值 = 阶码 - 偏正值
阶码 = 指数的移码 - 1
移码与补码符号为互为取反
举例：
如果指数位实际值为-1
原码：100 0000 0001
反码：111 1111 1110
补码：111 1111 1111
移码：011 1111 1111
阶码：011 1111 1110 = 1022
也可以通过
阶码 = 指数 + 偏正值 = -1 + 1023 = 1022 = 011 1111 1110来计算得到

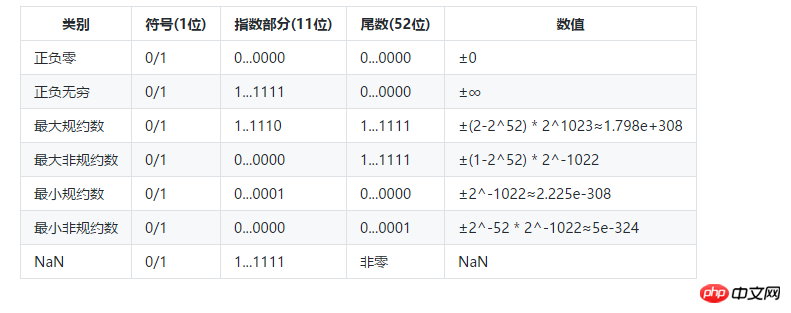
The exponent bit is all 0 and all 1 Special meaning, which will be discussed later, is used to represent +-0 and +-∞

Special values

##Machine precisiondel = 2^-52

Next explain why 0.1 + 0.2 = 0.300000000000000004

First we calculate Binary under 0.1
0.1 * 2 = 0
0.2 * 2 = 0
0.4 * 2 = 0
0.8 * 2 = 1
0.6 * 2 = 1
0.2 * 2 = 0
0.4 * 2 = 0
0.8 * 2 = 1
0.6 * 2 = 1
0.2 * 2 = 0
....
So the binary representation of 0.1 is 0.0001100110011001100 ...loop,
can be converted to 2^-4 * 1.100110011001100...
Since the reserved digits are 52 in total, excluding the leftmost integer bit 1,
so the final value stored in the computer Is: 2^-4 * 1.100 11001100 11001100 11001100 11001100 11001100 11001100 1

Same as 0.2

0.2 * 2 = 0
0.4 * 2 = 0
0.8 * 2 = 1
0.6 * 2 = 1
0.2 * 2 = 0
0.4 * 2 = 0
0.8 * 2 = 1
0.6 * 2 = 1
...
So 0.2 Binary is 0.001100110011001100...loop,
can be converted to 2^-3 * 1.100110011001100...
The easiest value to finally store in the computer is: 2^-3 * 1.100 11001100 11001100 11001100 11001100 110 01100 11001100 1
Add the two
0.0001100 11001100 11001100 11001100 11001100 11001100 11001100 1
+
0.001100 11001100 11001100 11001100 110011 00 11001100 11001100 1
= 0.0 10011001 10011001 10011001 10011001 10011001 10011001 10011
≈ 0.30000000000000004

The above is the detailed content of Parse 0.1 + 0.2 != 0.3 in js. For more information, please follow other related articles on the PHP Chinese website!