How raphael.js implements angle to radian conversion
This article mainly shares with you how raphael.js realizes the conversion of angles and radians. It has a good reference value and I hope it will be helpful to everyone. Let’s follow the editor and take a look.
The relationship between radians and angles
1. Two units of angles
“ Radians ” and “degree” are two different units for measuring angle size. Just like "meter" and "meter" are two different units of measuring length.
It is stipulated in flash that the angle in the rotation angle (rotation) is in "degrees" as the unit; and the angle in the trigonometric function must be in "radians" as the unit. This rule is the first thing we need to remember! ! ! For example: rotation2 - is a rotation of "2 degrees"; sin (π/2) - is the sine of an angle with a size of "π/2 radians".
2. The definition of radian
The so-called "definition of radian" means, how is the angle size of 1 radian defined?
We know that the definition of "degree" is, "Two rays are emitted from the center of the circle to the circumference, forming an included angle and an arc directly opposite the included angle. When the length of this arc is exactly equal to one-360th of the circumference of the circle, The angle between the two rays is 1 degree. (Figure 1)
So, how is the radian defined? The definition of radian is: two rays shoot from the center to the circumference, forming an included angle and an included angle. When the length of this arc is exactly equal to the radius of the circle, the angle between the two rays is 1 radian. (Figure 2)
Compare these two definitions of degrees and radians. Similar. The only difference between them is that the length of the arc subtended by the angle is different. The degree is equal to one-third of the circumference of the circle, while the radian is equal to the radius. Simply put, the definition of radian is that when the angle is When the length of the arc subtended by the angle is equal to the radius, the size of the angle is 1 radian.
Related pictures for this topic are as follows:
## If the length of the arc subtended by the angle is several times the radius, then the size of the angle Just a few radians. 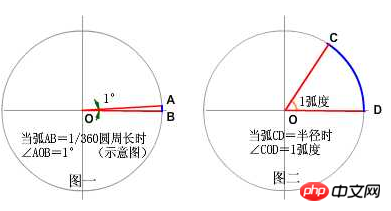 Their relationship can be expressed and calculated by the following formula:
Their relationship can be expressed and calculated by the following formula:
Angle (radians) = arc length/radius
The circumference of a circle is 2π times the radius, so a circumferential angle (360 degrees) is 2π radians.
The length of a semicircle is π times the radius, so a straight angle (180 degrees) is π radians
3. Conversion between degrees and radians
According to the above, a straight angle is π radians. π radians.
That is, 180 degrees = π radians
It can be seen that:
1 degree = π/180 radians (≈0.017453 radians)
Therefore, the formula for converting degrees into radians is obtained:
Radians = Degrees 45×π/180 =π/4 radians
30°=30×π/180 =π/6 radians
120°=120×π/180 =2π/3 radians
In turn, radians become How to calculate degrees?
Because π radians = 180°
So 1 radians = 180°/π (≈57.3°)
Therefore, the formula for converting radians into degrees can be obtained:
Degrees = radians × 180°/π
For example:
4π/3 radians = 4π/3 ×180°/π
= 240°
Maybe some friends will say that it is multiplied by "π/180". Or "180°/π" is easy to get wrong. In fact, you just need to remember: π is π radians, and 180 is 180 degrees. Which unit I want to convert into, I have to put it on the numerator. To convert to radians, place π radians on the numerator - multiply by π/180. In addition, 1 degree is much smaller than 1 radian, only about 0.017453 radians (π/180≈0.017453). Therefore, after converting degrees into radians, the number must become smaller, so when converting into radians, it must be multiplied by π/180. If you can think about it this way, you won't make a mistake.
Write "π" as "PI" in the AS code. And because "π" and "sin" are both "mathematical functions", according to regulations, "Math." must be added in front (Math is the abbreviation of "Mathematics" in English), and then written as "Math.PI", "Math.sin".
So sin30° must be written as Math.sin (30*Math.PI/180). The part in parentheses is to convert 30° into radians, that is, 30×π/180.
/*\
* Raphael.rad
[ method ]
**
* Transform angle to radians
> Parameters
- deg (number) angle in degrees
= (number) angle in radians.
\*/
R.rad = function (deg) { //角度degrees转化成弧度radians
return deg % 360 * PI / 180;
};
/*\
* Raphael.deg
[ method ]
**
* Transform angle to degrees
> Parameters
- rad (number) angle in radians
= (number) angle in degrees.
\*/
R.deg = function (rad) { //弧度radians转化成角度degrees
return Math.round ((rad * 180 / PI% 360)* 1000) / 1000;
};Related recommendations:
Conversion of radians and angles
Understand the concepts and conversion relationships of angles and radians
The above is the detailed content of How raphael.js implements angle to radian conversion. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1385
1385
 52
52
 A simple guide to converting USDT ERC20 to TRC20
Jan 18, 2024 pm 06:09 PM
A simple guide to converting USDT ERC20 to TRC20
Jan 18, 2024 pm 06:09 PM
We teach you step by step how to convert USDTERC20 to TRC20 network. This is because many people like to move the USDT stablecoin from the Ethereum network to the Tron network to save on transaction fees. So, if you want to convert your ERC-20 tokens to TRC-20, I believe this tutorial will be helpful to you. The difference between ERC-20 and TRC-20 ERC-20 tokens and TRC-20 tokens represent tokens based on the Ethereum network and the Tron network respectively. There are some differences between the two networks, mainly in the following aspects: First, the Ethereum network often faces congestion and high gas fees, which may lead to transaction delays and high transaction costs. In comparison, the Tron network is relatively less congested
 Practical tips for converting full-width English letters into half-width form
Mar 26, 2024 am 09:54 AM
Practical tips for converting full-width English letters into half-width form
Mar 26, 2024 am 09:54 AM
Practical tips for converting full-width English letters into half-width forms. In modern life, we often come into contact with English letters, and we often need to input English letters when using computers, mobile phones and other devices. However, sometimes we encounter full-width English letters, and we need to use the half-width form. So, how to convert full-width English letters to half-width form? Here are some practical tips for you. First of all, full-width English letters and numbers refer to characters that occupy a full-width position in the input method, while half-width English letters and numbers occupy a full-width position.
 How to convert AI files to CDR format
Feb 19, 2024 pm 04:09 PM
How to convert AI files to CDR format
Feb 19, 2024 pm 04:09 PM
AI files refer to vector graphics files created by Adobe Illustrator (AI for short) software, while CDR files refer to vector graphics files created by CorelDRAW software. Since these two softwares are developed by different manufacturers, their file formats are different and cannot be directly converted to each other. However, we can convert AI files to CDR files through some methods. A commonly used conversion method will be introduced below. Step 1: Export AI files to EPS format AdobeIllust
 How to convert ODT to Word in Windows 11/10?
Feb 20, 2024 pm 12:21 PM
How to convert ODT to Word in Windows 11/10?
Feb 20, 2024 pm 12:21 PM
In this article, we will show you how to convert OpenDocumentTextDocument (ODT) files to Microsoft Word (Docx, DOC, etc.). Format. How to Convert ODT to Word in Windows 11/10 Here is how you can convert ODT documents to DOC or DOCX format on Windows PC: Convert ODT to Word using WordPad or Word The first method we are going to show you Is to use WordPad or MicrosoftWord to convert ODT to Word. Here are the steps to achieve this: First, open the WordPad app using the Start menu. Now, go to
 How to convert a virtual machine to a physical machine?
Feb 19, 2024 am 11:40 AM
How to convert a virtual machine to a physical machine?
Feb 19, 2024 am 11:40 AM
Converting a virtual machine (VM) to a physical machine is the process of migrating a virtual instance and associated application software to a physical hardware platform. This conversion helps optimize operating system performance and hardware resource utilization. This article aims to provide an in-depth look at how to make this conversion. How to implement migration from virtual machine to physical machine? Typically, the conversion process between a virtual machine and a physical machine is performed outside the virtual machine by third-party software. This process consists of multiple stages involving the configuration of virtual machines and the transfer of resources. Prepare the physical machine: The first step is to ensure that the physical machine meets the hardware requirements for Windows. We need to back up the data on a physical machine as the conversion process will overwrite the existing data. *Username and password for an administrator account with administrator rights to create system images. will be virtual
 Golang time processing: How to convert timestamp to string in Golang
Feb 24, 2024 pm 10:42 PM
Golang time processing: How to convert timestamp to string in Golang
Feb 24, 2024 pm 10:42 PM
Golang time conversion: How to convert timestamp to string In Golang, time operation is one of the very common operations. Sometimes we need to convert the timestamp into a string for easy display or storage. This article will introduce how to use Golang to convert timestamps to strings and provide specific code examples. 1. Conversion of timestamps and strings In Golang, timestamps are usually expressed in the form of integer numbers, which represent the number of seconds from January 1, 1970 to the current time. The string is
 Detailed explanation of the implementation method of converting PHP months to English months
Mar 21, 2024 pm 06:45 PM
Detailed explanation of the implementation method of converting PHP months to English months
Mar 21, 2024 pm 06:45 PM
This article will introduce in detail how to convert months in PHP to English months, and give specific code examples. In PHP development, sometimes we need to convert digital months to English months, which is very practical in some date processing or data display scenarios. The implementation principles, specific code examples and precautions will be explained in detail below. 1. Implementation principle In PHP, you can convert digital months into English months by using the DateTime class and format method. Date
 How to convert qq music to mp3 format Convert qq music to mp3 format on mobile phone
Mar 21, 2024 pm 01:21 PM
How to convert qq music to mp3 format Convert qq music to mp3 format on mobile phone
Mar 21, 2024 pm 01:21 PM
QQ Music allows everyone to enjoy watching movies and relieve boredom. You can use this software every day to easily satisfy your needs. A large number of high-quality songs are available for everyone to listen to. You can also download and save them. The next time you listen to them, you don’t need an Internet connection. The songs downloaded here are not in MP3 format and cannot be used on other platforms. After the membership songs expire, there is no way to listen to them again. Therefore, many friends want to convert the songs into MP3 format. Here, the editor explains You provide methods so that everyone can use them! 1. Open QQ Music on your computer, click the [Main Menu] button in the upper right corner, click [Audio Transcoding], select the [Add Song] option, and add the songs that need to be converted; 2. After adding the songs, click to select Convert to [mp3]




