
This article mainly shares with you how to distinguish linearity in Python programming. Friends who need it can take a look.
"""
Author: Victoria
Created on: 2017.9.15 11:45
"""
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
def LDA(X0, X1):
"""
Get the optimal params of LDA model given training data.
Input:
X0: np.array with shape [N1, d]
X1: np.array with shape [N2, d]
Return:
omega: np.array with shape [1, d]. Optimal params of LDA.
"""
#shape [1, d]
mean0 = np.mean(X0, axis=0, keepdims=True)
mean1 = np.mean(X1, axis=0, keepdims=True)
Sw = (X0-mean0).T.dot(X0-mean0) + (X1-mean1).T.dot(X1-mean1)
omega = np.linalg.inv(Sw).dot((mean0-mean1).T)
return omega
if __name__=="__main__":
#read data from xls
work_book = pd.read_csv("../data/watermelon_3a.csv", header=None)
positive_data = work_book.values[work_book.values[:, -1] == 1.0, :]
negative_data = work_book.values[work_book.values[:, -1] == 0.0, :]
print (positive_data)
#LDA
omega = LDA(negative_data[:, 1:-1], positive_data[:, 1:-1])
#plot
plt.plot(positive_data[:, 1], positive_data[:, 2], "bo")
plt.plot(negative_data[:, 1], negative_data[:, 2], "r+")
lda_left = 0
lda_right = -(omega[0]*0.9) / omega[1]
plt.plot([0, 0.9], [lda_left, lda_right], 'g-')
plt.xlabel('density')
plt.ylabel('sugar rate')
plt.title("LDA")
plt.show()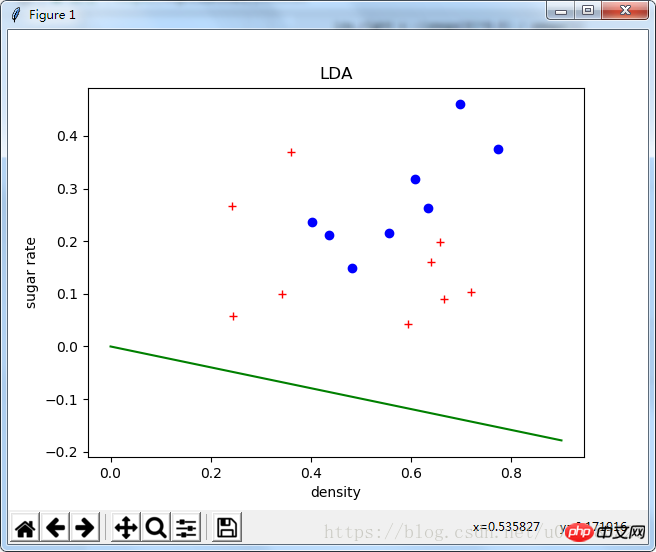
Related recommendations:
A concise introductory tutorial on linear discriminant analysis
The above is the detailed content of How to identify linearity in Python programming. For more information, please follow other related articles on the PHP Chinese website!




