
This article mainly introduces Python's method of solving the greatest common divisor based on the euclidean division method. It analyzes the implementation method and optimization operation skills of Python using the euclidean division method to solve the greatest common divisor in the form of examples. Friends in need can refer to the following
The example in this article describes Python's method of solving the greatest common divisor based on the euclidean division method. Share it with everyone for your reference, the details are as follows:
I have summarized the solution of the greatest common divisor in Knuth TAOCP before. In fact, the algorithm modification in the after-school questions requires the realization of the solution of the greatest common divisor by euclidean division. .
My initial understanding of this question was wrong, and naturally I didn’t have a standard answer. Now write the corresponding code implementation according to the standard answer:
# -*- coding:utf-8 -*-
#! python2
def MaxCommpisor(m,n):
while m * n != 0:
m = m % n
if m == 0:
return n
else:
n = n % m
if n == 0:
return m
print(MaxCommpisor(55,120))The execution result of the program:
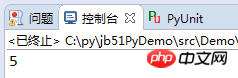
Exchange the positions of the two numbers. The code is as follows:
# -*- coding:utf-8 -*-
#! python2
def MaxCommpisor(m,n):
while m * n != 0:
m = m % n
if m == 0:
return n
else:
n = n % m
if n == 0:
return m
print(MaxCommpisor(120,55))The execution result of the program:

def CommDevisor(m,n):
r = m % n
while r != 0:
m = n
n = r
r = m % n
return n
print(CommDevisor(120,25))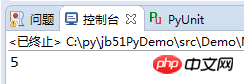
PS: Here are several calculation tools recommended for your further reference:
Online one-variable function (Equation) solving calculation tools:
http://tools.jb51.net/jisuanqi/equ_jisuanqi
Scientific calculator online use_advanced calculator Online calculation:
http://tools.jb51.net/jisuanqi/jsqkexue
Online Calculator_Standard Calculator:
http://tools.jb51.net/jisuanqi/jsq
php Summary of common algorithms for calculating the greatest common divisor of two integers_PHP tutorial
How to use Python to solve the greatest common divisor
##
The above is the detailed content of Python example of how to find the greatest common divisor based on euclidean division. For more information, please follow other related articles on the PHP Chinese website!




