Backend Development
Backend Development
 Python Tutorial
Python Tutorial
 Python tests whether Jarque-Bera conforms to normal distribution
Python tests whether Jarque-Bera conforms to normal distribution
Python tests whether Jarque-Bera conforms to normal distribution
The content of this article is to test whether Jarque-Bera conforms to the normal distribution in python. It has a certain reference value. Friends in need can refer to it
Normal distribution is a normality test of a population distribution. When the sequence obeys the normal distribution, the JB statistic:
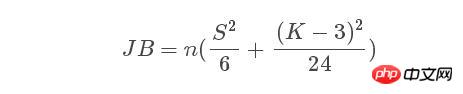
##gradually obeys distributed. Where n is the sample size, S and K are the skewness and kurtosis of the random variable respectively. Calculated as follows:
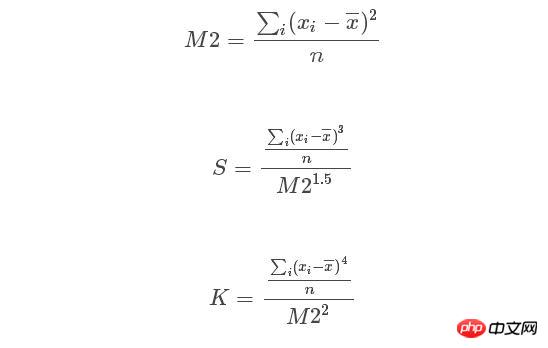
#The functions called for skewness and kurtosis in python's sicipy.stats are
stats.skew(y)
, stats.kurtosis(y), where the formula of kurtosis is In excel, the calculation formulas for skewness and kurtosis are as follows :
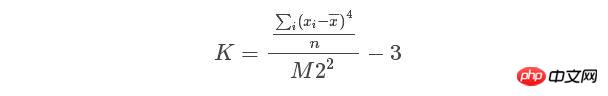
Code
# Next, implement the formulas for calculating skewness and skew in Python's scipy library and establish a normal distribution test.Resultimport numpy as npimport scipy.stats as statsdef self_JBtest(y): # 样本规模n n = y.size y_ = y - y.mean() """ M2:二阶中心钜 skew 偏度 = 三阶中心矩 与 M2^1.5的比 krut 峰值 = 四阶中心钜 与 M2^2 的比 """ M2 = np.mean(y_**2) skew = np.mean(y_**3)/M2**1.5 krut = np.mean(y_**4)/M2**2 """ 计算JB统计量,以及建立假设检验 """ JB = n*(skew**2/6 + (krut-3 )**2/24) pvalue = 1 - stats.chi2.cdf(JB,df=2) print("偏度:",stats.skew(y),skew) print("峰值:",stats.kurtosis(y)+3,krut) print("JB检验:",stats.jarque_bera(y)) return np.array([JB,pvalue]) y1 = stats.norm.rvs(size=10) y2 = stats.t.rvs(size=1000,df=4) print(self_JBtest(y1)) print(self_JBtest(y2))Copy after login=============== RESTART: C:\Users\tinysoft\Desktop\JB正态性检验.py =============== 偏度: 0.5383125387398069 0.53831253874 峰值: 2.9948926317585918 2.99489263176 JB检验: (0.48297818444514068, 0.78545737133644544) [ 0.48297818 0.78545737] 偏度: -1.0488825341925703 -1.04888253419 峰值: 13.40804986639119 13.4080498664 JB检验: (4697.0050126426095, 0.0) [ 4697.00501264 0. ]Copy after login
The above is the detailed content of Python tests whether Jarque-Bera conforms to normal distribution. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1386
1386
 52
52
 How to run programs in terminal vscode
Apr 15, 2025 pm 06:42 PM
How to run programs in terminal vscode
Apr 15, 2025 pm 06:42 PM
In VS Code, you can run the program in the terminal through the following steps: Prepare the code and open the integrated terminal to ensure that the code directory is consistent with the terminal working directory. Select the run command according to the programming language (such as Python's python your_file_name.py) to check whether it runs successfully and resolve errors. Use the debugger to improve debugging efficiency.
 Can visual studio code be used in python
Apr 15, 2025 pm 08:18 PM
Can visual studio code be used in python
Apr 15, 2025 pm 08:18 PM
VS Code can be used to write Python and provides many features that make it an ideal tool for developing Python applications. It allows users to: install Python extensions to get functions such as code completion, syntax highlighting, and debugging. Use the debugger to track code step by step, find and fix errors. Integrate Git for version control. Use code formatting tools to maintain code consistency. Use the Linting tool to spot potential problems ahead of time.
 Is the vscode extension malicious?
Apr 15, 2025 pm 07:57 PM
Is the vscode extension malicious?
Apr 15, 2025 pm 07:57 PM
VS Code extensions pose malicious risks, such as hiding malicious code, exploiting vulnerabilities, and masturbating as legitimate extensions. Methods to identify malicious extensions include: checking publishers, reading comments, checking code, and installing with caution. Security measures also include: security awareness, good habits, regular updates and antivirus software.
 Can vs code run in Windows 8
Apr 15, 2025 pm 07:24 PM
Can vs code run in Windows 8
Apr 15, 2025 pm 07:24 PM
VS Code can run on Windows 8, but the experience may not be great. First make sure the system has been updated to the latest patch, then download the VS Code installation package that matches the system architecture and install it as prompted. After installation, be aware that some extensions may be incompatible with Windows 8 and need to look for alternative extensions or use newer Windows systems in a virtual machine. Install the necessary extensions to check whether they work properly. Although VS Code is feasible on Windows 8, it is recommended to upgrade to a newer Windows system for a better development experience and security.
 Python: Automation, Scripting, and Task Management
Apr 16, 2025 am 12:14 AM
Python: Automation, Scripting, and Task Management
Apr 16, 2025 am 12:14 AM
Python excels in automation, scripting, and task management. 1) Automation: File backup is realized through standard libraries such as os and shutil. 2) Script writing: Use the psutil library to monitor system resources. 3) Task management: Use the schedule library to schedule tasks. Python's ease of use and rich library support makes it the preferred tool in these areas.
 What is vscode What is vscode for?
Apr 15, 2025 pm 06:45 PM
What is vscode What is vscode for?
Apr 15, 2025 pm 06:45 PM
VS Code is the full name Visual Studio Code, which is a free and open source cross-platform code editor and development environment developed by Microsoft. It supports a wide range of programming languages and provides syntax highlighting, code automatic completion, code snippets and smart prompts to improve development efficiency. Through a rich extension ecosystem, users can add extensions to specific needs and languages, such as debuggers, code formatting tools, and Git integrations. VS Code also includes an intuitive debugger that helps quickly find and resolve bugs in your code.
 Can visual studio code run python
Apr 15, 2025 pm 08:00 PM
Can visual studio code run python
Apr 15, 2025 pm 08:00 PM
VS Code not only can run Python, but also provides powerful functions, including: automatically identifying Python files after installing Python extensions, providing functions such as code completion, syntax highlighting, and debugging. Relying on the installed Python environment, extensions act as bridge connection editing and Python environment. The debugging functions include setting breakpoints, step-by-step debugging, viewing variable values, and improving debugging efficiency. The integrated terminal supports running complex commands such as unit testing and package management. Supports extended configuration and enhances features such as code formatting, analysis and version control.
 Can vs code run python
Apr 15, 2025 pm 08:21 PM
Can vs code run python
Apr 15, 2025 pm 08:21 PM
Yes, VS Code can run Python code. To run Python efficiently in VS Code, complete the following steps: Install the Python interpreter and configure environment variables. Install the Python extension in VS Code. Run Python code in VS Code's terminal via the command line. Use VS Code's debugging capabilities and code formatting to improve development efficiency. Adopt good programming habits and use performance analysis tools to optimize code performance.