
This article mainly introduces the implementation of heap sorting in JS, which has certain reference value. Now I share it with everyone. Friends in need can refer to
The heap is a complete binary tree.
Complete binary tree: Except for the last layer of the binary tree, the number of nodes in other layers reaches the maximum, and all the nodes in the last layer are concentrated on the left (when the nodes on the left are full, Nodes can be missing only on the right).
Big top heap: The root node is the maximum value, and the value of each node is greater than or equal to the value of its child node.
Small top heap: The root node is the minimum value, and the value of each node is less than or equal to the value of its child node.
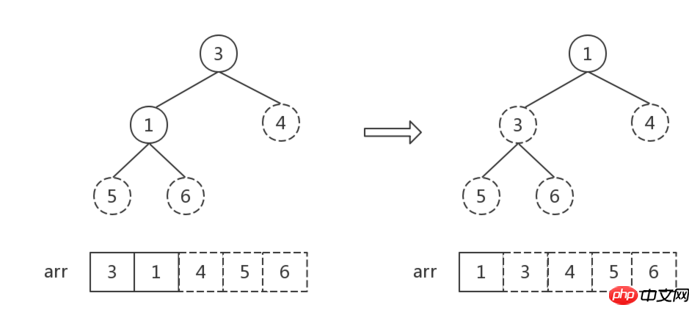
Heap storage: The heap is implemented by an array, which is equivalent to a level-order traversal of a binary tree. As shown below:


i 1 and 2i 2 .
Heap sort algorithm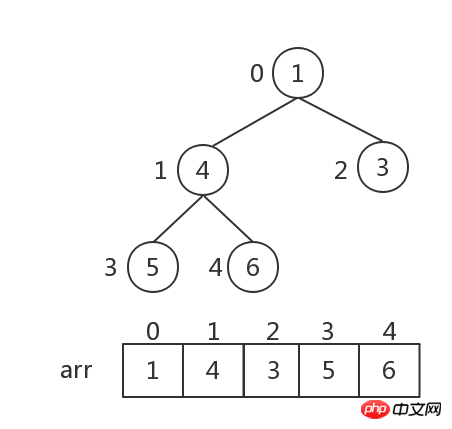
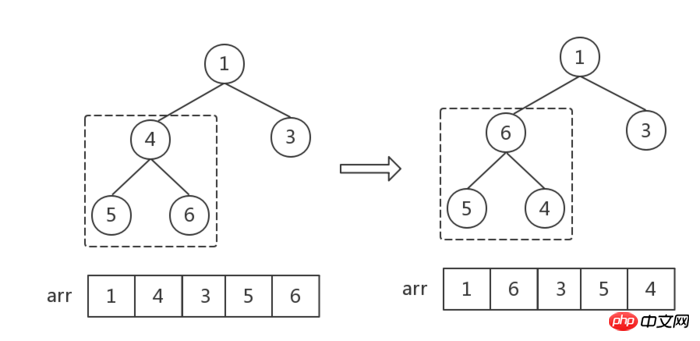
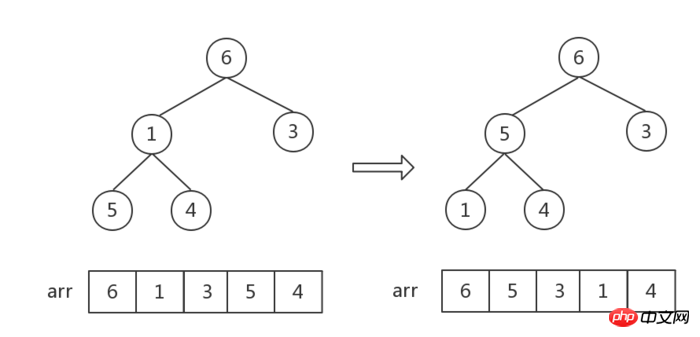
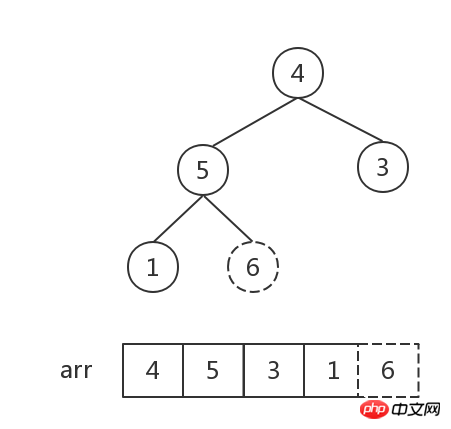
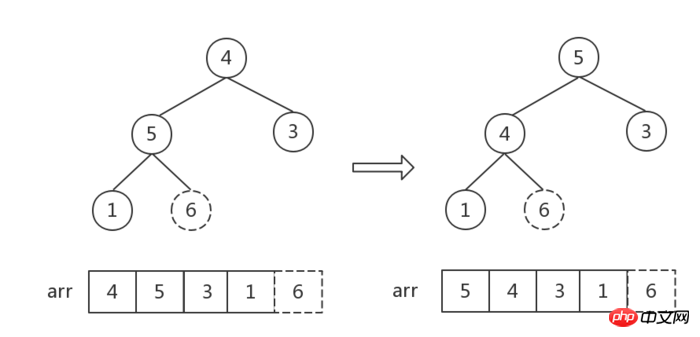
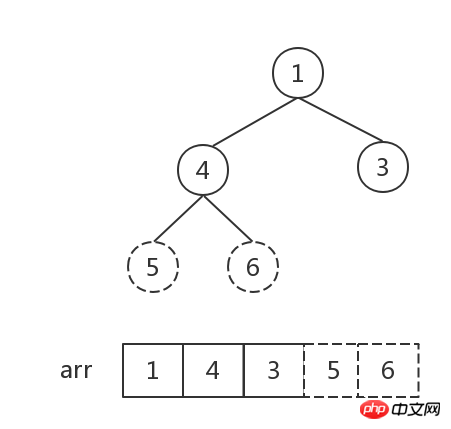
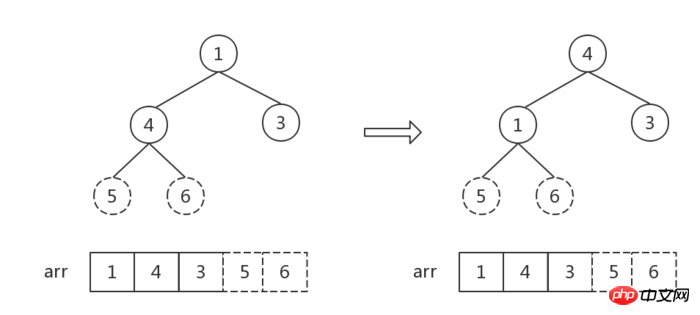
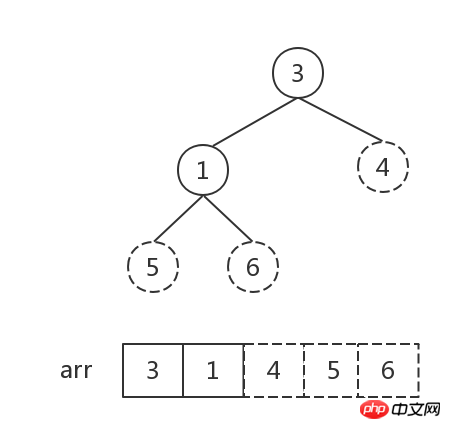
 ##The number of elements in the heap is 1, sort Finish.
##The number of elements in the heap is 1, sort Finish.
// 交换两个节点
function swap(A, i, j) {
let temp = A[i];
A[i] = A[j];
A[j] = temp;
}
// 将 i 结点以下的堆整理为大顶堆,注意这一步实现的基础实际上是:
// 假设 结点 i 以下的子堆已经是一个大顶堆,adjustheap 函数实现的
// 功能是实际上是:找到 结点 i 在包括结点 i 的堆中的正确位置。后面
// 将写一个 for 循环,从第一个非叶子结点开始,对每一个非叶子结点
// 都执行 adjustheap 操作,所以就满足了结点 i 以下的子堆已经是一大
//顶堆
function adjustHeap(A, i, length) {
let temp = A[i]; // 当前父节点
// j<length function>=0; i--) {
adjustHeap(A, i, A.length);
}
// 排序,每一次for循环找出一个当前最大值,数组长度减一
for(let i = Math.floor(A.length-1); i>0; i--) {
swap(A, 0, i); // 根节点与最后一个节点交换
adjustHeap(A, 0, i); // 从根节点开始调整,并且最后一个结点已经为当
// 前最大值,不需要再参与比较,所以第三个参数
// 为 i,即比较到最后一个结点前一个即可
}
}
let Arr = [4, 6, 8, 5, 9, 1, 2, 5, 3, 2];
heapSort(Arr);
alert(Arr);</length>Program notes: Arrange the heap below node i into a large top heap. Note that the basis for this step is actually: assuming that the sub-heap below node i is already a large top heap. On the top heap, the function implemented by the adjustHeap function is actually to find the correct position of node i in the heap including node i. When doing the first heap later, a for loop is written in heapSort. Starting from the first non-leaf node, the adjustHeap operation is performed on each non-leaf node, so it is satisfied that in each adjustHeap, the node The sub-heap below i is already a large top-heap.
Complexity analysis: The adjustHeap function only traverses one node per layer of the heap, because
The depth of a complete binary tree with n nodes is [log2n] 1, so the complexity of adjustHeap The degree is O(logn), and the outer loop has f(n) times, so the final complexity is O(nlogn).
Heap is mainly used to implement priority queue. The following is an application example of priority queue:
The operating system dynamically selects priority Supreme mission execution.
In a static problem, to select the top M names among N elements, the complexity of using sorting is: O(NlogN), and the complexity of using priority queue is: O(NlogM).
The different complexities of implementing priority queues using ordinary arrays, sequential arrays and heaps are as follows:
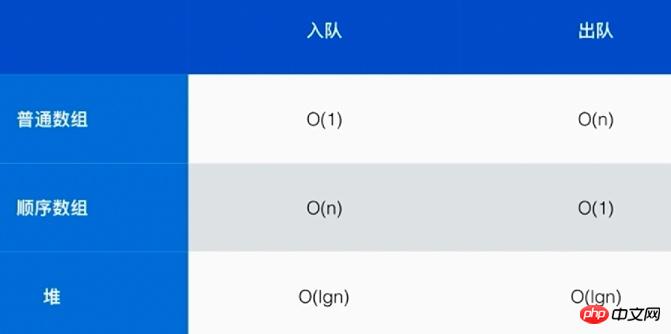
Use heaps to implement priority Queues can make the complexity of joining and dequeuing very low.
The above is the entire content of this article. I hope it will be helpful to everyone's study. For more related content, please pay attention to the PHP Chinese website!
Related recommendations:
The above is the detailed content of JS implements heap sorting. For more information, please follow other related articles on the PHP Chinese website!




