 Backend Development
Backend Development
 Python Tutorial
Python Tutorial
 Introduction to knowledge about the complexity of sequential list algorithms in Python
Introduction to knowledge about the complexity of sequential list algorithms in Python
Introduction to knowledge about the complexity of sequential list algorithms in Python
This article brings you knowledge about the complexity of sequential table algorithms in Python. It has certain reference value. Friends in need can refer to it. I hope it will be helpful to you.
1. Introduction of algorithm complexity
For the time and space properties of the algorithm, the most important thing is its magnitude and trend, so the function to measure its complexity The constant factor can be ignored.
Big O notation is usually the asymptotic time complexity of a certain algorithm. The complexity of commonly used asymptotic complexity functions is compared as follows:
O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)
Introducing examples of time complexity, please compare the two code examples to see the calculation results
import time
start_time = time.time()
for a in range(0,1001):
for b in range(0,1001):
for c in range(0,1001):
if a+b+c ==1000 and a**2 + b**2 == c**2:
print("a, b, c :%d, %d, %d" % (a, b ,c))
end_time = time.time()
print("times:%d" % (end_time-start_time))
print("完成")

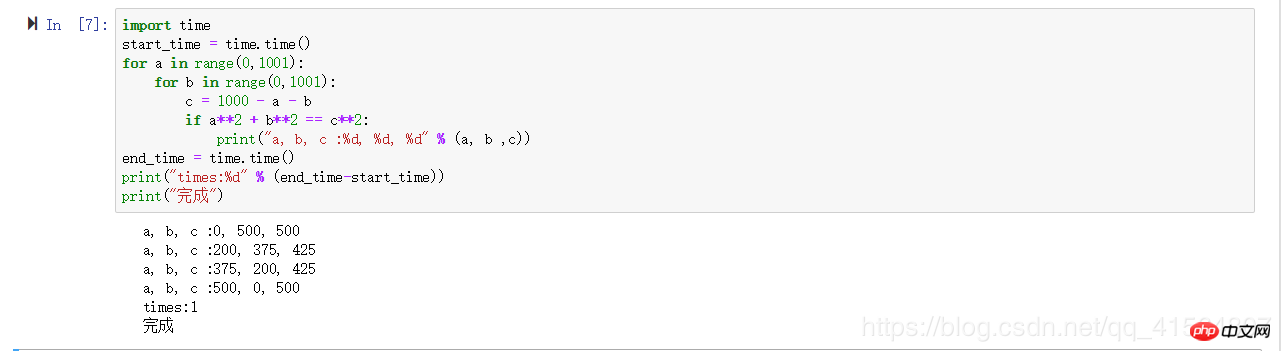
import time
start_time = time.time()
for a in range(0,1001):
for b in range(0,1001):
c = 1000 - a - b
if a**2 + b**2 == c**2:
print("a, b, c :%d, %d, %d" % (a, b ,c))
end_time = time.time()
print("times:%d" % (end_time-start_time))
print("完成")
How to calculate time complexity:
# 时间复杂度计算 # 1.基本步骤,基本操作,复杂度是O(1) # 2.顺序结构,按加法计算 # 3.循环,按照乘法 # 4.分支结构采用其中最大值 # 5.计算复杂度,只看最高次项,例如n^2+2的复杂度是O(n^2)
2. Time complexity of sequence list
Test of time complexity of list
# 测试
from timeit import Timer
def test1():
list1 = []
for i in range(10000):
list1.append(i)
def test2():
list2 = []
for i in range(10000):
# list2 += [i] # +=本身有优化,所以不完全等于list = list + [i]
list2 = list2 + [i]
def test3():
list3 = [i for i in range(10000)]
def test4():
list4 = list(range(10000))
def test5():
list5 = []
for i in range(10000):
list5.extend([i])
timer1 = Timer("test1()","from __main__ import test1")
print("append:",timer1.timeit(1000))
timer2 = Timer("test2()","from __main__ import test2")
print("+:",timer2.timeit(1000))
timer3 = Timer("test3()","from __main__ import test3")
print("[i for i in range]:",timer3.timeit(1000))
timer4 = Timer("test4()","from __main__ import test4")
print("list(range):",timer4.timeit(1000))
timer5 = Timer("test5()","from __main__ import test5")
print("extend:",timer5.timeit(1000))
Output result

Complexity of methods in the list:
# 列表方法中复杂度 # index O(1) # append 0(1) # pop O(1) 无参数表示是从尾部向外取数 # pop(i) O(n) 从指定位置取,也就是考虑其最复杂的状况是从头开始取,n为列表的长度 # del O(n) 是一个个删除 # iteration O(n) # contain O(n) 其实就是in,也就是说需要遍历一遍 # get slice[x:y] O(K) 取切片,即K为Y-X # del slice O(n) 删除切片 # set slice O(n) 设置切片 # reverse O(n) 逆置 # concatenate O(k) 将两个列表加到一起,K为第二个列表的长度 # sort O(nlogn) 排序,和排序算法有关 # multiply O(nk) K为列表的长度
Complexity of methods in dictionary (supplementary)
# 字典中的复杂度 # copy O(n) # get item O(1) # set item O(1) 设置 # delete item O(1) # contains(in) O(1) 字典不用遍历,所以可以一次找到 # iteration O(n)
3. Data structure of sequence table
The complete information of a sequence table includes two parts, one part is the set of elements in the table, and the other part is to achieve correct operation The information that needs to be recorded mainly includes the capacity of the element storage area and the number of elements in the current table.
#Combination of header and data area: integrated structure: header information (recording capacity and number of existing elements) and data area for continuous storage
Separate structure: header information and data area are not stored continuously, and some information will be used to store address units to point to the real data area
The differences and advantages and disadvantages between the two:
# 1.一体式结构:数据必须整体迁移 # 2.分离式结构:在数据动态的过错中有优势
# 申请多大的空间? # 扩充政策: # 1.每次增加相同的空间,线性增长 # 特点:节省空间但操作次数多 # 2.每次扩容加倍,例如每次扩充增加一倍 # 特点:减少执行次数,用空间换效率 # 数据表的操作: # 1.增加元素: # a.尾端加入元素,时间复杂度为O(1) # b.非保序的元素插入:O(1) # c.保序的元素插入:时间度杂度O(n)(保序不改变其原有的顺序) # 2.删除元素: # a.末尾:时间复杂度:O(1) # b.非保序:O(1) # c.保序:O(n) # python中list与tuple采用了顺序表的实现技术 # list可以按照下标索引,时间度杂度O(1),采用的是分离式的存储区,动态顺序表
4. Strategies for variable space expansion in python
1. When creating an empty table (or a very small table), the system allocates a storage area that can accommodate 8 elements
2. When performing insert operations (insert, append), if the element storage area is full, replace it with a storage area of 4 Double the storage area
3. If the table is already very large (the threshold is 50000), change the policy and adopt the method of doubling the size. To avoid too much free space.
The above is the detailed content of Introduction to knowledge about the complexity of sequential list algorithms in Python. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1387
1387
 52
52
 Is the vscode extension malicious?
Apr 15, 2025 pm 07:57 PM
Is the vscode extension malicious?
Apr 15, 2025 pm 07:57 PM
VS Code extensions pose malicious risks, such as hiding malicious code, exploiting vulnerabilities, and masturbating as legitimate extensions. Methods to identify malicious extensions include: checking publishers, reading comments, checking code, and installing with caution. Security measures also include: security awareness, good habits, regular updates and antivirus software.
 How to run programs in terminal vscode
Apr 15, 2025 pm 06:42 PM
How to run programs in terminal vscode
Apr 15, 2025 pm 06:42 PM
In VS Code, you can run the program in the terminal through the following steps: Prepare the code and open the integrated terminal to ensure that the code directory is consistent with the terminal working directory. Select the run command according to the programming language (such as Python's python your_file_name.py) to check whether it runs successfully and resolve errors. Use the debugger to improve debugging efficiency.
 Can vs code run in Windows 8
Apr 15, 2025 pm 07:24 PM
Can vs code run in Windows 8
Apr 15, 2025 pm 07:24 PM
VS Code can run on Windows 8, but the experience may not be great. First make sure the system has been updated to the latest patch, then download the VS Code installation package that matches the system architecture and install it as prompted. After installation, be aware that some extensions may be incompatible with Windows 8 and need to look for alternative extensions or use newer Windows systems in a virtual machine. Install the necessary extensions to check whether they work properly. Although VS Code is feasible on Windows 8, it is recommended to upgrade to a newer Windows system for a better development experience and security.
 Can visual studio code be used in python
Apr 15, 2025 pm 08:18 PM
Can visual studio code be used in python
Apr 15, 2025 pm 08:18 PM
VS Code can be used to write Python and provides many features that make it an ideal tool for developing Python applications. It allows users to: install Python extensions to get functions such as code completion, syntax highlighting, and debugging. Use the debugger to track code step by step, find and fix errors. Integrate Git for version control. Use code formatting tools to maintain code consistency. Use the Linting tool to spot potential problems ahead of time.
 Choosing Between PHP and Python: A Guide
Apr 18, 2025 am 12:24 AM
Choosing Between PHP and Python: A Guide
Apr 18, 2025 am 12:24 AM
PHP is suitable for web development and rapid prototyping, and Python is suitable for data science and machine learning. 1.PHP is used for dynamic web development, with simple syntax and suitable for rapid development. 2. Python has concise syntax, is suitable for multiple fields, and has a strong library ecosystem.
 Can vscode be used for mac
Apr 15, 2025 pm 07:36 PM
Can vscode be used for mac
Apr 15, 2025 pm 07:36 PM
VS Code is available on Mac. It has powerful extensions, Git integration, terminal and debugger, and also offers a wealth of setup options. However, for particularly large projects or highly professional development, VS Code may have performance or functional limitations.
 PHP and Python: Different Paradigms Explained
Apr 18, 2025 am 12:26 AM
PHP and Python: Different Paradigms Explained
Apr 18, 2025 am 12:26 AM
PHP is mainly procedural programming, but also supports object-oriented programming (OOP); Python supports a variety of paradigms, including OOP, functional and procedural programming. PHP is suitable for web development, and Python is suitable for a variety of applications such as data analysis and machine learning.
 Can vscode run ipynb
Apr 15, 2025 pm 07:30 PM
Can vscode run ipynb
Apr 15, 2025 pm 07:30 PM
The key to running Jupyter Notebook in VS Code is to ensure that the Python environment is properly configured, understand that the code execution order is consistent with the cell order, and be aware of large files or external libraries that may affect performance. The code completion and debugging functions provided by VS Code can greatly improve coding efficiency and reduce errors.



