Representation range of floating point numbers-JS Tutorial-php.cn

Floating point numbers are composed of three parts: symbol, exponent and mantissa. Floating point numbers are divided into single precision floating point numbers and double precision floating point numbers. The range of single precision floating point numbers is -3.4E38 ~3.4E38, the range of double-precision floating point numbers is -1.79E 308 ~ 1.79E 308

Representation range of floating point numbers

[Recommended course: JavaScript Tutorial]

Floating point number representation

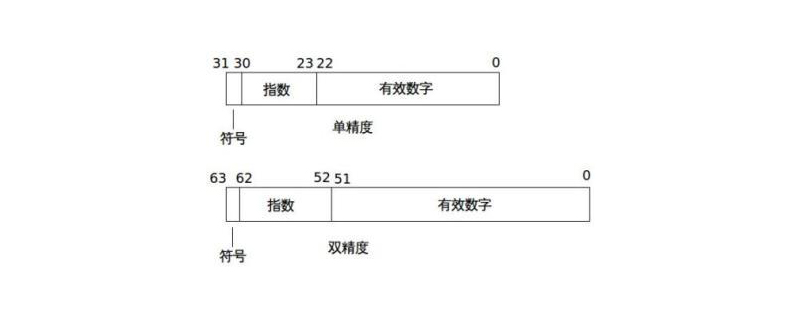
A floating point number (Floating Point Number) consists of three basic components: Sign, Exponent and Mantissa. Floating point numbers can usually be represented in the following format:

Where S is the sign bit, P is the exponent code, and M is the mantissa.

According to the definition in the IEEE (Institute of Electrical and Electronics Engineers) 754 standard, single-precision floating-point numbers are 32-bit (i.e. 4 bytes), and double-precision floating-point numbers are 64-bit (i.e. 8 bytes) of. The number of digits occupied by S, P and M and the representation method of the two are shown in the following table:

	S	P	M	Represents the formula	Offset
Single precision floating point number	1 (31st position)	8 (30th to 23rd position)	23 (22nd to 0th position)	(-1)^S2(P-127) 1.M	127
Double precision floating point number	1 (63rd bit)	11 (62 to 52 Bits)	52 (digits 51 to 0)	(-1)^S2(P-1023)1.M	1023

Among them, S is the sign bit, only 0 and 1, indicating positive and negative respectively.

P is the order code, usually represented by frame code (frame code and complement code only have the sign bit opposite, and the rest are the same. For For positive numbers, the original code, complement and complement are the same; for negative numbers, the complement is the inversion of all the original codes of their absolute values, and then adding 1). The exponent code can be a positive number or a negative number. In order to handle the case of negative exponent, the actual exponent value needs to be added with a bias (Bias) value as the value stored in the exponent field as required. The bias value of a single precision number is 127, the deviation value of the double is 1023. For example, the actual exponent value 0 of single precision will be stored as 127 in the exponent field, while 64 stored in the exponent field represents the actual exponent value -63. The introduction of the bias makes it possible for single-precision numbers to actually express the exponent value The range becomes -127 to 128 (both ends included).

M is the mantissa, where single-precision numbers are 23 bits long and double-precision numbers are 52 bits long. The IEEE standard requires that floating point numbers must be canonical. This means that the left side of the decimal point of the mantissa must be 1, so when saving the mantissa, the 1 in front of the decimal point can be omitted, thereby freeing up a binary bit to save more mantissas. This actually uses a 23-bit long mantissa field to express the 24-bit mantissa. For example, for single-precision numbers, binary 1001.101 (corresponding to decimal 9.625) can be expressed as 1.001101 × 23, so the value actually stored in the mantissa field is 00110100000000000000000, that is, the 1 on the left of the decimal point is removed, and 0 is used on the right. Complete.
According to standard requirements, values that cannot be saved accurately must be rounded to the nearest saveable value, that is, if it is less than half, it will be rounded, and if it is more than half (including half), it will be rounded. However, for binary floating point numbers, there is one more rule, that is, when the value that needs to be rounded is exactly half, it is not simply rounded, but the last one of the two storable values that are equidistantly close before and after is taken. The number of significant digits is zero.

According to the above analysis, the IEEE 754 standard defines the representation range of floating point numbers as:

	Binary (Binary)	Decimal(Decimal)
Single precision floating point number	± (2-2^-23) × 2127	~ ± 10^38.53
Double precision floating point number	± (2-2^-52) × 21023	~ ± 10^ 308.25

The representation of floating point numbers has a certain range. When it exceeds the range, an overflow (Flow) will occur. Generally speaking, data larger than the largest absolute value is called overflow (Overflow), and data smaller than the smallest absolute value is called underflow (Underflow).

Representation Conventions for Floating Point Numbers

Single-precision floating-point numbers and double-precision floating-point numbers are both defined by the IEEE 754 standard, and there are some special conventions. For example:
1. When P=0, M=0, it means 0.
　2. When P=255 and M=0, it means infinity, and the sign bit is used to determine whether it is positive infinity or negative infinity.
　3. When P=255 and M≠0, it means NaN (Not a Number, not a number).
Non-standard floating-point numbers

When two floating-point numbers with extremely small absolute values are subtracted, the exponent of the difference may exceed the allowed range, and can only be approximately 0 in the end. In order to solve such problems, the IEEE standard introduced denormalized floating-point numbers, which stipulates that when the exponent of a floating-point number is the minimum allowed exponent value, the mantissa does not have to be normalized. With non-standard floating point numbers, the implicit restriction of the mantissa bit is removed, and floating point numbers with smaller absolute values can be stored. Moreover, since it is no longer restricted by the implicit mantissa field, the above-mentioned problem about extremely small differences does not exist, because all differences between floating point numbers that can be saved can also be saved.
According to the definition in the IEEE 754 standard, the representation range of canonical and non-canonical floating point numbers can be summarized as the following table:

##Single precision floating point number± 2^-149 to (1-2^-23)*2^-126± 2^-126 to (2-2^-23)*2^127± ~10^-44.85 to ~10^38.53Double precision floating point number± 2^-1074 to (1-2^-52)*2^-1022± 2^-1022 to (2-2^-52)*2^1023± ~10^-323.3 to ~10^308.3

Canonical floating point number	Non-canonical floating point number	Decimal approximate range

Standards related to IEEE 754

The conclusion of this article is based on the IEEE 754 standard. Another standard is IEEE 854. This standard is about decimal floating point numbers, but it does not specify a specific format, so Rarely used. In addition, starting in 2000, IEEE 754 began to be revised, known as IEEE 754R, with the purpose of integrating the IEEE 754 and IEEE 854 standards. The revisions to the floating-point format of this standard include: 1. Adding 16-bit and 128-bit binary floating-point formats; 2. Adding decimal floating-point format and adopting the format proposed by IBM.

Summary: The above is the entire content of this article, I hope it will be helpful to everyone.

The above is the detailed content of Representation range of floating point numbers. For more information, please follow other related articles on the PHP Chinese website!