
In computer science, a binary tree is a tree structure with at most two subtrees per node. Usually subtrees are called "left subtree" and "right subtree". Binary trees are often used to implement binary search trees and binary heaps.
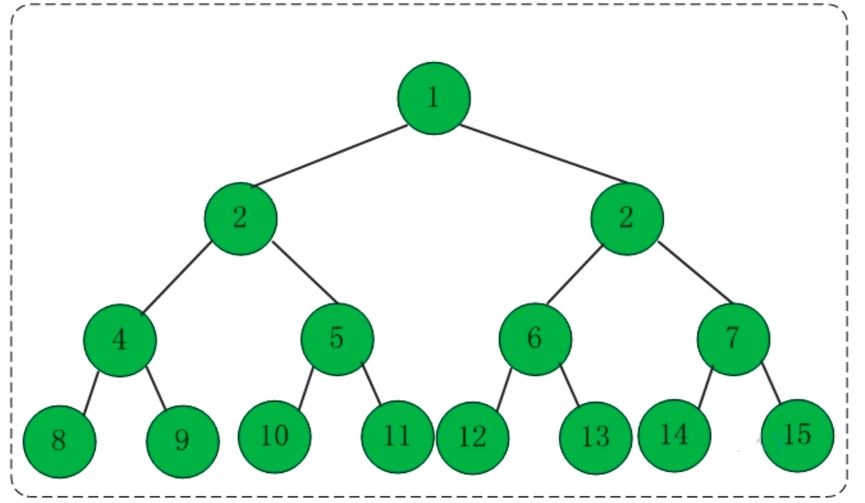
A binary tree with depth k and 2^k-1 nodes is called a full binary tree. The characteristic of this kind of tree is that the number of nodes on each level is the maximum number of nodes. In a binary tree, except for the last level, if all other levels are full, and the last level is either full or lacks several consecutive nodes on the right, then the binary tree is a complete binary tree. The depth of a complete binary tree with n nodes is floor(log2n) 1. A complete binary tree with depth k has at least 2k-1 leaf nodes and at most 2k-1 nodes.
Binary tree properties
(1) In a non-empty binary tree, the total number of nodes in the i-th level does not exceed 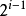 , i>=1;
, i>=1;
(2) A binary tree with depth h has at most 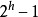 nodes (h>=1) and at least h nodes;
nodes (h>=1) and at least h nodes;
(3) For any binary tree, if it The number of leaf nodes is N0, and the total number of nodes with degree 2 is N2, then N0=N2 1;
(4) The depth of a complete binary tree with n nodes is 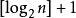 (Note: [ ] means rounding down)
(Note: [ ] means rounding down)
Recommended course: PHP Tutorial.
(5) If each node of a complete binary tree with N nodes is stored in a sequential manner, the nodes have the following relationship:
If I is the node number, then if I> ;1, then the number of its parent node is I/2;
If 2*I<=N, then the number of its left child (that is, the root node of the left subtree) is 2*I; If 2*I>N, there is no left child;
If 2*I 1<=N, then the node number of its right child is 2*I 1; if 2*I 1>N, then No right children.
(6) Given N nodes, h(N) different binary trees can be formed.
h(N) is the Nth term of Cattelan number. h(n)=C(2*n,n)/(n 1).
(7) There are i branch points, I is the sum of the road lengths of all branch points, J is the sum of the road lengths of the leaves J=I 2i [2]
Basic Concept
Binary tree is defined recursively, and its nodes are divided into left and right subtrees. Logically, binary trees have five basic forms:
(1) Empty binary tree - as shown in the figure (a);
(2) A binary tree with only one root node - as shown in (b);
(3) Only a left subtree - as shown in (c);
(4) Only the right subtree - as shown in figure (d);
(5) Complete binary tree - as shown in (e).
Note: Although binary trees have many similarities to trees, binary trees are not a special case of trees. [1]
Type
(1) Complete binary tree - If the height of the binary tree is h, except for the h-th layer, all other layers (1~h -1) The number of nodes has reached the maximum number. There are leaf nodes in layer h, and the leaf nodes are arranged from left to right. This is a complete binary tree.
(2) Full binary tree - a binary tree in which every node except leaf nodes has left and right subleaves, and the leaf nodes are all at the bottom.
(3) Balanced binary tree - A balanced binary tree is also called an AVL tree (different from the AVL algorithm). It is a binary sorting tree and has the following properties: it is an empty tree or it The absolute value of the height difference between the left and right subtrees does not exceed 1, and the left and right subtrees are both balanced binary trees.
Discrimination
Binary tree is not a special case of tree. Although it has many similarities with tree, there are two main differences between tree and binary tree:
1. There is no limit to the maximum degree of nodes in a tree, while the maximum degree of a node in a binary tree is 2;
2. There is no left or right distinction between the nodes of a tree, while the nodes of a binary tree There are left and right.
The above is the detailed content of Basic properties of binary trees. For more information, please follow other related articles on the PHP Chinese website!
 What is j2ee
What is j2ee
 Solutions to unknown software exception exceptions in computer applications
Solutions to unknown software exception exceptions in computer applications
 Introduction to the meaning of += in C language
Introduction to the meaning of += in C language
 How to install the driver
How to install the driver
 What are the main characteristics of computers?
What are the main characteristics of computers?
 MySQL password change method
MySQL password change method
 Ripple currency today's market price
Ripple currency today's market price
 modify ip
modify ip
 What are the C language programming software?
What are the C language programming software?