Binary tree formulas you must understand

1. Properties of general binary trees
Properties 1. On the i level of a non-empty binary tree, there are at most 2^i nodes .
Property 2. In a binary tree with height K, there are at most 2^(k 1)-1 nodes.
Property 3. For any non-empty binary tree, if the number of leaf nodes is n0 and the number of nodes with degree 2 is n2, then n0=n2 1.
2, Complete Binary Tree
Definition: If in a binary tree, only the degrees of the nodes at the bottom two levels are less than 2, the degrees of the nodes at all other levels are equal to 2, and the nodes of the bottom layer are concentrated in the leftmost positions of the layer, then this binary tree is called a complete binary tree.
Property 1. The height k of a complete binary tree with n nodes is [log^2n].
Property 2. For a complete binary tree with n nodes, if all the nodes in the binary tree are sequenced from top (root node) to bottom (leaf node) and from left to right, Numbering starts from 0 to n-1, then for any node whose subscript is i, there are:
(1) If i=0, it is the root node and it has no parent node; If i>0, then the subscript of its parent node is (i-1)/2.
(2) If 2i 1<=n-1, then the subscript of the left child node of the node with subscript i is 2i 1; otherwise, the node with subscript i has no left child Node.
(3) If 2i 2<=n-1, then the subscript of the right child node of the node with subscript i is 2i 2; otherwise, the node with subscript i has no right child Node.
3, Full Binary Tree
Definition: If any node of a binary tree is either a leaf, or has two non-empty subtrees, then this binary tree is called Full binary tree.
Property, in a full binary tree, the number of leaf nodes is 1 more than the number of branch nodes.
4, Expanded Binary Tree
Definition: An expanded binary tree is an expansion of an existing binary tree. After the expansion, the nodes of the original binary tree become branches with degree 2. Node. That is to say, if the degree of the original node is 2, it will remain unchanged; if the degree is 1, then one branch will be added; if the degree is 0, then two branches will be added.
Property 1. In the extended binary tree, the number of external nodes is 1 more than the number of internal nodes.
Property 2. For any extended binary tree, the following relationship is satisfied between the external path length E and the internal path length I: E=I 2n, where n is the number of internal nodes.
For more technical articles related to frequently asked questions, please visit the FAQ column to learn more!
The above is the detailed content of Binary tree formulas you must understand. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1378
1378
 52
52
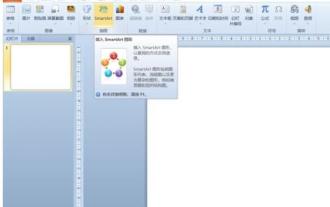 Detailed method of inserting formula effect flow chart into PPT
Mar 26, 2024 pm 04:36 PM
Detailed method of inserting formula effect flow chart into PPT
Mar 26, 2024 pm 04:36 PM
1. Open PPT, click the [Insert] tab, and click the [smartArt] button in the [Illustrations] group. 2. Click [Process] in the [Select smartArt graphics] dialog box that opens. 3. Select the [Formula] flow chart in the [Process] pane that opens. 4. Click [OK], and the [Formula] flow chart will be inserted into the slide pane. 5. Click [Text] in the [Type text here] column, or click [Text] on the graphic to enter content. 6. Select the shape in the graphic, click the [Design] tab of [smartArt Tools], and click the [Add Shape] button in the [Create Graphics] group to add a shape. 7. The shapes in the graphics can also be selected and deleted. Of course, you can also delete them in smar as needed.
 How to operate Excel table formulas
Mar 20, 2024 pm 12:07 PM
How to operate Excel table formulas
Mar 20, 2024 pm 12:07 PM
When using excel software at work, function formulas are often used. If you want to be proficient in using excel, you must be proficient in operating function formulas. It is actually not difficult to master formulas. We can start learning from the simplest ones. Today I will share with you how to operate Excel table formulas. Take the multiplication formula as an example, let's learn with you! 1. First, open excel. Since I am doing a demonstration here, I input two sets of data casually. Now we need to calculate the product of these two sets of data. We want to calculate the product of columns A and B, and put the cell at D4, as shown in the red circle in the figure below: 2. Then, enter the equal sign in the cell and select the first parameter cell B4, Enter the multiplication sign and select the second parameter C4
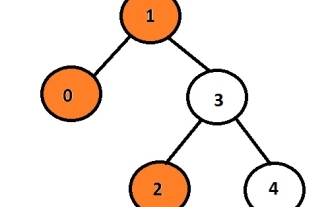 Print left view of binary tree in C language
Sep 03, 2023 pm 01:25 PM
Print left view of binary tree in C language
Sep 03, 2023 pm 01:25 PM
The task is to print the left node of the given binary tree. First, the user will insert data, thus generating a binary tree, and then print the left view of the resulting tree. Each node can have at most 2 child nodes so this program must iterate over only the left pointer associated with the node if the left pointer is not null it means it will have some data or pointer associated with it otherwise it will be printed and displayed as the left child of the output. ExampleInput:10324Output:102Here, the orange node represents the left view of the binary tree. In the given graph the node with data 1 is the root node so it will be printed and instead of going to the left child it will print 0 and then it will go to 3 and print its left child which is 2 . We can use recursive method to store the level of node
 Detailed explanation of binary tree structure in Java
Jun 16, 2023 am 08:58 AM
Detailed explanation of binary tree structure in Java
Jun 16, 2023 am 08:58 AM
Binary trees are a common data structure in computer science and a commonly used data structure in Java programming. This article will introduce the binary tree structure in Java in detail. 1. What is a binary tree? In computer science, a binary tree is a tree structure in which each node has at most two child nodes. Among them, the left child node is smaller than the parent node, and the right child node is larger than the parent node. In Java programming, binary trees are commonly used to represent sorting, searching and improving the efficiency of data query. 2. Binary tree implementation in Java In Java, binary tree
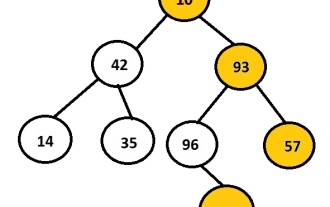 In C language, print the right view of the binary tree
Sep 16, 2023 pm 11:13 PM
In C language, print the right view of the binary tree
Sep 16, 2023 pm 11:13 PM
The task is to print the right node of the given binary tree. First the user will insert data to create a binary tree and then print a right view of the resulting tree. The image above shows a binary tree created using nodes 10, 42, 93, 14, 35, 96, 57 and 88, with the nodes on the right side of the tree selected and displayed. For example, 10, 93, 57, and 88 are the rightmost nodes of the binary tree. Example Input:1042931435965788Output:10935788 Each node has two pointers, the left pointer and the right pointer. According to this question, the program only needs to traverse the right node. Therefore, the left child of the node does not need to be considered. The right view stores all nodes that are the last node in their hierarchy. Therefore, we can
 How to implement binary tree traversal using Python
Jun 09, 2023 pm 09:12 PM
How to implement binary tree traversal using Python
Jun 09, 2023 pm 09:12 PM
As a commonly used data structure, binary trees are often used to store data, search and sort. Traversing a binary tree is one of the very common operations. As a simple and easy-to-use programming language, Python has many methods to implement binary tree traversal. This article will introduce how to use Python to implement pre-order, in-order and post-order traversal of a binary tree. Basics of Binary Trees Before learning how to traverse a binary tree, we need to understand the basic concepts of a binary tree. A binary tree consists of nodes, each node has a value and two child nodes (left child node and right child node
 How to use formula vlookup
Feb 19, 2024 pm 10:37 PM
How to use formula vlookup
Feb 19, 2024 pm 10:37 PM
The formula VLOOKUP is a very commonly used function in Microsoft Excel. It is used to find a specific value in a table or data set and return other values associated with it. In this article, we will learn how to use the VLOOKUP formula correctly. The basic syntax of the VLOOKUP function is as follows: VLOOKUP(lookup_value, table_array, col_index_num, [range_lookup]) where: lookup
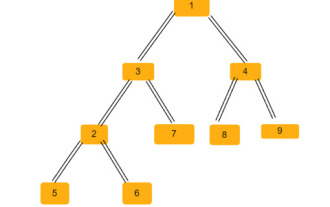 The number of isosceles triangles in a binary tree
Sep 05, 2023 am 09:41 AM
The number of isosceles triangles in a binary tree
Sep 05, 2023 am 09:41 AM
A binary tree is a data structure in which each node can have up to two child nodes. These children are called left children and right children respectively. Suppose we are given a parent array representation, you have to use it to create a binary tree. A binary tree may have several isosceles triangles. We have to find the total number of possible isosceles triangles in this binary tree. In this article, we will explore several techniques for solving this problem in C++. Understanding the problem gives you a parent array. You have to represent it in the form of a binary tree so that the array index forms the value of the tree node and the value in the array gives the parent node of that particular index. Note that -1 is always the root parent. Given below is an array and its binary tree representation. Parentarray=[0,-1,3,1,



