What problem is statistical bootstrap used to solve?
The Bootstrap method makes statistical inferences about the distribution characteristics of the population based on the given original sample copy observation information, without requiring additional information.

Efron (1979) believes that this method is also a non-parametric statistical method. (Recommended learning: Bootstrap video tutorial)
The Bootstrap method starts from the observation data and does not require any distribution assumptions. It uses the Bootstrap method to address parameter estimation and hypothesis testing problems in statistics. The data set of a certain statistic calculated by bootstrapping samples can be used to reflect the sampling distribution of the statistic, that is, to generate an empirical distribution. In this way, even if we are uncertain about the overall distribution, we can approximately estimate the statistic and its confidence interval. From this distribution, quantiles corresponding to different confidence levels can be obtained—the so-called critical values, which can be further used for hypothesis testing.
Therefore, the Bootstrap method can solve many problems that cannot be solved by traditional statistical analysis methods.
In the implementation process of Bootstrap, the status of computers cannot be ignored (Diaconis et al., 1983), because Bootstrap involves a large number of simulation calculations.
It can be said that without computers, Bootstrap theory can only be empty talk. With the rapid development of computers, the calculation speed has increased and the calculation time has been greatly reduced.
When the data distribution assumption is too far-fetched or the analytical formula is too difficult to derive, Bootstrap provides us with another effective way to solve the problem. Therefore, this method has certain utilization value and practical significance in biological research.
Reasons for applying bootstrap:
In fact, when performing analysis, the first thing to do is to determine the type of random variable, and then to determine the random variable What distribution does the data of the variable obey?
What distribution is crucial, because it directly determines whether it can be analyzed. For example: If you perform variance analysis, you must first require a normal distribution. If it is not a normal distribution, you must take remedial measures. This remedial measure is bootstrap.
bootstrap also has another use, because classic statistics is relatively perfect for central tendency, but for some other distribution parameters, such as median, quartile, standard deviation, coefficient of variation, etc. It is estimated to be imperfect, so bootstrap is needed.
bootstrap is similar to the classic statistical method. Generally, the parametric method is more efficient than the non-parametric method. However, the biggest drawback of the parametric method is that it requires a distribution model in advance. If the model does not meet the requirements, the analysis results It may be wrong, which is a white analysis.
For more technical articles related to Bootstrap, please visit the Bootstrap Tutorial column to learn!
The above is the detailed content of What problem is statistical bootstrap used to solve?. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 How to introduce bootstrap into Eclipse
Apr 05, 2024 am 02:30 AM
How to introduce bootstrap into Eclipse
Apr 05, 2024 am 02:30 AM
Introduce Bootstrap in Eclipse in five steps: Download the Bootstrap file and unzip it. Import the Bootstrap folder into the project. Add Bootstrap dependency. Load Bootstrap CSS and JS in HTML files. Start using Bootstrap to enhance your user interface.
 How to read the bootstrap mediation effect test results in stata
Apr 05, 2024 am 01:48 AM
How to read the bootstrap mediation effect test results in stata
Apr 05, 2024 am 01:48 AM
Interpretation steps of Bootstrap mediation effect test in Stata: Check the sign of the coefficient: Determine the positive or negative direction of the mediation effect. Test p value: less than 0.05 indicates that the mediating effect is significant. Check the confidence interval: not containing zero indicates that the mediation effect is significant. Comparing the median p-value: less than 0.05 further supports the significance of the mediation effect.
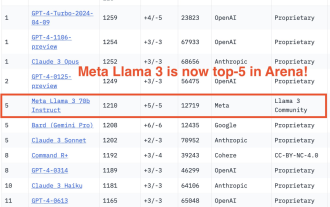 750,000 rounds of one-on-one battle between large models, GPT-4 won the championship, and Llama 3 ranked fifth
Apr 23, 2024 pm 03:28 PM
750,000 rounds of one-on-one battle between large models, GPT-4 won the championship, and Llama 3 ranked fifth
Apr 23, 2024 pm 03:28 PM
Regarding Llama3, new test results have been released - the large model evaluation community LMSYS released a large model ranking list. Llama3 ranked fifth, and tied for first place with GPT-4 in the English category. The picture is different from other benchmarks. This list is based on one-on-one battles between models, and the evaluators from all over the network make their own propositions and scores. In the end, Llama3 ranked fifth on the list, followed by three different versions of GPT-4 and Claude3 Super Cup Opus. In the English single list, Llama3 overtook Claude and tied with GPT-4. Regarding this result, Meta’s chief scientist LeCun was very happy and forwarded the tweet and
 How to introduce idea into bootstrap
Apr 05, 2024 am 02:33 AM
How to introduce idea into bootstrap
Apr 05, 2024 am 02:33 AM
Steps to introduce Bootstrap in IntelliJ IDEA: Create a new project and select "Web Application". Add "Bootstrap" Maven dependency. Create an HTML file and add Bootstrap references. Replace with the actual path to the Bootstrap CSS file. Run the HTML file to use Bootstrap styles. Tip: Use a CDN to import Bootstrap or customize HTML file templates.
 How to use bootstrap to test mediation effects
Apr 05, 2024 am 03:57 AM
How to use bootstrap to test mediation effects
Apr 05, 2024 am 03:57 AM
The Bootstrap test uses resampling technology to evaluate the reliability of the statistical test and is used to prove the significance of the mediation effect: first, calculate the confidence interval of the direct effect, indirect effect and mediation effect; secondly, calculate the significance of the mediation type according to the Baron and Kenny or Sobel method. significance; and finally estimate the confidence interval for the natural indirect effect.
 How to read the results of bootstrap mediation test
Apr 05, 2024 am 03:30 AM
How to read the results of bootstrap mediation test
Apr 05, 2024 am 03:30 AM
The Bootstrap mediation test evaluates the mediation effect by resampling the data multiple times: Indirect effect confidence interval: indicates the estimated range of the mediation effect. If the interval does not contain zero, the effect is significant. p-value: Evaluates the probability that the confidence interval does not contain zero, with values less than 0.05 indicating significant. Sample size: The number of data samples used for analysis. Bootstrap subsampling times: the number of repeated samplings (500-2000 times). If the confidence interval does not contain zero and the p-value is less than 0.05, the mediation effect is significant, indicating that the mediating variable explains the relationship between the independent and dependent variables.
 What is the difference between bootstrap and springboot
Apr 05, 2024 am 04:00 AM
What is the difference between bootstrap and springboot
Apr 05, 2024 am 04:00 AM
The main difference between Bootstrap and Spring Boot is: Bootstrap is a lightweight CSS framework for website styling, while Spring Boot is a powerful, out-of-the-box backend framework for Java web application development. Bootstrap is based on CSS and HTML, while Spring Boot is based on Java and the Spring framework. Bootstrap focuses on creating the look and feel of a website, while Spring Boot focuses on back-end functionality. Spring Boot can be integrated with Bootstrap to create fully functional, beautiful
 How to export the results of bootstrap test mediation effect stata command
Apr 05, 2024 am 03:39 AM
How to export the results of bootstrap test mediation effect stata command
Apr 05, 2024 am 03:39 AM
Export the results of the Bootstrap mediation effect test in Stata: Save the results: bootstrap post Create variable list: local vars: coef se ci Export the results (CSV): export delimited results.csv, varlist(`vars') replace comma nolabel






