What is the time complexity of recursive algorithm

The time complexity of the recursive algorithm is: [T(n)=o(f(n))], which means that as the problem size n increases, the execution time growth rate of the algorithm and f(n) The growth rate is proportional to the growth rate, which is called the asymptotic time complexity of the algorithm.

Time complexity of recursive algorithm

Time complexity:

Generally, the number of times the basic operations are repeated in the algorithm is a function f(n) of the problem size n, and then analyze the change of f(n) with n and determine the order of magnitude of T(n). Here ‘o’ is used to represent the order of magnitude and gives the time complexity of the algorithm.

T(n)=o(f(n));

It means that as the problem size n increases, the execution time growth rate of the algorithm is proportional to the growth rate of f(n) , which is called the asymptotic time complexity of the algorithm. And we generally discuss worst-case time complexity.

Recommended course: C language tutorial

Space complexity:

The space complexity of the algorithm is not actually occupied space, but to calculate the number of auxiliary space units in the entire algorithm space, which has nothing to do with the scale of the problem. The space complexity S(n) of an algorithm is defined as the order of magnitude of the space consumed by the algorithm.

S(n)=o(f(n))

If the auxiliary space required for algorithm execution is a constant relative to the input data n, it is called the space complexity of the algorithm The auxiliary space is o (1);

The space complexity of the recursive algorithm: the recursion depth n*the auxiliary space required for each recursion. If the auxiliary space required for each recursion is a constant, the recursion space complexity is o (n).

The calculation equation of the time complexity of the recursive algorithm is a recursive equation:

You can consider an example before introducing the recursive tree:

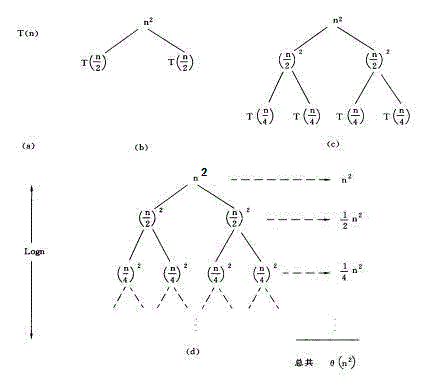
T(n) = 2T(n/2) + n2

Iterate 2 times to get:

T(n) = n2 + 2(2T(n/4) + (n/2) 2)

You can continue to iterate and fully expand it to get:

T(n) = n2 + 2((n/2) 2 +
2((n/22)2 + 2((n/23) 2 +
2((n/24) 2 +…+2((n/2i) 2 +
2T(n/2i + 1)))…))))……(1)

And when n/2i 1 == 1, Iteration ends.

Expand the parentheses of formula (1), we can get:

T(n) = n2 + 2(n/2)2 +
22(n/22) 2 + … + 2i(n/2i)2 +
2i+1T(n/2i+1)

This happens to be a tree structure, from which the recursive tree method can be derived.

(a)(b)(c)(d) in the figure are the 1st, 2nd, 3rd, and nth steps of the recursive tree generation respectively. In each node, the current free item n2 is retained, and the two recursive items T(n/2)
T(n/2) are allocated to its two child nodes respectively, and so on.

The sum of all nodes in the graph is:

[1 + 1/2 + (1/2)2 + (1/2)3 + … + (1/2)i] n2 = 2n2

It can be seen that its time complexity is O(n2)

The rule of the recursive tree can be obtained as :

(1) The nodes of each layer are T(n) = kT(n / m) The value of f(n) in f(n) under the current n/m;

(2) The number of branches of each node is k;

(3) The right side of each layer marks the sum of all nodes in the current layer.

Another example:

T(n) = T(n/3) T(2n/3) n

its recursive tree As shown in the figure below:

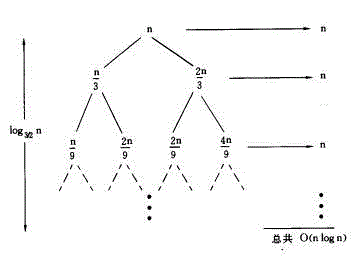
It can be seen that the value of each layer is n, and the longest path from the root to the leaf node is:

Because the final recursive The stop is at (2/3)kn == 1. Then

then

##that is,

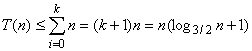
T(n) = O( nlogn)　

Summary, use this method to solve the complexity of the recursive algorithm:

f(n) = af(n/b) + d(n)

1. When d(n) is a constant:

　

2. When d(n) = cn:

3. When d(n) is other situations, the recursion tree can be used for analysis .

From the second case, if the divide-and-conquer method is used to improve the original algorithm, the focus is to use new calculation methods to reduce the value of a.

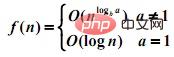
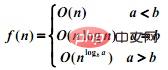
The above is the detailed content of What is the time complexity of recursive algorithm. For more information, please follow other related articles on the PHP Chinese website!