 Common Problem
Common Problem
 The in-order traversal sequence of a certain binary tree is cbade, and the pre-order traversal sequence is
The in-order traversal sequence of a certain binary tree is cbade, and the pre-order traversal sequence is
The in-order traversal sequence of a certain binary tree is cbade, and the pre-order traversal sequence is
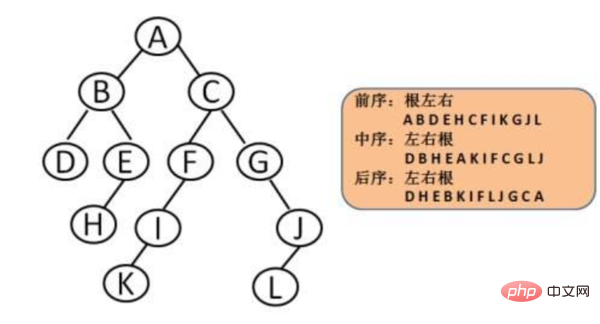
The in-order traversal sequence of a certain binary tree is CBADE, the post-order traversal sequence is CBADE, and the pre-order traversal sequence is EDABC.
First of all, post-order traversal means to first visit the left and right child nodes of the parent node, and finally visit the parent node.
Therefore, the last element of the postorder traversal sequence is the root node of the binary tree, which is E, so CBAD is the descendant node of E. (Recommended learning: web front-end video tutorial)
Now continue to look at in-order traversal. In-order traversal means that the left child of the parent node is visited first, then the parent node is visited, and finally Right child.
So the CBAD on the left side of root node E is its left child, and it has no right child. Then go back to the post-order traversal sequence again, because we already know that E is the root node, so we only need to consider CBAD.
So D is the direct left child of E, that is, D is the root node of the left subtree. Then continue to check the in-order traversal, you can find that D has no right subtree, only the left child CBA.
By analogy, it can be found that all nodes of this binary tree have no right children, and they are EDABC from top to bottom, so the preorder traversal is EDABC.
Characteristics of binary trees:
1. Each node has at most two subtrees, so there is no degree greater than 2 node.
2. The left subtree and the right subtree are in order, and the order cannot be reversed arbitrarily.
3. Even if a node in the tree has only one subtree, it must be distinguished whether it is a left subtree or a right subtree.
The above is the detailed content of The in-order traversal sequence of a certain binary tree is cbade, and the pre-order traversal sequence is. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1378
1378
 52
52
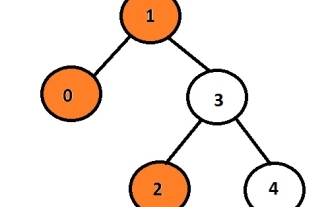 Print left view of binary tree in C language
Sep 03, 2023 pm 01:25 PM
Print left view of binary tree in C language
Sep 03, 2023 pm 01:25 PM
The task is to print the left node of the given binary tree. First, the user will insert data, thus generating a binary tree, and then print the left view of the resulting tree. Each node can have at most 2 child nodes so this program must iterate over only the left pointer associated with the node if the left pointer is not null it means it will have some data or pointer associated with it otherwise it will be printed and displayed as the left child of the output. ExampleInput:10324Output:102Here, the orange node represents the left view of the binary tree. In the given graph the node with data 1 is the root node so it will be printed and instead of going to the left child it will print 0 and then it will go to 3 and print its left child which is 2 . We can use recursive method to store the level of node
 Detailed explanation of binary tree structure in Java
Jun 16, 2023 am 08:58 AM
Detailed explanation of binary tree structure in Java
Jun 16, 2023 am 08:58 AM
Binary trees are a common data structure in computer science and a commonly used data structure in Java programming. This article will introduce the binary tree structure in Java in detail. 1. What is a binary tree? In computer science, a binary tree is a tree structure in which each node has at most two child nodes. Among them, the left child node is smaller than the parent node, and the right child node is larger than the parent node. In Java programming, binary trees are commonly used to represent sorting, searching and improving the efficiency of data query. 2. Binary tree implementation in Java In Java, binary tree
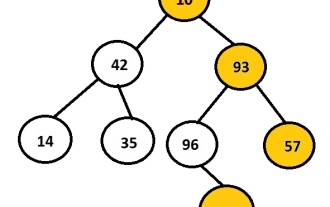 In C language, print the right view of the binary tree
Sep 16, 2023 pm 11:13 PM
In C language, print the right view of the binary tree
Sep 16, 2023 pm 11:13 PM
The task is to print the right node of the given binary tree. First the user will insert data to create a binary tree and then print a right view of the resulting tree. The image above shows a binary tree created using nodes 10, 42, 93, 14, 35, 96, 57 and 88, with the nodes on the right side of the tree selected and displayed. For example, 10, 93, 57, and 88 are the rightmost nodes of the binary tree. Example Input:1042931435965788Output:10935788 Each node has two pointers, the left pointer and the right pointer. According to this question, the program only needs to traverse the right node. Therefore, the left child of the node does not need to be considered. The right view stores all nodes that are the last node in their hierarchy. Therefore, we can
 How to implement binary tree traversal using Python
Jun 09, 2023 pm 09:12 PM
How to implement binary tree traversal using Python
Jun 09, 2023 pm 09:12 PM
As a commonly used data structure, binary trees are often used to store data, search and sort. Traversing a binary tree is one of the very common operations. As a simple and easy-to-use programming language, Python has many methods to implement binary tree traversal. This article will introduce how to use Python to implement pre-order, in-order and post-order traversal of a binary tree. Basics of Binary Trees Before learning how to traverse a binary tree, we need to understand the basic concepts of a binary tree. A binary tree consists of nodes, each node has a value and two child nodes (left child node and right child node
 The number of isosceles triangles in a binary tree
Sep 05, 2023 am 09:41 AM
The number of isosceles triangles in a binary tree
Sep 05, 2023 am 09:41 AM
A binary tree is a data structure in which each node can have up to two child nodes. These children are called left children and right children respectively. Suppose we are given a parent array representation, you have to use it to create a binary tree. A binary tree may have several isosceles triangles. We have to find the total number of possible isosceles triangles in this binary tree. In this article, we will explore several techniques for solving this problem in C++. Understanding the problem gives you a parent array. You have to represent it in the form of a binary tree so that the array index forms the value of the tree node and the value in the array gives the parent node of that particular index. Note that -1 is always the root parent. Given below is an array and its binary tree representation. Parentarray=[0,-1,3,1,
 Detailed explanation of Java binary tree implementation and specific application cases
Jun 15, 2023 pm 11:03 PM
Detailed explanation of Java binary tree implementation and specific application cases
Jun 15, 2023 pm 11:03 PM
Detailed explanation of Java binary tree implementation and specific application cases. Binary tree is a data structure often used in computer science and can perform very efficient search and sort operations. In this article, we will discuss how to implement a binary tree in Java and some of its specific application cases. Definition of Binary Tree Binary tree is a very important data structure, consisting of the root node (the top node of the tree) and several left subtrees and right subtrees. Each node has at most two child nodes, the child node on the left is called the left subtree, and the child node on the right is called the right subtree. If the node does not have
 Binary tree algorithm in PHP and FAQs
Jun 09, 2023 am 09:33 AM
Binary tree algorithm in PHP and FAQs
Jun 09, 2023 am 09:33 AM
With the continuous development of web development, PHP, as a widely used server scripting language, its algorithms and data structures are becoming more and more important. Among these algorithms and data structures, the binary tree algorithm is a very important concept. This article will introduce the binary tree algorithm and its applications in PHP, as well as answers to common questions. What is a binary tree? A binary tree is a tree structure in which each node has at most two child nodes, a left child node and a right child node. If a node has no child nodes, it is called a leaf node. Binary trees are often used for searching
 Methods and applications of binary tree implementation in PHP
Jun 18, 2023 pm 06:28 PM
Methods and applications of binary tree implementation in PHP
Jun 18, 2023 pm 06:28 PM
In computer science, a binary tree is an important data structure. It consists of nodes and the edges pointing to them, with each node connecting up to two child nodes. Binary trees are widely used in fields such as search algorithms, compilers, databases, and memory management. Many programming languages support the implementation of binary tree data structures, PHP being one of them. This article will introduce how PHP implements binary trees and its applications. Definition of Binary Tree A binary tree is a data structure that consists of nodes and edges pointing to them. Each node is connected to at most two child nodes,


