What is the difference between time-varying systems and time-invariant systems?

The difference between time-varying systems and time-invariant systems: one or more parameter values ​​in a time-varying system change with time, so the entire characteristics also change with time; while the properties of a time-invariant system are It does not change with time. The behavior of the system response only depends on the behavior of the input signal and the characteristics of the system, and has nothing to do with the time when the input signal is applied.

The operating environment of this tutorial: Windows 7 system, Dell G3 computer.

According to whether the system contains components whose parameters change with time, automatic control systems can be divided into two categories: time-varying systems and steady systems.

The stationary system is also called a time-invariant system, which is characterized by: The system's own properties (the essential properties of the object being studied, such as mass, moment of inertia, etc.)Does not change over time. Specifically, the behavior of the system response only depends on the behavior of the input signal and the characteristics of the system, and has nothing to do with the moment when the input signal is applied. That is, if the input u(t) produces the output y(t), then when the input is delayed After τ is applied to the system, the output produced by u(t-τ) is y(t-τ).

---

Steady system is also called a time-invariant system

That is: the properties of the system do not change with time And change. Specifically, the behavior of the system response only depends on the behavior of the input signal and the characteristics of the system, and has nothing to do with the moment when the input signal is applied. That is to say, if I input u at time t1, the output is y, then if I input u at time t2, the output value will still be y

---

Time-varying system

A system in which one or more parameter values ​​change over time, and thus the entire characteristics also change over time.

The rocket is a typical example of a time-varying system. During flight, its mass will decrease over time due to the consumption of fuel; another common example is a manipulator, which is in motion. The moment of inertia of each joint around the corresponding axis is a complex function with time as the independent variable.

---

Time-invariant system is a system whose output does not change directly with time.

If the input signalproduces the output y(t), then for any time delay of the inputwill get the output of the same time delay.

If the transfer function of the system is not a function of time, this characteristic can be satisfied. This feature can also be described in schematic terms

If a system is time-invariant, then the system block diagram and the block diagram at any time delay are interchangeable .

To show how to determine whether a system is time-invariant, let’s look at two systems:

System A:

##System B:

##Since system A explicitly depends on

t in addition to x(t) and y(t), it is a time-varying system, while system B does not explicitly depend on time t So it is time-invariant.

---

Mathematical analysis:

Assume that the input of a certain system is u(t) and the corresponding output is y(t).

After the input has been delayed by τ, that is, when the input is u(t-τ), if the output is also delayed by τ accordingly, that is, the output is y(t-τ), Then this system is a steady system.
That is, when the input signal u(t) is first time-shifted τ to u(t-τ), and then the system transformation H[▪] is performed to obtain the value H[u(t-τ)];

To put it bluntly, a system runs for a period of time T from the initial moment, and the input and output during this period have a corresponding trajectory.

If the state of this system at time T is re-run for a period of time T from the initial time, the input change form from the initial time is the same as before, take a look Is the output the same as before?

(For example, taking a rocket as an example, the input refers to the energy of the push, and the output refers to the acceleration;

The first time the rocket is launched under normal conditions, when running for T time, a three-dimensional curve Q1 can be drawn by inputting energy, acceleration and time;

The second rocket is launched in the same state as the first time at T time. When running for T time (the change of input energy with time is the same as the first time), at this time, the input energy and acceleration output , and the time change to draw another three-dimensional curve Q2. The two curves Q1 and Q2 do not overlap in the output acceleration (it will definitely change because the mass at time T becomes smaller))

The input signal u(t) is first subjected to system transformation H[▪] to obtain y(t), and then the value y(t-τ) obtained by time shift is equal to H[u(t-τ) )]=y(t-τ).
For example:
1. Determine whether the system y(t)=cos[u(t)], t>0 is a time-invariant system:
1). Input signal u(t), proceed first The time shift is u(t-τ), and then the value obtained by system transformation is cos[u(t-τ)], t>0;
2). Input signal u(t), first perform system transformation as cos[u(t)], and then the value obtained by time shifting is cos[u(t-τ)], t>0;
are equal, so the system is a time-invariant system.
2. Determine whether the system y(t)=u(t)▪cost is a time-invariant system:
1). Input the signal u(t), first perform a time shift to u(t-τ), The value obtained by the system transformation is u(t-τ)▪cost, t>0;
2). Input signal u(t), first perform system transformation to u(t)▪cost, and then perform time shift The obtained value is u(t-τ)▪cos(t-τ), t>0;
u(t-τ)▪cost≠u(t-τ)▪cos(t-τ), so the The system is a time-varying system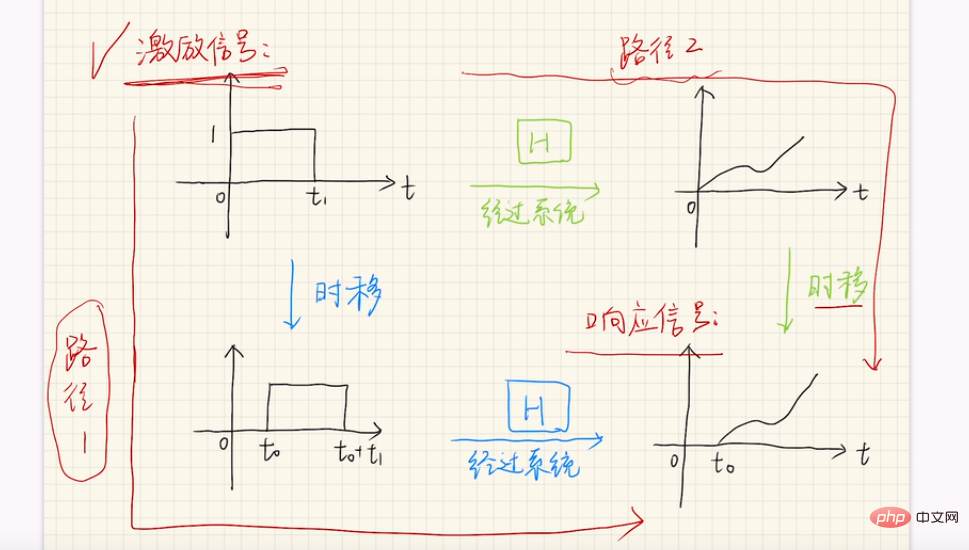

What we ultimately look at is whether the final images of the two paths (i.e. the image in the lower right corner) overlap.

Note: The above analysis method can also be used to test whether it is a steady system using the method I mentioned, that is: assuming u is input at t1, the output is y, and u is input at t2, and the output is Just check whether the value is still y

The above is the detailed content of What is the difference between time-varying systems and time-invariant systems?. For more information, please follow other related articles on the PHP Chinese website!