An in-depth analysis of quick sort in JavaScript

Introduction

Sorting refers to arranging the elements of a linear list in a specific order (numeric or alphabetical). Sorting is often used in conjunction with search.

There are many sorting algorithms, and one of the fastest by far is Quicksort(Quicksort).

Quicksort sorts the given list elements using the divide-and-conquer strategy. This means that the algorithm breaks the problem into subproblems until the subproblems become simple enough to be solved directly.

Algorithmically, this can be achieved using recursion or looping. But for this problem, it is more natural to use recursion.

Understand the logic behind quick sort

First look at how quick sort works:

1. Select an element in the array, this element is called Benchmark(Pivot). Usually the first or last element in the array is used as the basis.
2. Then, rearrange the elements of the array so that all elements to the left of the pivot are smaller than the pivot, and all elements to the right are greater than the pivot. This step is called Partitioning. If an element is equal to the base, it doesn't matter which side it is on.
3. Repeat this process for the left and right sides of the benchmark until the array is sorted.

Next, understand these steps through an example. Suppose there is an array containing unsorted elements [7, -2, 4, 1, 6, 5, 0, -4, 2]. Select the last element as the base. The decomposition steps of the array are shown in the figure below:

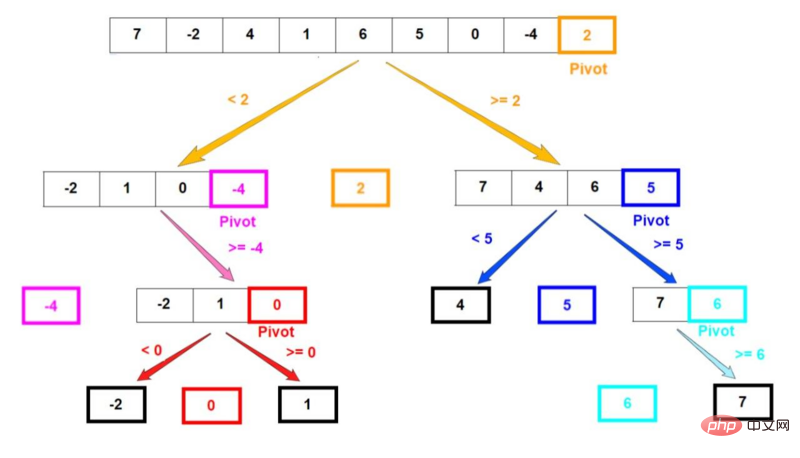
The elements selected as the basis in step 1 of the algorithm are colored. After partitioning, the base element is always at the correct position in the array.

The array with a bold black border represents what it will look like at the end of that particular recursive branch, with the resulting array containing only one element.

Finally you can see the sorting of the results of the algorithm.

Use JavaScript to implement quick sort

The backbone of this algorithm is the "partitioning" step. Whether using recursion or looping, this step is the same.

It is precisely because of this feature that the code for array partitioning is first written partition():

function partition(arr, start, end){
    // 以最后一个元素为基准
    const pivotValue = arr[end];
    let pivotIndex = start; 
    for (let i = start; i < end; i++) {
        if (arr[i] < pivotValue) {
        // 交换元素
        [arr[i], arr[pivotIndex]] = [arr[pivotIndex], arr[i]];
        // 移动到下一个元素
        pivotIndex++;
        }
    }
    
    // 把基准值放在中间
    [arr[pivotIndex], arr[end]] = [arr[end], arr[pivotIndex]] 
    return pivotIndex;
};

The code is based on the last element and uses the variable pivotIndex to track the "middle" position where all elements to the left are smaller than pivotValue and elements to the right are larger than pivotValue.

The final step swaps the pivot (last element) with pivotIndex.

Recursive implementation

After implementing the partition() function, we must solve the problem recursively and apply partitioning logic to complete the remaining steps:

function quickSortRecursive(arr, start, end) {
    // 终止条件
    if (start >= end) {
        return;
    }
    
    // 返回 pivotIndex
    let index = partition(arr, start, end);
    
    // 将相同的逻辑递归地用于左右子数组
    quickSort(arr, start, index - 1);
    quickSort(arr, index + 1, end);
}

In this function, the array is first partitioned, and then the left and right subarrays are partitioned. As long as this function receives an array that is not empty or has more than one element, the process will be repeated.

Empty arrays and arrays containing only one element are considered sorted.

Finally use the following example to test:

array = [7, -2, 4, 1, 6, 5, 0, -4, 2]
quickSortRecursive(array, 0, array.length - 1)

console.log(array)

Output:

-4,-2,0,1,2,4,5,6,7

Loop implementation

The recursive method of quick sort is more intuitive. But using loops to implement quick sort is a relatively common interview question.

Like most recursive to loop conversion solutions, the first thing that comes to mind is to use a stack to simulate recursive calls. Doing this allows you to reuse some familiar recursive logic and use it in loops.

We need a way to keep track of the remaining unsorted subarrays. One approach is to simply keep "pairs" of elements on the stack that represent the start and end of a given unsorted subarray.

JavaScript does not have an explicit stack data structure, but arrays support the push() and pop() functions. However, the peek() function is not supported, so you must use stack [stack.length-1] to manually check the top of the stack.

We will use the same "partitioning" function as the recursive method. Take a look at how to write the Quicksort part:

function quickSortIterative(arr) {
    // 用push()和pop()函数创建一个将作为栈使用的数组
    stack = [];
    
    // 将整个初始数组做为“未排序的子数组”
    stack.push(0);
    stack.push(arr.length - 1);
    
    // 没有显式的peek()函数
    // 只要存在未排序的子数组，就重复循环
    while(stack[stack.length - 1] >= 0){
        
        // 提取顶部未排序的子数组
        end = stack.pop();
        start = stack.pop();
        
        pivotIndex = partition(arr, start, end);
        
        // 如果基准的左侧有未排序的元素，
        // 则将该子数组添加到栈中，以便稍后对其进行排序
        if (pivotIndex - 1 > start){
            stack.push(start);
            stack.push(pivotIndex - 1);
        }
        
        // 如果基准的右侧有未排序的元素，
        // 则将该子数组添加到栈中，以便稍后对其进行排序
        if (pivotIndex + 1 < end){
            stack.push(pivotIndex + 1);
            stack.push(end);
        }
    }
}

Here is the test code:

ourArray = [7, -2, 4, 1, 6, 5, 0, -4, 2]
quickSortIterative(ourArray)

console.log(ourArray)

Output:

-4,-2,0,1,2,4,5,6,7

Visual demonstration

When it comes to sorting algorithms, Visualizing them can help us intuitively understand how they work. The following example is taken from Wikipedia:

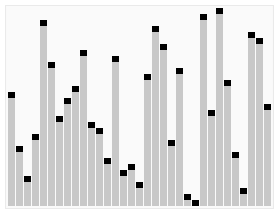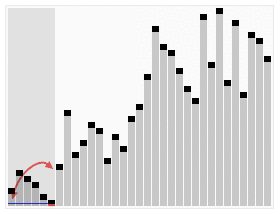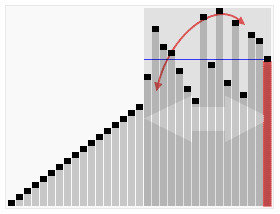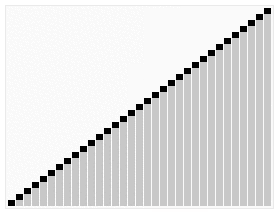
The last element in the figure is also used as a benchmark. Given an array partitioned, recursively traverse the left side until it is completely sorted. Then sort the right side.

Efficiency of quick sort

Now discuss its time and space complexity. The worst-case time complexity of quick sort is $O(n^2)$. The average time complexity is $O(n\log n)$. Typically, worst-case scenarios can be avoided by using a randomized version of quicksort.

The weakness of the quicksort algorithm is the choice of benchmark. Each time you choose a wrong pivot (a pivot larger or smaller than most elements) you will get the worst possible time complexity. When repeatedly selecting a basis, if the element value is smaller or larger than the element's basis, the time complexity is $O(n\log n)$.

It can be observed from experience that no matter which data benchmark selection strategy is adopted, the time complexity of quick sort tends to have $O(n\log n)$.

Quicksort does not take up any additional space (excluding space reserved for recursive calls). This algorithm is called the in-place algorithm and requires no extra space.

For more programming-related knowledge, please visit: Introduction to Programming! !

The above is the detailed content of An in-depth analysis of quick sort in JavaScript. For more information, please follow other related articles on the PHP Chinese website!