Algorithm learning - Java implements the longest common subsequence

实验目的:
输入两个相同类型的序列,用动态规划方法计算他们的最长公共子序列的长度以及序列。
(推荐教程:java视频教程)
思路:
1、先用一个二维数组存储最长公共子序列的长度,还要记录每个值的状态
2、根据记录值的状态,递归回溯求出最长公共子序列
3、递归方程:
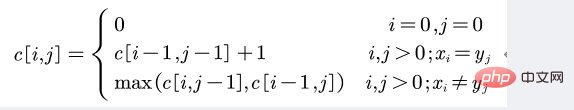
代码实现:
package c最长公共子序列;
import java.util.Scanner;
/**
* @author Draco
* @see 最长公共子序列(Longest common subsequence)
* @version
* @date-time 2020-04-27 - 下午4:23:36
*/
public class LCS {
public static void main(String[] args) {
// 测试字符串:ABCBDAB BDCABA
Scanner scanner = new Scanner(System.in);
System.out.println("注意:第一个串要长于第二个串");
System.out.print("请输入第一个字符串:");
String string1 = scanner.next();
System.out.print("请输入第二个字符串:");
String string2 = scanner.next();
String str1 = string1;
String str2 = string2;
// String str1 = "ABCBDAB";
// String str2 = "BDCABA";
int[][] c = getSubstringMatrix(str1, str2);
String[][] b = getTrace(str1, str2);
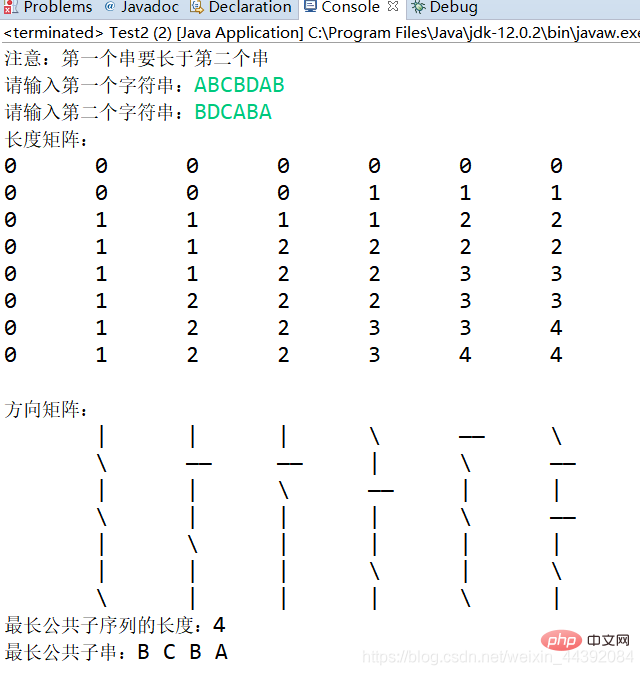
System.out.println("长度矩阵:");
show(c);
System.out.println();
System.out.println("方向矩阵:");
showForString(b);
System.out.println("最长公共子序列的长度:" + c[str1.length()][str2.length()]);
String sMax = str1.length() > str2.length() ? str1 : str2; // 选择最长的串,因为要取出最大子串
String sMin = str1.length() < str2.length() ? str1 : str2; // 选择最小的串
System.out.print("最长公共子串:");
print(b, sMax, sMax.length(), sMin.length());
}
/**
* @see 找出子序列的矩阵,其中最后一行,最后一列就是最长子序列的的长度
* @param x 第一个字符串
* @param y 第二个字符串
* @return 长度矩阵
*/
public static int[][] getSubstringMatrix(String x, String y) {
int xLen = x.length() + 1; // 加1是因为初始化第一个为0
int yLen = y.length() + 1;
int rLen = xLen > yLen ? xLen : yLen; // 大的串置为行
int cLen = xLen < yLen ? xLen : yLen; // 小的串置为列
int[][] c = new int[rLen][cLen]; // 矩阵c保存状态
for (int i = 1; i < rLen; i++) {
for (int j = 1; j < cLen; j++) {
if (x.charAt(i - 1) == y.charAt(j - 1)) {
// 相等,由斜对角线+1
c[i][j] = c[i - 1][j - 1] + 1;
} else if (c[i - 1][j] >= c[i][j - 1]) {
// 不相等,选取较大的
c[i][j] = c[i - 1][j];
} else {
c[i][j] = c[i][j - 1];
}
}
}
return c; // 长度矩阵
}
/**
* @see 记录每个值的状态,这样方便后面的回溯递归
* @param x 第一个字符串
* @param y 第二个字符串
* @return 方向矩阵
*/
public static String[][] getTrace(String x, String y) {
int xLen = x.length() + 1;
int yLen = y.length() + 1;
// 给矩阵c和b设置行和列
int rLen = xLen > yLen ? xLen : yLen;// 大的串置为行
int cLen = xLen < yLen ? xLen : yLen;// 小的串置为列
int[][] c = new int[rLen][cLen];
String[][] b = new String[rLen][cLen];
for (int i = 1; i < rLen; i++) {
for (int j = 1; j < cLen; j++) {
if (x.charAt(i - 1) == y.charAt(j - 1)) {// 相等
c[i][j] = c[i - 1][j - 1] + 1;
b[i][j] = "\\\\";// 指向左上角
} else if (c[i - 1][j] >= c[i][j - 1]) {// 不相等
// 当上面的数值大
c[i][j] = c[i - 1][j];
b[i][j] = "|";// 指向上边
} else {
// 当下面的数值大
c[i][j] = c[i][j - 1];
b[i][j] = "——";// 指向左边
}
}
}
return b;// 方向矩阵
}
/**
* @see 递归实现回溯,然后打印出最长公共子序列
* @param b 方向矩阵
* @param s 较长的字符串
* @param i 较长串的长度
* @param j 较短串的长度
*/
public static void print(String[][] b, String s, int i, int j) {
// 递归终止的条件
if (i == 0 || j == 0) {
return;
}
// 判断递归进行的条件
if (b[i][j].equals("\\\\")) {
// 遇到斜线,递归到左上角
print(b, s, i - 1, j - 1);
System.out.print(s.charAt(i - 1) + " ");
} else if (b[i][j].equals("|")) {
// 遇到竖线,递归到上边
print(b, s, i - 1, j);
} else if (b[i][j].equals("——")) {
// 遇到横线,递归到左边
print(b, s, i, j - 1);
}
}
/**
* @see 打印二维数组
* @param b 一个二维数组
*/
public static void show(int[][] b) {
for (int w = 0; w < b.length; w++) {
for (int p = 0; p < b[w].length; p++) {
System.out.print(b[w][p] + "\\t");
if (p == b[w].length - 1) {
System.out.println();
}
}
}
}
/**
* @see 打印字符串的二维数组
* @param b 一个字符串的二位数组
*/
public static void showForString(String[][] b) {
for (int w = 1; w < b.length; w++) {
System.out.print("\\t");
for (int p = 1; p < b[w].length; p++) {
System.out.print(b[w][p] + "\\t");
if (p == b[w].length - 1) {
System.out.println();
}
}
}
}
}运行结果:
相关推荐:java入门
The above is the detailed content of Algorithm learning - Java implements the longest common subsequence. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1386
1386
 52
52
 Perfect Number in Java
Aug 30, 2024 pm 04:28 PM
Perfect Number in Java
Aug 30, 2024 pm 04:28 PM
Guide to Perfect Number in Java. Here we discuss the Definition, How to check Perfect number in Java?, examples with code implementation.
 Weka in Java
Aug 30, 2024 pm 04:28 PM
Weka in Java
Aug 30, 2024 pm 04:28 PM
Guide to Weka in Java. Here we discuss the Introduction, how to use weka java, the type of platform, and advantages with examples.
 Smith Number in Java
Aug 30, 2024 pm 04:28 PM
Smith Number in Java
Aug 30, 2024 pm 04:28 PM
Guide to Smith Number in Java. Here we discuss the Definition, How to check smith number in Java? example with code implementation.
 Java Spring Interview Questions
Aug 30, 2024 pm 04:29 PM
Java Spring Interview Questions
Aug 30, 2024 pm 04:29 PM
In this article, we have kept the most asked Java Spring Interview Questions with their detailed answers. So that you can crack the interview.
 Break or return from Java 8 stream forEach?
Feb 07, 2025 pm 12:09 PM
Break or return from Java 8 stream forEach?
Feb 07, 2025 pm 12:09 PM
Java 8 introduces the Stream API, providing a powerful and expressive way to process data collections. However, a common question when using Stream is: How to break or return from a forEach operation? Traditional loops allow for early interruption or return, but Stream's forEach method does not directly support this method. This article will explain the reasons and explore alternative methods for implementing premature termination in Stream processing systems. Further reading: Java Stream API improvements Understand Stream forEach The forEach method is a terminal operation that performs one operation on each element in the Stream. Its design intention is
 TimeStamp to Date in Java
Aug 30, 2024 pm 04:28 PM
TimeStamp to Date in Java
Aug 30, 2024 pm 04:28 PM
Guide to TimeStamp to Date in Java. Here we also discuss the introduction and how to convert timestamp to date in java along with examples.
 Java Program to Find the Volume of Capsule
Feb 07, 2025 am 11:37 AM
Java Program to Find the Volume of Capsule
Feb 07, 2025 am 11:37 AM
Capsules are three-dimensional geometric figures, composed of a cylinder and a hemisphere at both ends. The volume of the capsule can be calculated by adding the volume of the cylinder and the volume of the hemisphere at both ends. This tutorial will discuss how to calculate the volume of a given capsule in Java using different methods. Capsule volume formula The formula for capsule volume is as follows: Capsule volume = Cylindrical volume Volume Two hemisphere volume in, r: The radius of the hemisphere. h: The height of the cylinder (excluding the hemisphere). Example 1 enter Radius = 5 units Height = 10 units Output Volume = 1570.8 cubic units explain Calculate volume using formula: Volume = π × r2 × h (4
 Create the Future: Java Programming for Absolute Beginners
Oct 13, 2024 pm 01:32 PM
Create the Future: Java Programming for Absolute Beginners
Oct 13, 2024 pm 01:32 PM
Java is a popular programming language that can be learned by both beginners and experienced developers. This tutorial starts with basic concepts and progresses through advanced topics. After installing the Java Development Kit, you can practice programming by creating a simple "Hello, World!" program. After you understand the code, use the command prompt to compile and run the program, and "Hello, World!" will be output on the console. Learning Java starts your programming journey, and as your mastery deepens, you can create more complex applications.




