
The traversal method of in-order traversal is: for the current node, first traverse the left subtree, then visit the current node, and finally traverse the right subtree. In-order traversal is a type of binary tree traversal, also called mid-root traversal and in-order tour.

The operating environment of this tutorial: Windows 7 system, C 17 version, Dell G3 computer.
Binary tree is an important data structure, and traversing the binary tree is also very important. Here we briefly introduce three methods of in-order traversal of binary trees. In-order traversal of a binary tree first traverses the left subtree, then visits the current node, and finally traverses the right subtree. For the following binary tree, the in-order traversal result is as follows:
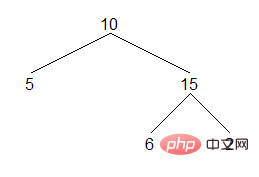
Result: [5,10,6,15,2]
Intuitively See, in-order traversal of a binary tree is to project the nodes onto a horizontal coordinate. As shown in the picture:
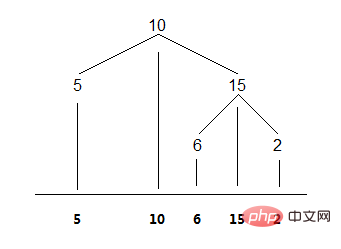
1. Recursive method
This is the simplest method, easy to think of and easy to implement. The termination condition of recursion is whether the current node is empty. First the recursive call traverses the left subtree, then visits the current node, and finally the right subtree is called recursively. The code is as follows:
//recursive
class Solution1 {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> ret;
if(root==NULL)return ret;
inorderHelper(ret,root);
return ret;
}
private:
void inorderHelper(vector<int>& ret,TreeNode* root)
{
if(root==NULL)return;
inorderHelper(ret,root->left);
ret.push_back(root->val);
inorderHelper(ret,root->right);
}
};2. Iterative method
In the iterative method, start from the root node to find the leftmost node of the binary tree, save the passed nodes in a stack, and find the leftmost node. After visiting the node, for each node, it is the root node of the subtree with itself as the root. After the visit, you can go to the right child. The code is as follows:
//iterate,using a stack
class Solution2 {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> ret;
if(root==NULL)return ret;
TreeNode *curr=root;
stack<TreeNode*> st;
while(!st.empty()||curr!=NULL)
{
while(curr!=NULL)
{
st.push(curr);
curr=curr->left;
}
curr=st.top();
st.pop();
ret.push_back(curr->val);
curr=curr->right;
}
return ret;
}
};The time complexity of this method is O(n), and the space complexity is also O(n).
3. Morris Method
This method was invented by Morris. After reading it, I feel it is extremely exquisite. This method does not use recursion, does not use the stack, and completes the binary tree traversal with O(1) space complexity. The basic idea of this method is to point the right son of all nodes whose right son is NULL to the successor node (for nodes whose right son is not null, the right son is the node to be visited next). In this way, for any node, after accessing it, its right son has pointed to the next node to be visited. For the rightmost node, no such operation is required. Note that this operation is completed during traversal, and the tree will be restored after completing the node access. The judgment condition of the entire loop is whether the current node is empty. For example, in the binary tree above, the traversal process is as follows (based on the position of the current node c):
(1) The current node is 10, because the left son is not empty and cannot be accessed. Find the rightmost node of the left subtree of c p:
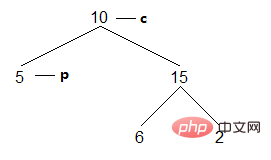
Result: []
(2) There are two termination conditions for finding the rightmost node of the left subtree of node c, One right son is empty, one right son points to the current node. The following is the case where the right son is empty. This case needs to be constructed first, pointing the right son of node p to the successor node c, and then moving c down:
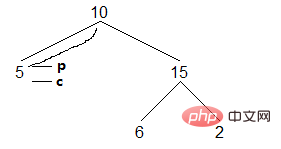
Result: []
(3) The left son of current node c is empty, access. After accessing, point c to the right son (i.e., the successor node):
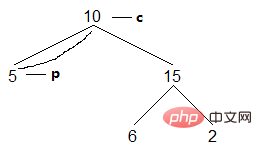
Result: [5]
(4) Continue to search for the left subtree The rightmost node, this time the termination condition is that the rightmost node is the current node. This shows that the left subtree of the current node has been traversed. After accessing the current node, restore the binary tree and point the current node to the successor node:
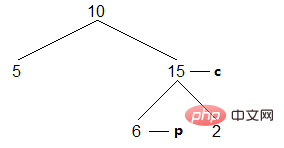
Result: [5,10 ]
(5) Repeat the above process until c points to the rightmost node of the entire binary tree:
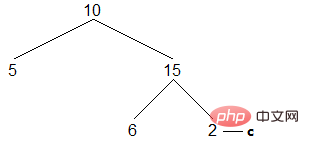
The left son is empty, access , c goes to the right son. The right son is empty and does not meet the judgment condition. The loop ends and the traversal is completed. The result is as follows:
[5,10,6,15,2]
This is the Morris method, the time complexity is O(n), and the space complexity is O(1). The code is as follows:
//Morris traversal,without a stack
class Solution3 {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> ret;
if(root==NULL)return ret;
TreeNode *curr=root;
TreeNode *pre;
while(curr)
{
if(curr->left==NULL)
{
ret.push_back(curr->val);
curr=curr->right;
}
else
{
pre=curr->left;
while(pre->right&&pre->right!=curr)
pre=pre->right;
if(pre->right==NULL)
{
pre->right=curr;
curr=curr->left;
}
else
{
ret.push_back(curr->val);
pre->right=NULL;
curr=curr->right;
}
}
}
return ret;
}
};Recommended tutorial: "C#"
The above is the detailed content of How is in-order traversal performed?. For more information, please follow other related articles on the PHP Chinese website!