What is the shortest path in graph applications in PHP data structure?-PHP Tutorial-php.cn

Application of graphs: shortest path

Do you feel like you still have more to learn about the minimum spanning tree in the previous article? I don’t know how well you have mastered it. Have you figured out the principles of Prim and Kruskal? If you can't write it during the interview, at least give a rough idea. Of course, if you are a student taking the postgraduate entrance examination, you need to deeply understand and remember the code of the entire algorithm.

What is the shortest path

What we are learning today is another classic problem in graph applications, that is, the shortest path problem. This problem is different from the minimum spanning tree. The requirement of the minimum spanning tree is to connect all the nodes and take the route with the smallest weight. The shortest path refers to the path with the smallest weight from a vertex to another vertex. This path is not necessarily included in the minimum spanning tree, so they are not much related.

What is the shortest path in graph applications in PHP data structure?

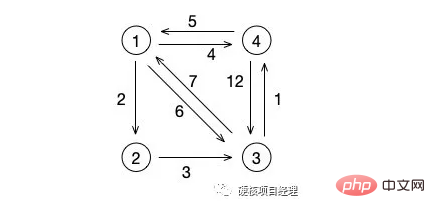
From this picture, our shortest path from node 1 to node 2 is 2, this is obvious. So what about from node 1 to node 3? Not the direct middle path with a weight of 6, but the path 1->2->3, which is the path with a total weight of 5.

Then let’s look at node 3. The shortest path to node 1 should be the path 3->4->1, which is the path with a weight of 6, not The middle line has a weight of 7.

Yes, this is the concept of the shortest path. In the shortest path, we usually solve the problem of one-way graph, but what about in real life? The most typical map-related applications are actually two-way graphs. However, this does not affect our learning. We can regard the nodes in this example diagram as city train stations. Even the train lines connecting node 1 and node 3 do not necessarily come and go at the same time. of. For example, the total running time of train Z2 from Changsha to Beijing is 14 hours and 42 minutes, while the return time of train Z1 is 14 hours and 10 minutes. So can we choose other trains? For example, there is a train that may only take 8 hours from Changsha to Shijiazhuang, and then only 2 hours from Shijiazhuang to Beijing. In this way, the total time we choose this route will only take 10 hours (of course , this is just an example. People will definitely choose the train at the starting station if it is not a high-speed rail.)

Multi-source shortest path Floyd algorithm

First, let’s talk about a multi-source shortest path algorithm. So what is multi-source?

In fact, this algorithm can find the shortest path from all nodes to all nodes. That's right, with this algorithm, no matter which node goes to which node, the shortest path between them is calculated at once. Is it magical? No, no, no, what’s even more amazing, and what will make you shout Oh! My God! in a moment, is its core code, which is only five lines! !

function Floyd($graphArr){
    $n = count($graphArr);
    
    for($k = 1;$k<=$n;$k++){ // 设 k 为经过的结点
        for($i = 1;$i<=$n;$i++){
            for($j = 1;$j<=$n;$j++){
                // 如果经过 k 结点 能使 i 到 j 的路径变短，那么将 i 到 j 之间的更新为通过 k 中转之后的结果 
                if($graphArr[$i][$j] > $graphArr[$i][$k] + $graphArr[$k][$j]){
                    $graphArr[$i][$j] = $graphArr[$i][$k] + $graphArr[$k][$j];
                }
            }
        }
    }
    for($i = 1;$i<=$n;$i++){
        for($j = 1;$j<=$n;$j++){
            echo $graphArr[$i][$j], &#39; &#39;;
        }
        echo PHP_EOL;
    }
}
// 请输入结点数：4 
// 请输入边数：8
// 请输入边，格式为 出 入 权：1 2 2
// 请输入边，格式为 出 入 权：1 3 6
// 请输入边，格式为 出 入 权：1 4 4 
// 请输入边，格式为 出 入 权：2 3 3
// 请输入边，格式为 出 入 权：3 1 7
// 请输入边，格式为 出 入 权：3 4 1
// 请输入边，格式为 出 入 权：4 1 5
// 请输入边，格式为 出 入 权：4 3 12
// 0 2 5 4 
// 9 0 3 4 
// 6 8 0 1 
// 5 7 10 0

Copy after login

We can verify the result first, which is the matrix output at the end of the comment. The shortest distances from node 1 to nodes 2, 3, and 4 are 2, 5, and 4. The shortest distances from node 3 to nodes 1, 2, and 4 are 6, 8, and 1. In other words, the adjacency matrix of the original graph becomes the matrix of the shortest path. Each row represents the shortest distance from each node to other nodes.

Okay, the result is okay, so what exactly is the code written? What is this k? Don't worry, let's look at it step by step.

Assuming that the distance between two points is not the shortest, then there must be another point as a medium for jumping. From point i, jump to this point first and then jump to point j. Such a path is closer than the direct i to j, we define this point as k point

But we don’t know which node to go to, and there may be more than one k, maybe we go from i to j has to go through many k. At this time, we start traversing from k, which is the first level of loop

Under the first level of loop, we perform our normal traversal loop of i and j, and obtain i directly The length to j, that is, [i][j]. At this time, due to the existence of the outermost k, we also know the length from k to j if i walks from k, which is the distance [i][k] [k][i]

Obviously, if the distance of [i][k] [k][i] is shorter than [i][j], update the value of [i][j] to [i][k] [k ][i]

After the internal i and j loops are completed, the traversal of the first node as a media jump is also completed. The weights between each node in the current matrix have been passed through the The shortest path after 1 node is used as the medium

However, this is not accurate. Maybe the path we may pass through i, k1, k2, j is the shortest, so the outer k The loop continues to traverse and the second node is used as the intermediary node

The loop continues until all nodes have visited the intermediate intermediary node once, and we obtain a matrix graph of the shortest path, that is We will take node 4 and node 3 to illustrate the results output in our test code above

. We define 4 as i and node 3 as j.

初始化时，[i][j] 为 12 ，这个没什么问题，单向图的那条带箭头的边的权值就是 12 。

然后当 k 为 1 时，也就是我们经过结点 1 来看路径有没有变短，这时 [i][k] 是 5 ，[k][j] 是 6 ，OK，路径变成 11 了，把 [i][j] 的值改成 11 。

同时，在 i 为 4 ，j 为 2 的情况下，他们两个的最短路径也在这次 k=1 的循环中被赋值为 7 。最开始 4 到 2 是没有直接的边的，现在在结点 1 的连接下，他们有了路径，也就是 [4][2] = [4][1] + [1][2] = 7 。

当 k 为 2 时，[i][j] 为 11 ，这时 [i][k] 就是上面说过的 [4][2] 。也就是 7 ，而 [k][j] 则是 3 ，路径又缩小了，[i][k] + [k][j] = 10 ，[i][j] 现在又变成了 10 。

循环继续，但已经没有比这条路径更小的值了，所以最后 [4][2] 的最短路径就是 10 。

看着晕吗？拿出笔来在纸上或者本子上自己画画，每一步的 k 都去画一下当前的最短路径矩阵变成什么样了。这样画一次之后，马上就知道这个 Floyd 算法的核心奥秘所在了。

不得不说，前人的智慧真的很伟大吧，不过说是前人，其实 Floyd 大佬在 1962 年才发表了这个算法，但这个算法的核心思想却是数学中的动态规划的思想。所以说，算法和数学是没法分家的，各位大佬哪个不是数学界的一把手呢。

单源最短路径 Dijkstra 算法

说完了多源最短路径，我们再讲一个鼎鼎大名的单源最短路径的算法。虽说上面的多源很牛X，但是它的时间复杂度也就是时间效率也确实是太差了，没看错的话三个 N 次的循环嵌套就是 O(N3)。如果数据稍微多一点的话基本就可以从 Oh!My God! 变成 Oh!FxxK! 了。而且大多数情况下，我们的需求都会是固定的求从某一点到另一点的最短路径问题，也就是单源最短路径问题。这时，就可以使用这种效率稍微好一点的算法来快速地解决了。

// origin 表示源点，也就是我们要看哪个结点到其它结点的最短路径
function Dijkstra($graphArr, $origin)
{
    $n = count($graphArr);
    $dis = []; // 记录最小值
    $book = []; // 记录结点是否访问过
    // 初始化源点到每个点的权值
    for ($i = 1; $i <= $n; $i++) {
        $dis[$i] = $graphArr[$origin][$i]; // 源点到其它点的默认权值
        $book[$i] = 0; // 所有结点都没访问过
    }
    $book[$origin] = 1; // 源点自身标记为已访问
    // 核心算法
    for ($i = 1; $i <= $n - 1; $i++) {
        $min = INFINITY;
        // 找到离目标结点最近的结点
        for ($j = 1; $j <= $n; $j++) {
            // 如果结点没有被访问过，并且当前结点的权值小于 min 值
            if ($book[$j] == 0 && $dis[$j] < $min) {
                $min = $dis[$j]; // min 修改为当前这个节点的路径值
                $u = $j; // 变量 u 变为当前这个结点
            }
            // 遍历完所有结点，u 就是最近的那个顶点
        }
        $book[$u] = 1; // 标记 u 为已访问
        for ($v = 1; $v <= $n; $v++) {
            // 如果 [u][v] 顶点小于无穷
            if ($graphArr[$u][$v] < INFINITY) {
                // 如果当前 dis[v] 中的权值大于 dis[u]+g[u][v]
                if ($dis[$v] > $dis[$u] + $graphArr[$u][$v]) {
                    // 将当前的 dis[v] 赋值为 dis[u]+g[u][v]
                    $dis[$v] = $dis[$u] + $graphArr[$u][$v];
                }
            }
        }
        // 最近的结点完成，继续下一个最近的结点
    }
    for ($i = 1; $i <= $n; $i++) {
        echo $dis[$i], PHP_EOL;
    }
}
// 请输入结点数：4 
// 请输入边数：8
// 请输入边，格式为 出 入 权：1 2 2
// 请输入边，格式为 出 入 权：1 3 6
// 请输入边，格式为 出 入 权：1 4 4 
// 请输入边，格式为 出 入 权：2 3 3
// 请输入边，格式为 出 入 权：3 1 7
// 请输入边，格式为 出 入 权：3 4 1
// 请输入边，格式为 出 入 权：4 1 5
// 请输入边，格式为 出 入 权：4 3 12
// 测试第四个结点到其它结点的最短路径
Dijkstra($graphArr, 4);
// 5
// 7
// 10
// 0

Copy after login

代码一下增加了不少吧，不过仔细看一下核心的算法部分，这次只是两层循环的嵌套了，时间复杂度一下子就降到了 O(N2) ，这一下就比 Floyd 算法提升了很多。当然，它的场景也是有限的，那就是只能一个结点一个结点的计算。

好了，我们还是来看一下 Dijkstra 到底在干嘛吧。我们依然是使用上面那个简单的图，并且还是研究结点 4 到其它结点的算法执行情况。

首先，我们初始化结点 4 到其他所有结点的默认值，这时结点 4 到结点 2 是没有直接路径的，所以是无穷大，而到结点 1 是 5，到结点 3 是 12 。

然后将结点 4 标记为已访问，也就是 book[4] = 1

进入核心算法，从头开始遍历结点，这里是标记为 i 下标，因为这里是单源的最短路径，所以我们不需要再看自己到自己的最短路径了，只需要 n-1 次循环就可以了

开始 j 层的循环，先判断当前的结点是否已经被标记过，没有被标记过的话再看它的值是否是最小的，最后循环完成后获得一个从结点 4 出发的权值最小的路径，并将这条路径到达的结点下标记为 u ，标记 u 下标的这个结点为已访问结点

进入 v 循环，判断图中 u 到 v 的结点是否是无穷，如果不是的话再判断 u 到 v 的结点加上原来的 dis[u] 的权值是否小于 dis[v] 中记录的权值，如果比这个小的话，更新 dis[v] 为 u 到 v 的结点加上原来的 dis[u] 的权值

循环重复地进行比较完成算法

对于结点 4 来说，dis 经历了如下的变化：

首先，默认情况下 dis = [5, 9999999, 12, 0]

第一次循环后，结点1 完成查找，并在 v 的循环中发现了可以从结点1 到结点2 和结点3 而且比原来的值都要小，于是 dis = [5, 7, 11, 0]

第二次循环后，结点2 完成查找，这次循环发现从结点2 到结点3 的距离更短，于是 dis = [5, 7, 10, 0]

第三次循环后，结点3 完成查找，没有发现更短的路径，dis = [5, 7, 10, 0]

看明白了吗？不明白的话自己试试吧，不管是断点还是在中间输出一下 dis 和 book ，都能够帮助我们更好地理解这个算法的每一步是如何执行的。从代码中就可以看出来，这个 Dijkstra 算法的时间复杂度是 O(N2) ，这可比 Floyd 快了不少了吧。

总结

关于图的两种最典型的应用及算法就到这里结束了。当然，图的内容可远不止这些，比较典型的还是进度网络图等的算法，特别是做一些项目管理类的系统时会非常有用。当然，更高深的内容就要去研究《图论》了。这个可就远超我的水平了，希望有更多数学相关基础的同学能够继续深入研究。而我嘛，先去恶补下数学吧！！

测试代码：
https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/5.图/source/5.5图的应用：最短路径.php

Copy after login