A brief discussion on why floating point operations produce errors

This article takes Python as an example to talk about why floating point operations produce errors? Please introduce the circumstances under which errors may occur? and how to solve it? Hope it helps you.

[Related recommendations: Python3 video tutorial ]

Everyone will encounter the so-called floating point error when writing code. If If you haven't stepped into the pit of floating point error, I can only say that you are too lucky.

Take the Python picture below as an example, 0.1 0.2 is not equal to 0.3, nor is 8.7 / 10 equal to 0.87, but 0.869999…, it’s so strange

But this is definitely not a hellish bug, nor is it a problem with Python’s design, but Floating point numbers are inevitable results when performing operations, so they are the same even in JavaScript or other languages:

How does a computer store an integer ( Integer)

Before talking about why floating point errors exist, let’s first talk about how computers use 0 and 1 to represent an integer. Everyone should know binary: For example, 101 represents $2^2 2^0$, which is 5, and 1010 represents $2^3 2^1$, which is 10.

If it is an unsigned 32-bit integer, it means that it has 32 positions where 0 or 1 can be placed, so the minimum value is 0000...0000 is 0, and the maximum value 1111...1111 represents $2^{31} 2^{30} ... 2^1 2^0$ which is 4294967295

From the perspective of permutation and combination, because each bit can be 0 or 1, the value of the entire variable has $2^{32}$ possibilities, so it can accurately express 0 to $2^ Any value between {23} - 1$ without any error.

Floating Point

Although there are many integers between 0 and $2^{23} - 1$, the number is ultimately Limited is just as many as $2^{32}$; but floating point numbers are different. We can think of it this way: there are only ten integers in the range from 1 to 10, but there are infinitely many A floating point number, such as 5.1, 5.11, 5.111, etc., the list is endless.

But because there are only 2³² possibilities in the 32-bit space, in order to stuff all floating-point numbers into this 32-bit space, many CPU manufacturers have invented various floating-point number representation methods, but It would be troublesome if the format of each CPU was different, so in the end, IEEE 754 published by IEEE was used as the general floating point calculation standard. Today's CPUs are also designed according to this standard.

IEEE 754

IEEE 754 defines many things, including single precision (32 bit), double precision (64 bit) and special values ​​(infinity, NaN ), etc.

Standardization

For a floating point number of 8.5, if you want to change it to IEEE 754 format, you must first Do some normalization: split 8.5 into 8 0.5, which is $2^3 (\cfrac{1}{2})^1$, then write it in binary to become 1000.1, and finally write it as $1.0001 \ times 2^3$, which is very similar to decimal scientific notation.

Single-precision floating-point number

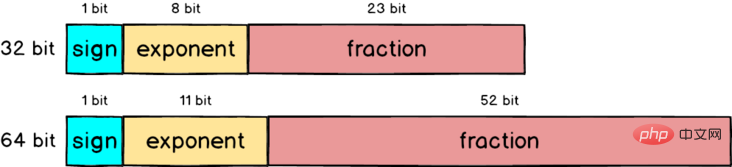
In IEEE 754, a 32-bit floating-point number is split into three parts, namely the sign ), exponent and fraction, the total is 32 bits

• Sign: the leftmost 1 bit Represents the positive and negative sign. If it is a positive number, the sign is 0, otherwise it is 1
• exponent: the 8 bits in the middle represent the power after normalization, using the exponent The format of the true value 127, that is, 3 plus 127 is equal to 130
• mantissa (fraction): the 23 bits on the rightmost place is the decimal part, starting with 1.0001 In short, 0001
is removed after

1.

. So if 8.5 is expressed in 32 bit format, it should be like this:

Under what circumstances will errors occur?

The example of 8.5 mentioned above can be expressed as $2^3 (\cfrac{1}{2})^1$ because 8 and 0.5 are both powers of 2. number, so there will be no accuracy issues at all.

But if it is 8.9, there is no way to add powers of 2, so it will be forced to be expressed as $1.0001110011... \times 2^3$, and there will also be an error of about $0.0000003$. If the result is If you are curious, you can go to the IEEE-754 Floating Point Converter website to play around.

Double-precision floating-point number

#The single-precision floating-point number mentioned earlier is represented by only 32 bits. In order to make the error smaller, IEEE 754 also defines how to use 64 bits to represent floating point numbers. Compared with 32 bits, the fraction part is expanded more than twice, from 23 bits to 52 bits, so the accuracy will naturally be improved a lot.

Take the 8.9 just now as an example. Although it can be more accurate if expressed in 64 bits, 8.9 cannot be completely written as the sum of powers of 2. When it comes to decimals There will still be an error in the lower 16 bits, but it is much smaller than the single-precision error of 0.0000003

Similar situations are also like 1.0# in Python ## is equal to 0.999...999, 123 is also equal to 122.999...999, because the gap between them is so small They cannot be placed in fraction, so from the binary format, every binary bit is the same.

Solution

Since the error of floating point numbers is unavoidable, we have to live with it. The following are two A more common processing method:

Set the maximum allowable error ε (epsilon)

In some languages, the so-called epsilon is provided. It is used to let you judge whether it is within the allowed range of floating point error. In Python, the value of epsilon is approximately $2.2e^{-16}$

, so you You can rewrite

0.1 0.2 == 0.3 as 0.1 0.2 — 0.3 , so as to avoid floating point errors from causing trouble during the operation, and correctly compare 0.1 plus 0.2 Is it equal to 0.3?

Of course, if the system does not provide it, you can also define an epsilon by yourself, setting it around 2 to the power of -15

Completely use decimal system for calculation

The reason why there are floating point errors is because it is impossible to stuff all the decimal parts into the mantissa during the process of converting decimal to binary. Since there may be errors in the conversion, then simply No need to convert, just use decimal to do the calculations.

There is a module called decimal in Python, and there is a similar package in JavaScript. It can help you perform calculations in decimal, just like you can calculate 0.1 0.2 with pen and paper without any error or error.

Although using decimal for calculation can completely avoid errors in floating point numbers, because Decimal's decimal calculation is simulated, binary is still used in the lowest-level CPU circuit. The operation will be much slower than the native floating point operation, so it is not recommended to use Decimal for all floating point operations.

For more programming-related knowledge, please visit:

Introduction to Programming! !

The above is the detailed content of A brief discussion on why floating point operations produce errors. For more information, please follow other related articles on the PHP Chinese website!