
I am currently working on a small requirement. Each order will determine the maximum red envelope that the user can use based on the amount. If the user chooses to use red envelopes, we need to help the user select the optimal red envelope combination from the list of red envelopes they have. The combined red envelope value is required to be closest to or equal to the maximum value of the red envelope that can be used. After thinking about it for a while, isn't this the "0-1 knapsack problem"? I can finally put the "dynamic programming" algorithm I have learned before into practice!
Dynamic programming (Dynamic programming abbreviation: DP) is a method in mathematics, management science, computer science, economics and biology. A method used in informatics to solve complex problems by decomposing the original problem into relatively simple sub-problems.
Dynamic programming is often suitable for problems with overlapping subproblems and optimal substructure properties. Dynamic programming methods often take much less time than naive solutions.
Dynamic programming is generally used to solve the problem of finding the optimal solution. In the process of solving the problem, multiple decisions are required, and each decision produces a set of states, and then the next decision is continued from the optimal decision to finally find the optimal result.
In addition, dynamic programming also has 3 characteristics, as follows:
If the optimal solution of the problem contains sub The solution to the problem is also optimal, and we say that the problem has optimal substructure properties (that is, it satisfies the optimization principle). Therefore, we can deduce the optimal solution of the problem through the optimal solution of the sub-problem. It can also be understood that the state of the later stage can be deduced from the state of the previous stage.
That is, once the solution of the sub-problem is determined, it will no longer change and will not be affected by the solution of the larger problem that includes it. Decision-making impact.
It can be simply understood that when deriving the state of a later stage, we only need to care about the state of the previous stage, and do not need to care about how this state is derived step by step. The second meaning is that once the status of a certain stage is determined, it will not be affected by decisions in subsequent stages.
The overlapping property of sub-problems means that when a recursive algorithm is used to solve the problem from top to bottom, the sub-problems generated each time are not the same. There are always new problems, and some sub-problems will be recalculated multiple times
The above theory is relatively abstract and just like nonsense. Come on. Consider the classic knapsack problem.
Suppose there are 5 items and their weights are 2, 2, 5, 11, 4. Now there is a backpack, and the maximum weight it can bear is 10, please choose the appropriate items to put into the backpack. What is the maximum weight of the items that can be combined?
Different combinations of items will have many different states. We can use f(i, w) to represent a state, where i = index represents the item number, w = weight represents the current total weight.
The entire problem needs to be solved through 『n』 stages. Each stage requires a decision as to whether to put an item into the backpack. There are only two outcomes of the decision: 『Put it in』 or 『Do not put it in』. After deciding on an item, the weight of the item in the backpack will have many different states. We need to merge the duplicate states of each layer, and then only leave the different states. Then the status results of the next layer are derived based on the status results of the previous layer. In the end, the optimal combination solution can be found after all items have been decided.
The weight of the 0th item (actually the first item, let’s start subscripting from 0 as usual) is 2, and then we start to decide whether to put it in the backpack, and there are only 2 results. If you put it in the backpack, the weight of the backpack at this time is 2. If you don't put it in the backpack, the weight of the backpack is 0. Record it as $status[0][0] = true; and $status [0][2] = true; Same as f(i, w) above, the former digit represents the item and the latter digit represents the weight.
The weight of the first item is still 2, and then we start to make a decision about it. There are only two choices for decision-making: put it in the backpack or not put it in the backpack, but its status combinations are more, because it is based on the previous one. The backpack status is used to determine the current status. After completing the decision on the first item, there will be 3 states (actually 4 states, but if there is 1 duplicate, it will not be counted. It will still be counted as 3 different states).
If the decision is made to put the current item into the backpack and the 0th item is not put into the backpack, the status at this time is $status[1][2 0] = true; => $status[1][2 ] = true;
If the decision is made to put the current item into the backpack, and the 0th item is also put into the backpack, the status at this time is$status[1][2 2] = true; => $status[1][4] = true;
If the current item is decided not to be put into the backpack, and the 0th item is not put into the backpack, the status at this time is$status[1 ][0 0] = true; => $status[1][0] = true;
If the decision is made not to put the current item into the backpack, but the 0th item is put into the backpack, the status at this time is$status[1][0 2] = true; => $status[1][2] = true;
where$status[1][2 ] is repeated and will produce 3 results.
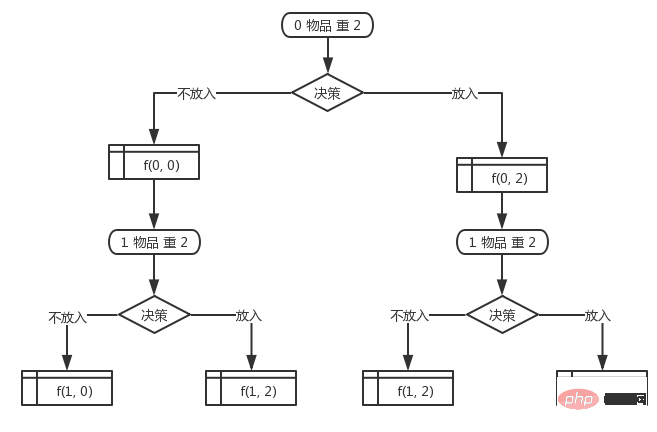
The following items are also deduced in the same way. Until all items have been decided, the entire status array has been found, and then only the last layer needs to be found. A value of true that is closest to the maximum value (10 in the example above) is the maximum value the backpack can hold. Then you can push forward from the end to find out the corresponding item subscripts, that is, which combination of items is the optimal solution combination.
The derivation process is as follows:



In fact, the above derivation process is dynamic programming Problem-solving ideas. Break the problem into stages, with each stage corresponding to a strategy. Then record the status of each stage (be careful to remove duplicates), and then deduce all possible states of the next stage through the possibilities of the current state, and deduce it dynamically.
PHP implementation pseudo code:
function dynamicKnapsack($arr, $n, $max){
// 初始化二维数组
$status = [];
for ($i = 0; $i = 0; $j--) {
if ($status[$n - 1][$j] == true) {
break;
}
}
for ($i = $n - 1; $i >= 1; $i--) { // 外层遍历行
if ($j - $arr[$i] >= 0 && $status[$i - 1][$j - $arr[$i]] == 1) {
var_dump('buy this product: '.$arr[$i]);
$best[] = $i;
$j = $j - $arr[$i];
}
}
if ($j != 0) {
var_dump('buy first product:'.$arr[0]);
$best[] = 0;
}
return $best;}// 测试数据$arr = [
2, 2, 5, 11, 4,];$n = 5;$max = 10;$best = dynamicKnapsack($arr, $n, $max);var_dump($best);If the result is 11, the result is a combination of 4, 5, 2, You may have questions, isn't there another result of 11? It just happens to be enough, isn't it? I think this should depend on actual needs. For example, my requirement this time is to sort the red envelopes by expiration time, and use the ones that are about to expire first. Then when assembling the data, I force the red envelopes that are about to expire to the end of the array in the order of expiration time to form an array. Then the last 4 It’s the red envelope that’s about to expire. I want to consume this red envelope first. If I use 4, I can’t use 11. I can only continue to look for it at the front. That’s it!
What is the time complexity of this code? The most time-consuming part is the nested 2-layer loop in the middle, and the total time complexity isO(n*max), where n represents the number of items and max represents the maximum load-bearing capacity.
The space complexity is the array space applied for at the beginningO(n*max 1) Plus the accumulation of calculation results may occurO(n*2*max) situation, the space consumption is still very high.
Generally speaking, this is an idea of exchanging space for time. In addition, if you use j to traverse from small to large in the nested loop of the intermediate decision-making, there will be a problem of repeated calculations in the for loop.
Recommended study: "PHP Video Tutorial"
The above is the detailed content of Detailed explanation of how PHP uses dynamic programming to achieve the optimal red envelope combination. For more information, please follow other related articles on the PHP Chinese website!