This article will introduce to you how to implement Monte Carlo tree search using Node.js, and use the Monte Carlo tree search (MCTS) algorithm to play a game with given rules. Let’s do it together. Let's see!
This article assumes that the reader has a certain knowledge of computer science, especially the working principle of tree structure in data structures, and also needs to have JavaScript Intermediate knowledge of (ES6). Recommended learning: "nodejs Tutorial"】
The goal of this article is simple:
Implement the Monte Carlo Tree Search (MCTS) algorithm to play a game with given rules .
This entire process will be instructive and practical, and ignore the performance optimization part. I'll give a brief explanation of the linked code snippet in the hope that you'll follow along and take some time to understand the complex parts of the code.
let's start!
In game.js file:
/** 代表游戏棋盘的类。 */
class Game {
/** 生成并返回游戏的初始状态。 */
start() {
// TODO
return state
}
/** 返回当前玩家在给定状态下的合法移动。 */
legalPlays(state) {
// TODO
return plays
}
/** 将给定的状态提前并返回。 */
nextState(state, move) {
// TODO
return newState
}
/** 返回游戏的胜利者。 */
winner(state) {
// TODO
return winner
}
}
module.exports = GameIn monte-carlo.js In the file:
/** 表示蒙特卡洛树搜索的类。 */
class MonteCarlo {
/** 从给定的状态中，反复运行 MCTS 来建立统计数据。 */
runSearch(state, timeout) {
// TODO
}
/** 从现有的统计数据中获取最佳的移动。 */
bestPlay(state) {
// TODO
// return play
}
}
module.exports = MonteCarlo In the index.js file:
const Game = require('./game.js')
const MonteCarlo = require('./monte-carlo.js')
let game = new Game()
let mcts = new MonteCarlo(game)
let state = game.start()
let winner = game.winner(state)
// 从初始状态开始轮流进行游戏，直到有玩家胜利为止
while (winner === null) {
mcts.runSearch(state, 1)
let play = mcts.bestPlay(state)
state = game.nextState(state, play)
winner = game.winner(state)
}
console.log(winner)Take some time to sort out the code first. Scaffold a subreddit in your mind and try to understand it. This is a mental checkpoint. Make sure you understand how it fits together. If you feel you can't understand it, please leave a message and let me see what I can do for you.
In the context of developing a MCTS game agent, we can think of our real program as the code that implements the MCTS framework, as well as That's the code in the monte-carlo.js file. The game-specific code in the game.js file is interchangeable and plug-and-play, and is our interface to the MCTS framework. We basically wanted to be the brains behind MCTS, which should really run on any game. After all, we're interested in general gameplay.
However, in order to test our MCTS framework, we need to select a specific game and run our framework using that game. We would like to see the MCTS framework make decisions at every step that make sense for the game we choose.
How about making a game of tic-tac-toe (Tic-Tac-Toe)? It is used in almost all introductory game tutorials, and it also has some very satisfying features:
But, tic-tac-toe is really boring, isn't it? Plus, you presumably already know the best strategy for Tic-Tac-Toe, which loses some of its appeal. With so many games to choose from, how about we pick another one: Connect Four? In addition to perhaps enjoying lower popularity than Tic-Tac-Toe, it not only has the properties listed above, but may also make it less easy for players to build a mental model of the four-bang state space.
But before we continue, we need to explain something. If you're confident, you can implement any game you want yourself, as long as it adheres to the given game API. Just don't complain when you mess up and it doesn't work. Remember, games like chess and Go are too complex for even MCTS to solve (effectively) on their own; Google solved this in
AlphaGoby adding efficient machine learning strategies to MCTS question. If you want to play your own game, you can skip the next two parts.
Implementing the four-piece chess game to game-c4.js, Rename the class to Game_C4. At the same time, create two new classes: State_C4 in state-c4.js to represent the game state, Play_C4 in play-c4.js indicates state transition. Although this is not the main content of this article, how would you build it yourself?
State_C4 中表示一个游戏状态呢？Play_C4 中，你将如何表示一个状态转换（例如一个动作）呢？State_C4、Play_C4 和四子棋游戏规则 —— 用冰冷的代码放在 Game_C4 中吗？注意，我们需要通过骨架文件 game-c4.js 中定义的高级 API 方法所要求的形式实现四子棋游戏。
你可以独立思考完成或者直接使用我完成的 play-c4.js、state-c4.js 和 game-c4.js 文件。
这是一个工作量很大的活，不是吗？至少对我来说是这样的。这段代码需要一些 JavaScript 知识，但应该还是很容易读懂的。最重要的工作在 Game_C4.winner() 中 —— 它用于在四个独立的棋盘中建立积分系统，而所有的棋盘都在 checkBoards 里面。每个棋盘都有一个可能的获胜方向（水平、垂直、左对角线或右对角线）。我们需要确保棋盘的三个面比实际棋盘大，方便为算法提供零填充。
我相信还有更好的方法。Game.winner() 的运行时性能并不是很好，具体来说，在大 O 表示法中，它是 O(rows * cols)，所以性能并不是很好。通过在状态对象中存储 checkBoards，并且只更新 checkBoards 中最后改变状态的单元格（也会包含在状态对象中），可以大幅改善运行时性能，也许你以后可以尝试这个优化方法。
此时，我们将通过模拟 1000 次四子棋游戏来测试 Game_C4。点击获取 test-game-c4.js 文件。
在终端上运行 node test-game-c4.js。在一个相对现代的处理器和最新版本的 Node.js 上，运行 1000 次迭代应该会在一秒钟内完成：
$ node test-game-c4.js [ [ 0, 0, 0, 0, 0, 0, 2 ], [ 0, 2, 0, 0, 0, 0, 2 ], [ 0, 1, 0, 1, 2, 1, 2 ], [ 0, 2, 1, 2, 2, 1, 2 ], [ 0, 1, 1, 2, 1, 2, 1 ], [ 0, 1, 2, 1, 1, 2, 1 ] ] 0.549
二号棋手在内部用 -1 表示，这是为了方便 game-c4.js 的计算。用 2 代替 -1 的那段代码只是为了对齐棋盘输出结果。为了简便起见，程序只输出了一块棋盘，但它确实玩了另外的 999 次四子棋游戏。在单个棋盘输出之后，它应该输出一号棋手在所有 1000 盘棋中获胜的分数 —— 预计数值在 55% 左右，因为第一个棋手有先发优势。
我们已经实现一个带有 API 方法并且可以运行的游戏，这些 API 方法可以与 State 对象表示的游戏状态协同运行。我们现在的状况如何？
目标：实现蒙特卡洛树搜索（MCTS）算法来玩一个给定规则的游戏。
当然，我们还没有达到目的。刚才我们完成了一件非常重要的事情：让它设立一个切实的目标，并组成测试我们实现 MCTS 的核心模块。现在，我们进入正题。
在这里，我将按照 MCTS 详解中类似的组织方式，我也会在一些地方用自己的话来阐明某些观点。
为了存储从这些模拟中获得的统计信息，MCTS 从头开始建立了自己的搜索树。
现在请你回顾树结构知识。MCTS 是一个树结构搜索，因此我们需要使用树节点。我们将在 monte-carlo-node.js 的 MonteCarloNode 类中实现这些节点。然后，我们将在 MonteCarlo 中使用它来构建搜索树。
/** 代表搜索树中一个节点的类。 */
class MonteCarloNode {
constructor(parent, play, state, unexpandedPlays) {
this.play = play
this.state = state
// 蒙特卡洛的内容
this.n_plays = 0
this.n_wins = 0
// 树结构的内容
this.parent = parent
this.children = new Map()
for (let play of unexpandedPlays) {
this.children.set(play.hash(), { play: play, node: null })
}
}
...先再确认一下是否能够理解这些：
parent 是 MonteCarloNode 父节点。play 是指从父节点到这个节点所做的 Play。state 是指与该节点相关联的游戏 State。unexpandedPlays 是 Plays 的一个合法数组，可以从这个节点进行。this.children 是由 unexpandedPlays 创建的，是 Plays 指向子节点 MonteCarloNodes 的一个 Map 对象（不完全是，见下文）。MonteCarloNode.children 是一个从游戏哈希到对象的映射，包含游戏对象和相关的子节点。我们在这里包含了游戏对象，以便从它们的哈希中恢复游戏对象。
重要的是，Play 和 State 应该提供 hash() 方法。我们将在一些地方使用这些哈希作为 JavaScript 的 Map 对象，比如在 MonteCarloNode.children 中。
请注意，两个 State 对象应该被 State.hash() 认为是不同的 —— 即使它们有相同的棋盘状态 —— 如果每个对象通过不同的下棋顺序达到相同的棋盘状态。考虑到这一点，我们可以简单地让 State.hash() 返回一个字符串化的 Play 对象的有序数组，代表为达到该状态而下的棋。如果你获取了我的 state-c4.js，这个已经完成了。
现在我们将为 MonteCarloNode 添加成员方法。
...
/** 获取对应于给定游戏的 MonteCarloNode。 */
childNode(play) {
// TODO
// 返回 MonteCarloNode
}
/** 展开指定的 child play，并返回新的 child node。*/
expand(play, childState, unexpandedPlays) {
// TODO
// 返回 MonteCarloNode
}
/** 从这个节点 node 获取所有合法的 play。*/
allPlays() {
// TODO
// 返回 Play[]
}
/** 从这个节点 node 获取所有未展开的合法 play。 */
unexpandedPlays() {
// TODO
// 返回 Play[]
}
/** 该节点是否完全展开。 */
isFullyExpanded() {
// TODO
// 返回 bool
}
/** 该节点 node 在游戏树中是否为终端，
不包括因获胜而终止游戏。 */
isLeaf() {
// TODO
// 返回 bool
}
/** 获取该节点 node 的 UCB1 值。 */
getUCB1(biasParam) {
// TODO
// 返回 number
}
}
module.exports = MonteCarloNode方法可真多!
特别是，MonteCarloNode.expand() 将 MonteCarloNode.children 中未展开的空节点替换为实节点。这个方法将是四阶段的 MCTS 算法中阶段二：扩展的一部分，其他方法自行理解。
通常你可以自己实现这些，也可以获取完成的 monte-carlo-node.js。即使你自己做，我也建议在继续之前对照我完成的程序进行检查，以确保正常运行。
如果你刚获取到我完成的程序，请快速浏览一下源代码，就当是另一个心理检查点，重新梳理你的整体理解。这些都是简短的方法，你会在短时间内看懂它们。
尤其是 MonteCarloNode.getUCB1() 几乎是将上面的公式直接翻译成代码。这整个公式在上一篇文章中有详细的解释，再去看一下吧，这并不难理解，也是值得看的。
目前的版本是 monte-carlo-v1.js，只是一个骨架文件。该类的第一个更新是增加 MonteCarloNode，并创建一个构造函数。
const MonteCarloNode = require('./monte-carlo-node.js')
/** 表示蒙特卡洛搜索树的类。 */
class MonteCarlo {
constructor(game, UCB1ExploreParam = 2) {
this.game = game
this.UCB1ExploreParam = UCB1ExploreParam
this.nodes = new Map() // map: State.hash() => MonteCarloNode
}
...MonteCarlo.nodes 允许我们获取任何给定状态的节点，这将是有用的。至于其他的成员变量，将它们与 MonteCarlo 联系起来就很有意义了。
...
/** 如果给定的状态不存在，就创建空节点。 */
makeNode(state) {
if (!this.nodes.has(state.hash())) {
let unexpandedPlays = this.game.legalPlays(state).slice()
let node = new MonteCarloNode(null, null, state, unexpandedPlays)
this.nodes.set(state.hash(), node)
}
}
...以上代码让我们可以创建根节点，还可以创建任意节点，这可能很有用。
...
/** 从给定的状态，反复运行 MCTS 来建立统计数据。 */
runSearch(state, timeout = 3) {
this.makeNode(state)
let end = Date.now() + timeout * 1000
while (Date.now() < end) {
let node = this.select(state)
let winner = this.game.winner(node.state)
if (node.isLeaf() === false && winner === null) {
node = this.expand(node)
winner = this.simulate(node)
}
this.backpropagate(node, winner)
}
}
...最后，我们来到了算法的核心部分。引用第一篇文章的内容，以下是过程描述：
在第 (1) 阶段，利用现有的信息反复选择连续的子节点，直至搜索树的末端。
接下来，在第 (2) 阶段，通过增加一个节点来扩展搜索树。
然后，在第 (3) 阶段，模拟运行到最后，决定胜负。
最后，在第 (4) 阶段，所选路径中的所有节点都会用模拟游戏中获得的新信息进行更新。
这四个阶段的算法反复运行，直至收集到足够的信息，产生一个好的移动结果。
...
/** 从现有的统计数据中获得最佳的移动。 */
bestPlay(state) {
// TODO
// 返回 play
}
/** 第一阶段：选择。选择直到不完全展开或叶节点。 */
select(state) {
// TODO
// 返回 node
}
/** 第二阶段：扩展。随机展开一个未展开的子节点。 */
expand(node) {
// TODO
// 返回 childNode
}
/** 第三阶段：模拟。游戏到终止状态，返回获胜者。 */
simulate(node) {
// TODO
// 返回 winner
}
/** 第四阶段：反向传播。更新之前的统计数据。 */
backpropagate(node, winner) {
// TODO
}
}接下来讲解四个阶段具体的实现方法，我们现在的版本是 monte-carlo-v2.js。
从搜索树的根节点开始，我们通过反复选择一个合法移动，前进到相应的子节点来向下移动。如果一个节点中的一个、几个或全部合法移动在搜索树中没有对应的节点，我们就停止选择。
...
/** 第一阶段：选择。选择直到不完全展开或叶节点。 */
select(state) {
let node = this.nodes.get(state.hash())
while(node.isFullyExpanded() && !node.isLeaf()) {
let plays = node.allPlays()
let bestPlay
let bestUCB1 = -Infinity
for (let play of plays) {
let childUCB1 = node.childNode(play)
.getUCB1(this.UCB1ExploreParam)
if (childUCB1 > bestUCB1) {
bestPlay = play
bestUCB1 = childUCB1
}
}
node = node.childNode(bestPlay)
}
return node
}
...该函数通过查询每个子节点的 UCB1 值，使用现有的 UCB1 统计。选择 UCB1 值最高的子节点，然后对所选子节点的子节点重复这个过程，以此类推。
当循环终止时，保证所选节点至少有一个未展开的子节点，除非该节点是叶子节点。这种情况是由调用函数 MonteCarlo.runSearch() 处理的，所以我们在这里不必担心。
停止选择后，搜索树中至少会有一个未展开的移动。现在，我们随机选择其中的一个，然后我们创建该移动对应的子节点（图中加粗）。我们将这个节点作为子节点添加到选择阶段最后选择的节点上，扩展搜索树。节点中的统计信息初始化为
0次模拟中的0次胜利。
...
/** 第二阶段：扩展。随机展开一个未展开的子节点。 */
expand(node) {
let plays = node.unexpandedPlays()
let index = Math.floor(Math.random() * plays.length)
let play = plays[index]
let childState = this.game.nextState(node.state, play)
let childUnexpandedPlays = this.game.legalPlays(childState)
let childNode = node.expand(play, childState, childUnexpandedPlays)
this.nodes.set(childState.hash(), childNode)
return childNode
}
...再来看一下 MonteCarlo.runSearch()。扩展是在检查 if (node.isLeaf() === false && winner === null) 时完成的。很明显，如果在游戏树中没有可能的子节点 —— 例如，当棋盘满了的时候，是不可能进行扩展的。如果有赢家的话，我们也不想扩展 —— 这就像说当你的对手赢了的时候你应该停止玩游戏一样明显。
那么如果是叶子节点，会发生什么呢？我们只需用在该节点中获胜的人进行反向传播 —— 无论是玩家 1，玩家 -1，甚至是 0（平局）。同样，如果在任何节点上有一个非空的赢家，我们只需跳过扩展和模拟，并立即与该赢家（1 或 -1 或 0）进行反向传播。
反向传播 0 赢家是什么意思？用 MCTS 真的可以吗？真的可以用，后面再细讲。
从扩张阶段新建立的节点开始，随机选择棋步，反复推进对局状态。这样重复进行，直到对局结束，出现赢家。在此阶段不创建新节点。
...
/** 第三阶段：模拟。游戏到终止状态，返回获胜者。 */
simulate(node) {
let state = node.state
let winner = this.game.winner(state)
while (winner === null) {
let plays = this.game.legalPlays(state)
let play = plays[Math.floor(Math.random() * plays.length)]
state = this.game.nextState(state, play)
winner = this.game.winner(state)
}
return winner
}
...因为这里没有保存任何东西，所以这主要涉及到 Game，而 MonteCarloNode 的内容不多。
再看一下 MonteCarlo.runSearch()，模拟是在与扩展一样的检查 if (node.isLeaf() === false && winner === null) 时完成的。原因是：如果这两个条件之一成立，那么最后的赢家就是当前节点的赢家，我们只是用这个赢家进行反向传播。
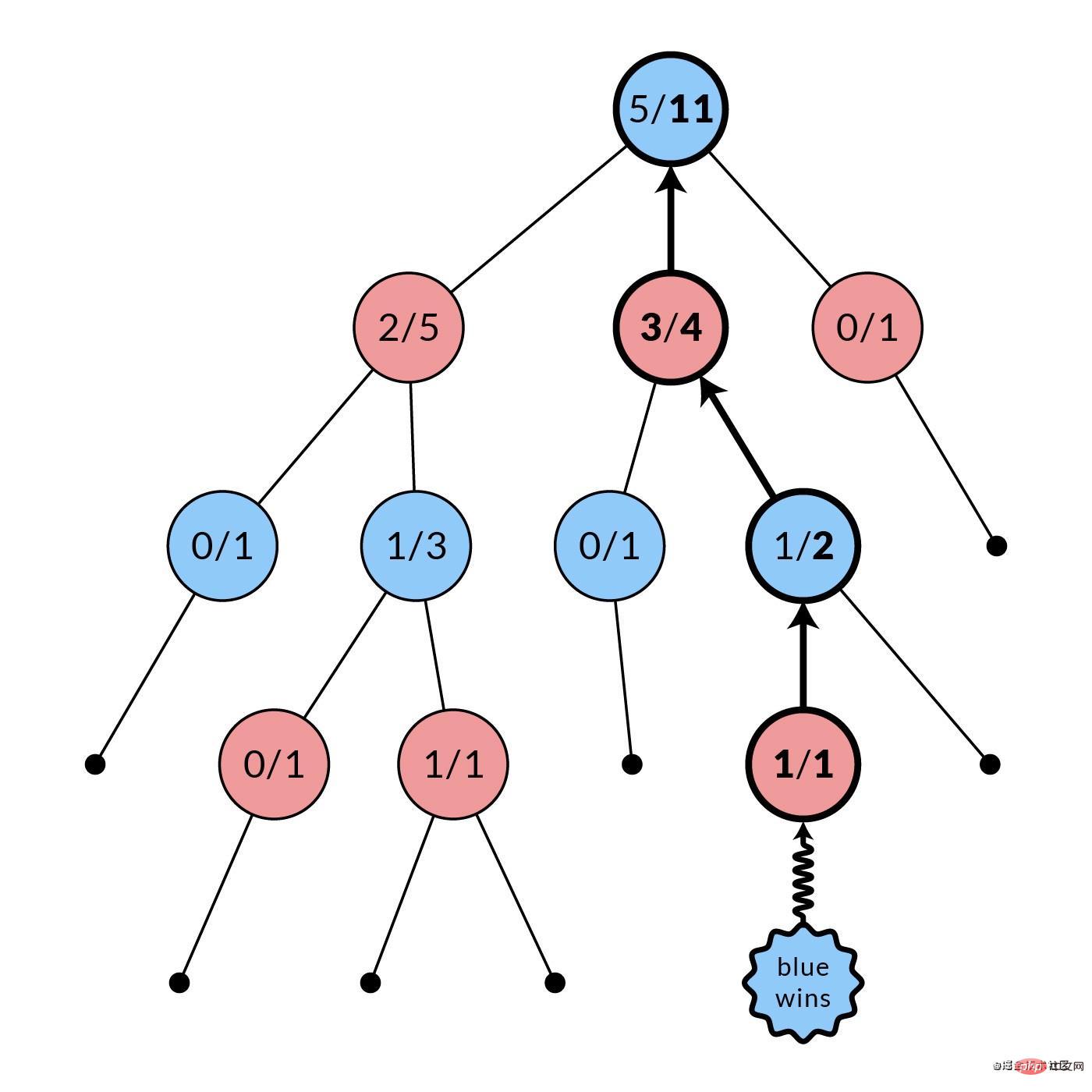
模拟阶段结束后，所有被访问的节点（图中粗体）的统计数据都会被更新。每个被访问的节点的模拟次数都会递增。根据哪个玩家获胜，其获胜次数也可能递增。在图中，蓝节点赢了，所以每个被访问的红节点的胜利数都会递增。这种反转是由于每个节点的统计数据是用于其父节点的选择，而不是它自己的。
...
/** 第四阶段：反向传播。更新之前的统计数据。 */
backpropagate(node, winner) {
while (node !== null) {
node.n_plays += 1
// 父节点的选择
if (node.state.isPlayer(-winner)) {
node.n_wins += 1
}
node = node.parent
}
}
}
module.exports = MonteCarlo这是影响下一次迭代搜索中选择阶段的部分。请注意，这假设是一个两人游戏，允许在 node.state.isPlayer(-winner) 中进行反转。你也许可以把这个函数泛化为 n 人游戏，做成 node.parent.state.isPlayer(winner) 之类的。
想一想，反向传播 0 赢家是什么意思？这相当于一盘平局，每个访问节点的 n_plays 统计数据都会增加，而玩家 1 和玩家 -1 的 n_wins 统计数据都不会增加。这种更新的行为就像两败俱伤的游戏，将选择推向其他游戏。最后，以平局结束的游戏和以失败结束的游戏一样，都有可能得不到充分的开发。这并没有破坏任何东西，但它导致了当平局比输棋更可取时的次优发挥。一个快速的解决方法是在平局时将双方的 n_wins 递增一半。
MCTS(UCT) 的妙处在于，由于它的不对称性，树的选择和成长逐渐趋向于更好的移动。最后，你得到模拟次数最多的子节点，那就是你根据 MCTS 的最佳移动结果。
...
/** 从现有的统计数据中获得最佳的移动结果。 */
bestPlay(state) {
this.makeNode(state)
// 如果不是所有的子节点都被扩展，则信息不足
if (this.nodes.get(state.hash()).isFullyExpanded() === false)
throw new Error("Not enough information!")
let node = this.nodes.get(state.hash())
let allPlays = node.allPlays()
let bestPlay
let max = -Infinity
for (let play of allPlays) {
let childNode = node.childNode(play)
if (childNode.n_plays > max) {
bestPlay = play
max = childNode.n_plays
}
}
return bestPlay
}
...需要注意的是，选择最佳玩法有不同的策略。这里所采用的策略在文献中叫做 robust child，选择最高的 n_plays。另一种策略是 max child，选择最高的胜率 n_wins/n_plays。
现在，你应该可以在当前版本 index-v1.js 上运行 node index.js。但是，你不会看到很多东西。要想看到里面发生了什么，我们需要完成以下事情。
在 monte-carlo.js 文件中:
...
// 工具方法
/** 返回该节点和子节点的 MCTS 统计信息 */
getStats(state) {
let node = this.nodes.get(state.hash())
let stats = { n_plays: node.n_plays,
n_wins: node.n_wins,
children: [] }
for (let child of node.children.values()) {
if (child.node === null)
stats.children.push({ play: child.play,
n_plays: null,
n_wins: null})
else
stats.children.push({ play: child.play,
n_plays: child.node.n_plays,
n_wins: child.node.n_wins})
}
return stats
}
}
module.exports = MonteCarlo这让我们可以查询一个节点及其直接子节点的统计数据。做完这些，我们就完成了 MonteCarlo。你可以用你所拥有的东西来运行，也可以选择获取我完成的 monte-carlo.js。请注意，在我完成的版本中，bestPlay() 上有一个额外的参数来控制使用的最佳玩法策略。
现在，将 MonteCarlo.getStats() 整合到 index.js 中，或者获取我的完整版 index.js 文件。
接着运行 node index.js：
$ node index.js
player: 1
[ [ 0, 0, 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0, 0, 0 ] ]
{ n_plays: 3996,
n_wins: 1664,
children:
[ { play: Play_C4 { row: 5, col: 0 }, n_plays: 191, n_wins: 85 },
{ play: Play_C4 { row: 5, col: 1 }, n_plays: 513, n_wins: 287 },
{ play: Play_C4 { row: 5, col: 2 }, n_plays: 563, n_wins: 320 },
{ play: Play_C4 { row: 5, col: 3 }, n_plays: 1705, n_wins: 1094 },
{ play: Play_C4 { row: 5, col: 4 }, n_plays: 494, n_wins: 275 },
{ play: Play_C4 { row: 5, col: 5 }, n_plays: 211, n_wins: 97 },
{ play: Play_C4 { row: 5, col: 6 }, n_plays: 319, n_wins: 163 } ] }
chosen play: Play_C4 { row: 5, col: 3 }
player: 2
[ [ 0, 0, 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 0, 0, 0, 0 ],
[ 0, 0, 0, 1, 0, 0, 0 ] ]
{ n_plays: 6682,
n_wins: 4239,
children:
[ { play: Play_C4 { row: 5, col: 0 }, n_plays: 577, n_wins: 185 },
{ play: Play_C4 { row: 5, col: 1 }, n_plays: 799, n_wins: 277 },
{ play: Play_C4 { row: 5, col: 2 }, n_plays: 1303, n_wins: 495 },
{ play: Play_C4 { row: 4, col: 3 }, n_plays: 1508, n_wins: 584 },
{ play: Play_C4 { row: 5, col: 4 }, n_plays: 1110, n_wins: 410 },
{ play: Play_C4 { row: 5, col: 5 }, n_plays: 770, n_wins: 265 },
{ play: Play_C4 { row: 5, col: 6 }, n_plays: 614, n_wins: 200 } ] }
chosen play: Play_C4 { row: 4, col: 3 }
...
winner: 2
[ [ 0, 0, 2, 2, 2, 0, 0 ],
[ 1, 0, 2, 2, 1, 0, 1 ],
[ 2, 0, 2, 1, 1, 2, 2 ],
[ 1, 0, 1, 1, 2, 1, 1 ],
[ 2, 0, 2, 2, 1, 2, 1 ],
[ 1, 0, 2, 1, 1, 2, 1 ] ]完美！
本文主要讲述如何使用 Node.js 实现蒙特卡洛树搜索，希望大家喜欢。下一篇文章将介绍如何优化，以及蒙特卡洛树搜索（MCTS）的现状。
感谢你的阅读！
英文原文地址：https://medium.com/@quasimik/implementing-monte-carlo-tree-search-in-node-js-5f07595104df
原文作者：Michael Liu
更多编程相关知识，请访问：编程入门！！
The above is the detailed content of A brief discussion on how Node.js implements Monte Carlo tree search. For more information, please follow other related articles on the PHP Chinese website!
![[Web front-end] Node.js quick start](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
