Detailed explanation of AVL tree of Java data structure

This article brings you relevant knowledge about java, which mainly introduces the relevant knowledge about balanced binary trees (AVL trees). AVL trees are essentially binary trees with balancing functions. Find the tree, let’s take a look at it, I hope it will be helpful to everyone.

Recommended study: "java video tutorial"

Introduction of AVL tree

Searching binary trees has extremely high The search efficiency is high, but the following extreme situations will occur when searching a binary tree: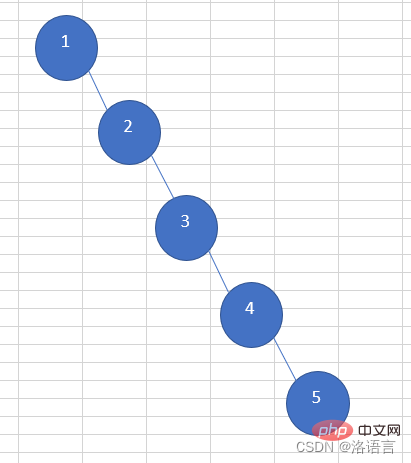

The search efficiency of such a binary tree is even lower than that of a linked list. The balanced binary tree (AVL tree) that appears based on the search binary tree solves this problem. When the absolute value of the height difference between the left and right subtrees of a node in a balanced binary tree (AVL tree) is greater than 1, their height difference will be reduced through a rotation operation.

Basic concept

The AVL tree is essentially a binary search tree. Its characteristics are:

1. itself is first a binary search tree. Search tree.
2. The absolute value (balance factor) of the difference between the heights of the left and right subtrees of each node is at most 1. In other words, the AVL tree is essentially a binary search tree (binary sorting tree, binary search tree) with balancing function.
3. When inserting a node or deleting a node, the absolute value of the height difference between the left and right subtrees of a node is greater than 1. In this case, left rotation and right rotation# are required. ##The operation makes the binary tree reach a balanced state again.

Balance Factor (balanceFactor)

The difference in height between the left subtree and the right subtree of a node
• . The BF of any node in the AVL tree can only be
-1, 0 and 1.
Basic design

The following are the simple methods and attributes required by the AVL tree:

public class AVLTree <e>>{
    class Node{
        E value;
        Node left;
        Node right;
        int height;
        public Node(){}
        public Node(E value){
            this.value = value;
            height = 1;
            left = null;
            right = null;
        }
        public void display(){
            System.out.print(this.value + " ");
        }
    }
    Node root;
    int size;
    public int size(){
        return size;
    }
    public int getHeight(Node node) {
        if(node == null) return 0;
        return node.height;
    }
    //获取平衡因子(左右子树的高度差，大小为1或者0是平衡的，大小大于1不平衡)
    public int getBalanceFactor(){
        return getBalanceFactor(root);
    }
    public int getBalanceFactor(Node node){
        if(node == null) return 0;
        return getHeight(node.left) - getHeight(node.right);
    }

    //判断一个树是否是一个平衡二叉树
    public boolean isBalance(Node node){
        if(node == null) return true;
        int balanceFactor = Math.abs(getBalanceFactor(node.left) - getBalanceFactor(node.right));
        if(balanceFactor > 1) return false;
        return isBalance(node.left) && isBalance(node.right);
    }
    public boolean isBalance(){
        return isBalance(root);
    }

    //中序遍历树
    private  void inPrevOrder(Node root){
        if(root == null) return;
        inPrevOrder(root.left);
        root.display();
        inPrevOrder(root.right);
    }
    public void inPrevOrder(){
        System.out.print("中序遍历：");
        inPrevOrder(root);
    }}</e>

RR (Left-handed)

Go to one Inserting a node into the right subtree of the right subtree of the tree causes the binary tree to become unbalanced, as shown in the figure below. Inserting 5 into the balanced binary tree causes the tree to become unbalanced. At this time, a left-turn operation is required, as follows:

The code is as follows: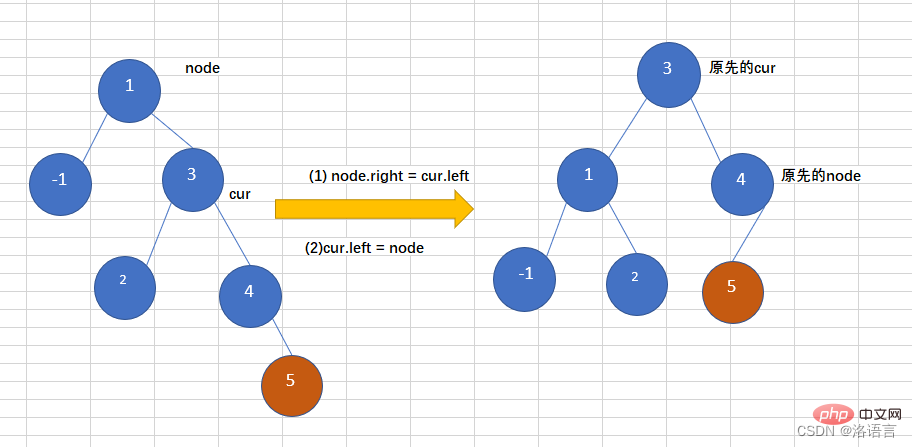

//左旋,并且返回新的根节点
    public Node leftRotate(Node node){
        System.out.println("leftRotate");
       Node cur = node.right;
       node.right = cur.left;
       cur.left = node;
       //跟新node和cur的高度
        node.height = Math.max(getHeight(node.left),getHeight(node.right)) + 1;
        cur.height = Math.max(getHeight(cur.left),getHeight(cur.right)) + 1;
        return cur;
    }

LL (right rotation)

Insert a node into the left subtree of the left subtree of an AVL tree, causing the binary tree to become unbalanced. As shown in the figure below, inserting 2 into the balanced binary tree causes the tree to become unbalanced. At this time, a left-turn operation is required, as follows:

The code is as follows: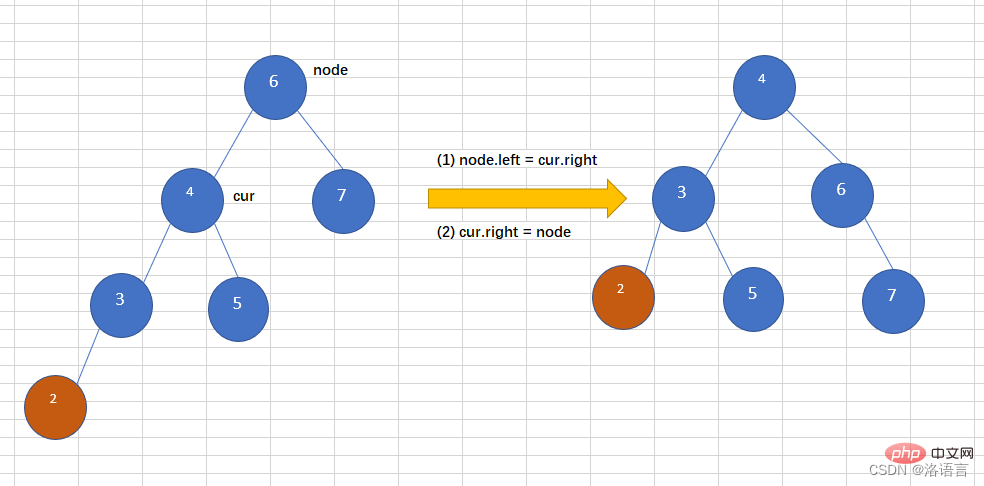

 //右旋，并且返回新的根节点
    public Node rightRotate(Node node){
        System.out.println("rightRotate");
        Node cur = node.left;
        node.left = cur.right;
        cur.right = node;
        //跟新node和cur的高度
        node.height = Math.max(getHeight(node.left),getHeight(node.right)) + 1;
        cur.height = Math.max(getHeight(cur.left),getHeight(cur.right)) + 1;
        return cur;
    }

LR (left-turn first Then rotate right)

Insert a node into the right subtree

of the AVL tree

left subtree, causing the tree to no longer be balanced. You need to perform a left rotation on the left subtree# first. ##, then right-turn the entire tree , as shown in the figure below, insert node 5.
RL (first right-turn and then left-turn)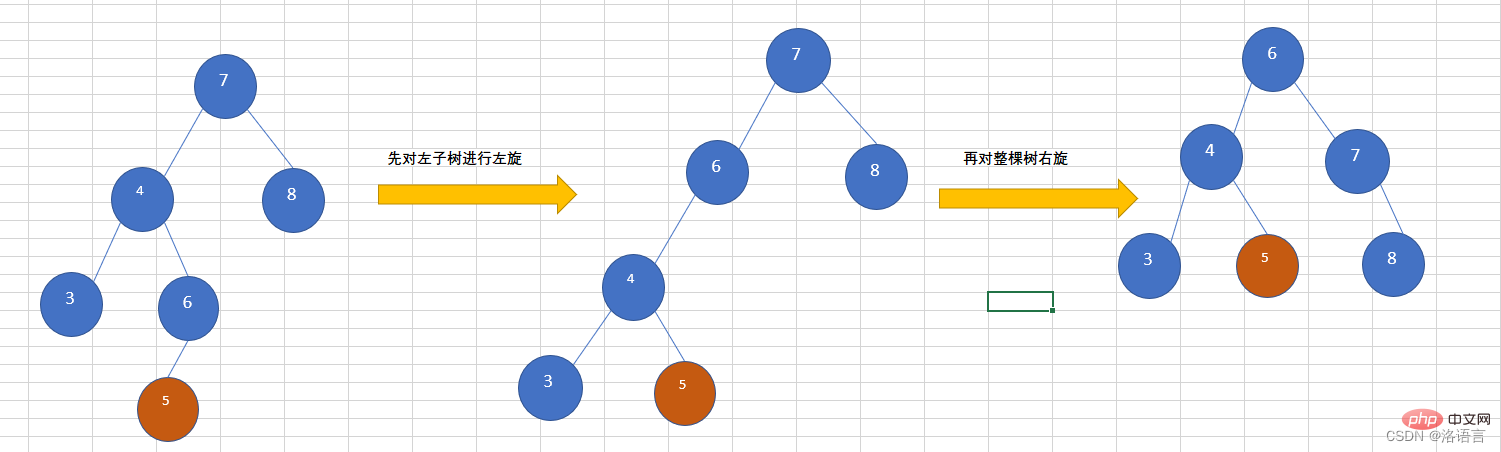

Insert a node into the left subtree

of the AVL tree

right subtree, causing the tree to become unbalanced. You need to right-rotate the

right subtree first, and then The whole tree is left-handed, as shown in the figure below, the inserted node is 2.
Add node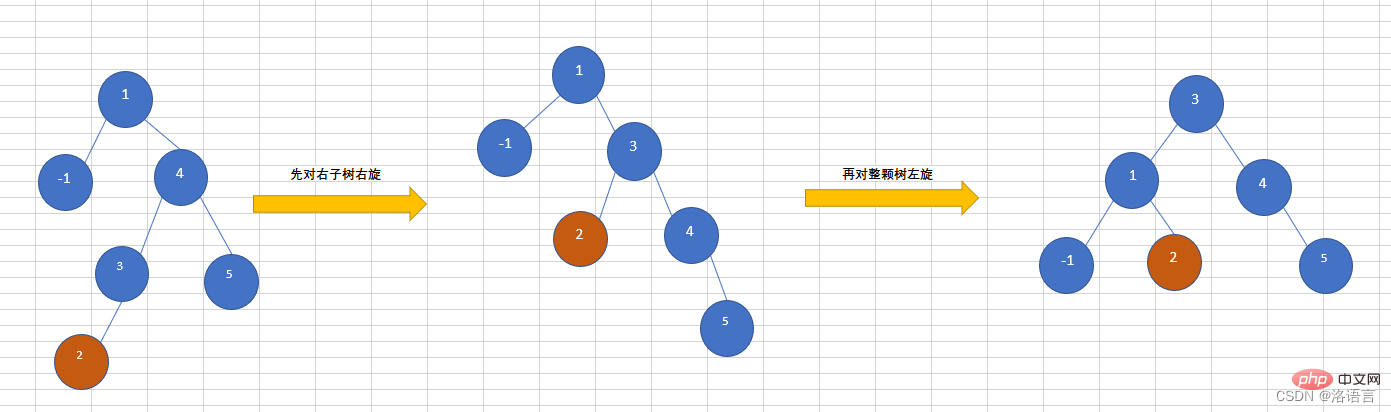

//添加元素
    public  void add(E e){
        root = add(root,e);
    }
    public Node add(Node node, E value) {
        if (node == null) {
            size++;
            return new Node(value);
        }
        if (value.compareTo(node.value) > 0) {
            node.right = add(node.right, value);
        } else if (value.compareTo(node.value)  1 && getBalanceFactor(node.left) >= 0) {
            return rightRotate(node);
        }
        //该子树不平衡且新插入节点(导致不平衡的节点)在右子树子树的右子树上，此时需要进行左旋
        else if (balanceFactor  1 && getBalanceFactor(node.left)  0
        //该子树不平衡且新插入节点(导致不平衡的节点)在右子树的左子树上，此时需要先对右子树右旋，再整个树左旋
        else if(balanceFactor  0) {
            node.right = rightRotate(node.right);
            return leftRotate(node);
        }
        return node;
    }

Delete node

 //删除节点
    public E remove(E value){
        root = remove(root,value);
        if(root == null){
            return null;
        }
        return root.value;
    }
    public Node remove(Node node, E value){
        Node retNode = null;
        if(node == null)
            return retNode;
        if(value.compareTo(node.value) > 0){
            node.right = remove(node.right,value);
            retNode = node;
        }
        else if(value.compareTo(node.value)  1 && getBalanceFactor(retNode.left) >= 0) {
            return rightRotate(retNode);
        }
        //该子树不平衡且新插入节点(导致不平衡的节点)在右子树子树的右子树上，此时需要进行左旋
        else if (balanceFactor  1 && getBalanceFactor(retNode.left)  0) {
            retNode.right = rightRotate(retNode.right);
            return leftRotate(retNode);
        }
        return  retNode;
    }

Recommended study: "

java video tutorial

"

The above is the detailed content of Detailed explanation of AVL tree of Java data structure. For more information, please follow other related articles on the PHP Chinese website!