Detailed introduction to JavaScript binary trees and various traversal algorithms

This article brings you relevant knowledge about javascript. It mainly introduces the details of JavaScript binary trees and various traversal algorithms. The article provides a detailed introduction around the topic, which has certain reference value. Friends who need it can refer to it. I hope it will be helpful to everyone.

[Related recommendations: javascript video tutorial, web front-end】

What is a binary tree

A binary tree is a tree in which each node can only have at most two child nodes, as shown in the following figure:

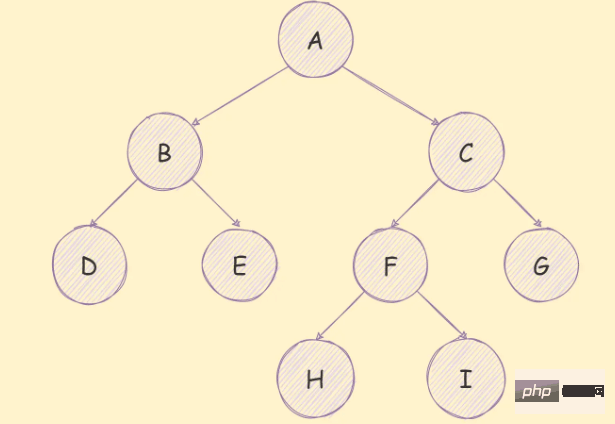
A binary tree has The following characteristics:

• There are only 2^(i-1) nodes at the i layer;
• If the depth of this binary tree is k, then the binary tree has at most 2^k-1 nodes;
• In a non-empty binary tree, if Use n0 to represent the number of leaf nodes, and n2 to be the number of non-leaf nodes with degree 2, then the two satisfy the relationship n0 = n2 1.

Full Binary Tree

If in a binary tree, Except for the leaf nodes, each degree of the remaining nodes is 2, then the binary tree is a full binary tree,

As shown in the figure below:

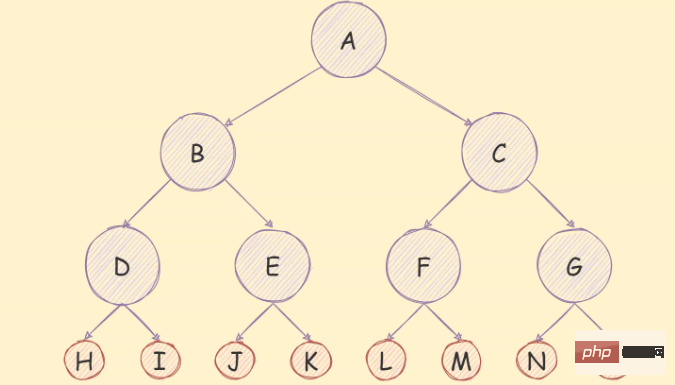
## In addition to satisfying the characteristics of ordinary binary trees, a full binary tree also has the following features: Characteristics:

The
• nth level of a full binary tree has 2^(n-1) nodes;
A full binary tree with a depth of
• k must have 2^k-1 nodes, and the number of leaf nodes is 2^(k-1);
The depth of a full binary tree with
• n nodes is log_2^(n 1).

Complete Binary Tree

If a binary tree is a full binary tree after removing the last layer, and the last node is distributed from left to right, then this A binary tree is a complete binary tree,

As shown in the figure below:

Storage of binary trees

Storage of binary trees There are two common ways, one is to use

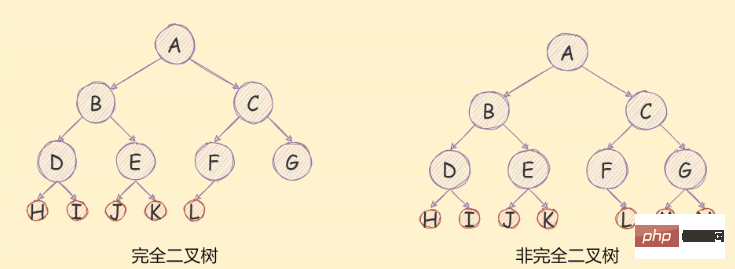
array storage, and the other is to use linked list storage.

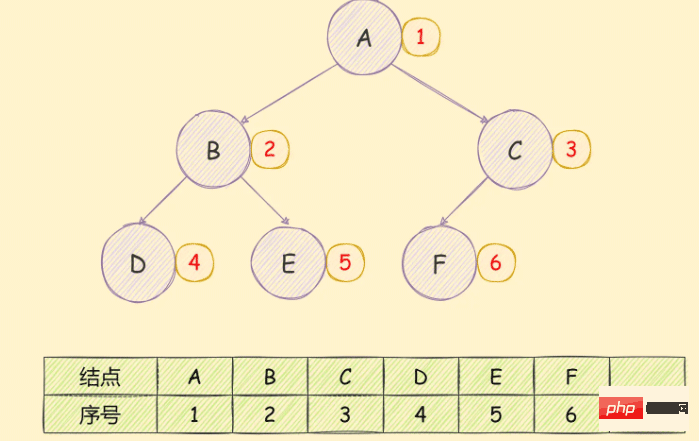
Array storage

Use arrays to store binary trees. If you encounter a complete binary tree, the storage order is from top to bottom, from left to right, as shown in the following figure:

If it is a non-complete binary tree, as shown below:

##Required First convert it into a complete binary tree, and then store it, as shown in the following figure:

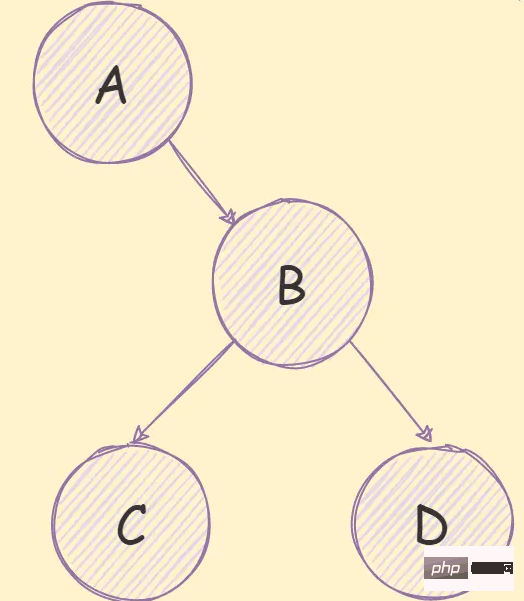
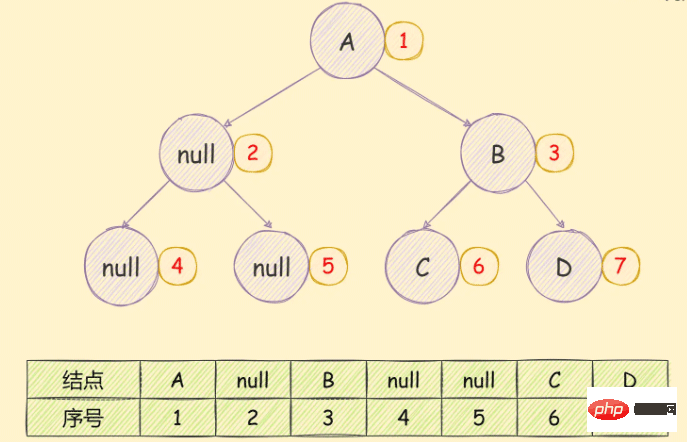You can clearly see the waste of storage space.

Linked list storage

Using linked list storage, the binary tree is usually divided into 3 parts, as shown below:

These three parts are in turn the reference to the left subtree, the data contained in the node, and the reference to the right subtree. The storage method is as shown in the figure below:

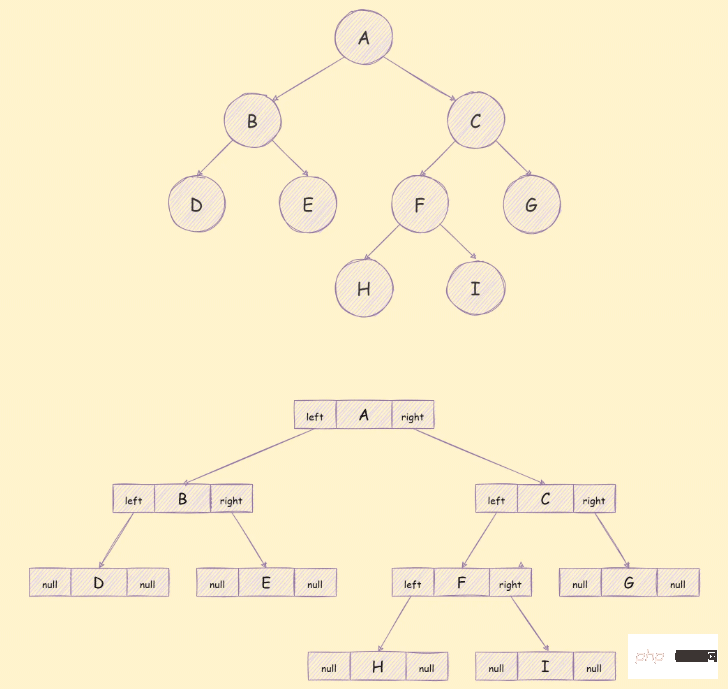Algorithms related to binary trees

The trees used for traversal in the following algorithms are as follows

:

// tree.js
const bt = {
  val: 'A',
  left: {
    val: 'B',
    left: { val: 'D', left: null, right: null },
    right: { val: 'E', left: null, right: null },
  },
  right: {
    val: 'C',
    left: {
      val: 'F',
      left: { val: 'H', left: null, right: null },
      right: { val: 'I', left: null, right: null },
    },
    right: { val: 'G', left: null, right: null },
  },
}
module.exports = bt

Depth-first traversal

The depth-first traversal of a binary tree has the same idea as the depth-first traversal of a tree. The idea is as follows:

visits the root node;

• visits the
left
• of the root node. To access the root node
right
• repeat the second and third steps

The implementation code is as follows:

const bt = {
  val: 'A',
  left: {
    val: 'B',
    left: { val: 'D', left: null, right: null },
    right: { val: 'E', left: null, right: null },
  },
  right: {
    val: 'C',
    left: {
      val: 'F',
      left: { val: 'H', left: null, right: null },
      right: { val: 'I', left: null, right: null },
    },
    right: { val: 'G', left: null, right: null },
  },
}

function dfs(root) {
  if (!root) return
  console.log(root.val)
  root.left && dfs(root.left)
  root.right && dfs(root.right) 
}
dfs(bt)
/** 结果
A B D E C F H I G
*/

Breadth-first traversal

The implementation ideas are as follows:

Create a queue and add the root node to the queue

• Exit the opponent Queue and access
• Add the
left
• and right at the head of the queue to the queue in sequence Repeat steps 2 and 3 until the queue is empty

The implementation code is as follows:

function bfs(root) {
  if (!root) return
  const queue = [root]
  while (queue.length) {
    const node = queue.shift()
    console.log(node.val)
    node.left && queue.push(node.left)
    node.right && queue.push(node.right)
  }
}
bfs(bt)
/** 结果
A B C D E F G H I
 */

Pre-order traversal

The implementation idea of ​​pre-order traversal of a binary tree is as follows:

• 访问根节点;
• 对当前节点的左子树进行先序遍历；
• 对当前节点的右子树进行先序遍历；

如下图所示：

递归方式实现如下：

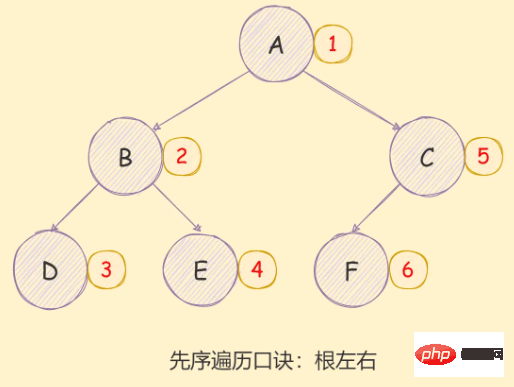
const bt = require('./tree')

function preorder(root) {
  if (!root) return
  console.log(root.val)
  preorder(root.left)
  preorder(root.right)
}
preorder(bt)
/** 结果
A B D E C F H I G
*/

迭代方式实现如下：

// 非递归版
function preorder(root) {
  if (!root) return
  // 定义一个栈，用于存储数据
  const stack = [root]
  while (stack.length) {
    const node = stack.pop()
    console.log(node.val)
    /* 由于栈存在先入后出的特性，所以需要先入右子树才能保证先出左子树 */
    node.right && stack.push(node.right)
    node.left && stack.push(node.left)
  }
}
preorder(bt)
/** 结果
A B D E C F H I G
*/

中序遍历

二叉树的中序遍历实现思想如下：

• 对当前节点的左子树进行中序遍历；
• 访问根节点;
• 对当前节点的右子树进行中序遍历；

如下图所示：

递归方式实现如下：

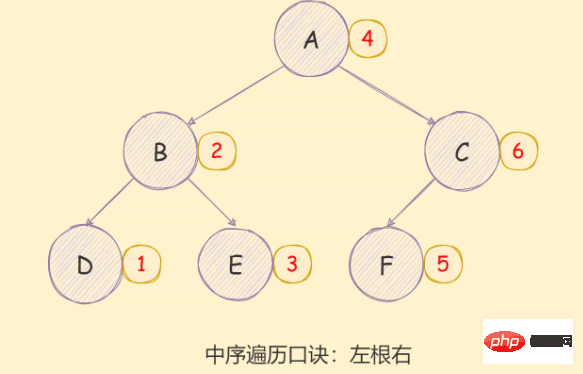
const bt = require('./tree')

// 递归版
function inorder(root) {
  if (!root) return
  inorder(root.left)
  console.log(root.val)
  inorder(root.right)
}
inorder(bt)

/** 结果
D B E A H F I C G
*/

迭代方式实现如下：

// 非递归版
function inorder(root) {
  if (!root) return
  const stack = []
  // 定义一个指针
  let p = root
  // 如果栈中有数据或者p不是null，则继续遍历
  while (stack.length || p) {
    // 如果p存在则一致将p入栈并移动指针
    while (p) {
      // 将 p 入栈，并以移动指针
      stack.push(p)
      p = p.left
    }

    const node = stack.pop()
    console.log(node.val)
    p = node.right
  }
}
inorder(bt)
/** 结果
D B E A H F I C G
*/

后序遍历

二叉树的后序遍历实现思想如下：

• 对当前节点的左子树进行后序遍历；
• 对当前节点的右子树进行后序遍历；
• 访问根节点;

如下图所示：

递归方式实现如下：

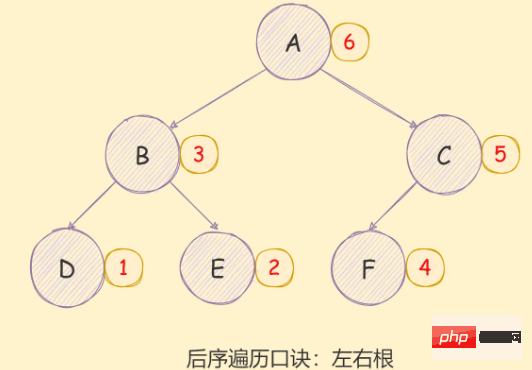
const bt = require('./tree')

// 递归版
function postorder(root) {
  if (!root) return
  postorder(root.left)
  postorder(root.right)
  console.log(root.val)
}
postorder(bt)
/** 结果
D E B H I F G C A
*/

迭代方式实现如下：

// 非递归版
function postorder(root) {
  if (!root) return
  const outputStack = []
  const stack = [root]
  while (stack.length) {
    const node = stack.pop()
    outputStack.push(node)
    // 这里先入left需要保证left后出，在stack中后出，就是在outputStack栈中先出
    node.left && stack.push(node.left)
    node.right && stack.push(node.right)
  }
  while (outputStack.length) {
    const node = outputStack.pop()
    console.log(node.val)
  }
}
postorder(bt)
/** 结果
D E B H I F G C A
*/

【相关推荐：javascript视频教程、web前端】

The above is the detailed content of Detailed introduction to JavaScript binary trees and various traversal algorithms. For more information, please follow other related articles on the PHP Chinese website!