JOIN operation of Mysql systematic analysis

This article brings you relevant knowledge about mysql. It mainly introduces the systematic discussion of the troublesome JOIN operation. This article will conduct a systematic and in-depth discussion of the JOIN operation. According to your own Based on work experience and reference to classic cases in the industry, methodologies for grammatical simplification and performance optimization are proposed in a targeted manner. I hope it will be helpful to everyone.

Recommended learning: mysql video tutorial

Preface

• I have experienced from zero to one before There are also start-up projects and massive data projects; generally speaking, how to build a safe, reliable, and stable data storage as the project develops has always been the core, most important, and most critical part of the project, and there is no such thing
• Next, I will systematically output the storage series of articles; in this article, we will first talk about one of the most troublesome connection operations in data—JOIN
• JOIN has always been a long-standing problem in SQL. When there are a little more related tables, code writing becomes very error-prone. Because of the complexity of JOIN statements, related queries have always been the weakness of BI software. There is almost no BI software that allows business users to smoothly complete multi-table associations. Inquire. The same is true for performance optimization. When there are many related tables or the amount of data is large, it is difficult to improve the performance of JOIN
• Based on the above, this article will conduct a systematic and in-depth discussion of the JOIN operation, based on my own work experience and reference Classic cases in the industry, specifically proposed methodologies for syntax simplification and performance optimization, I hope it will be helpful to everyone

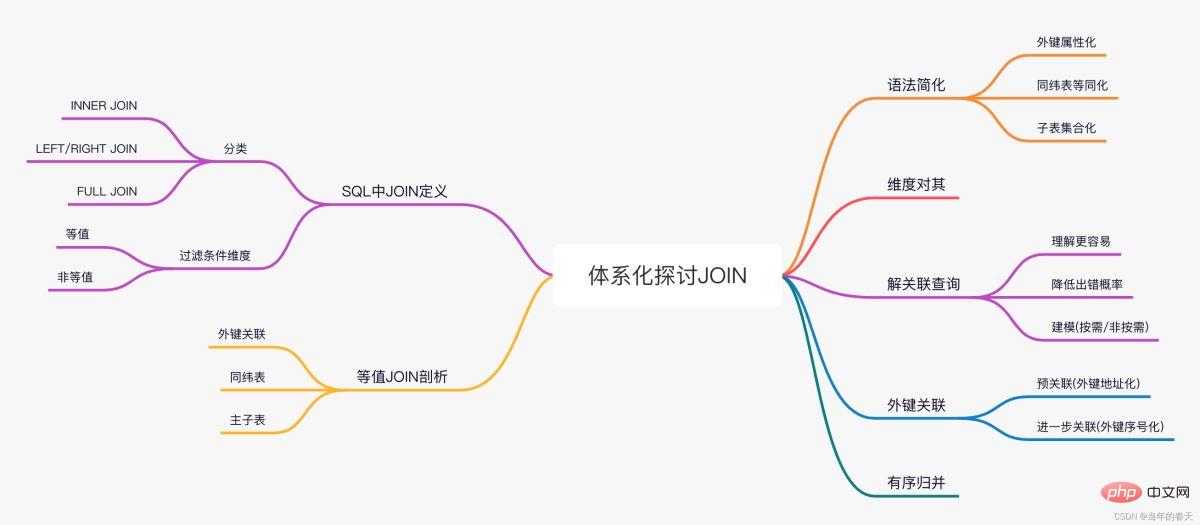
One picture overview

##SQL JOIN in

How does SQL understand the JOIN operation

SQL’s definition of JOIN

After doing a Cartesian product of two sets (tables), they are then filtered according to certain conditions. The written syntax is A JOIN B ON….

• Theoretically, the result set of the Cartesian product should be a tuple composed of two set members. However, since a set in SQL is a table, its members always have field records. Moreover, generic data types are not supported to describe tuples whose members are records, so the result set is simply processed into a collection of new records formed by merging the fields of the records in the two tables.
• This is also the original meaning of the word JOIN in English (that is, connecting the fields of two records), and does not mean multiplication (Cartesian product). However, whether the Cartesian product member is understood as a tuple or a record of a merged field does not affect our subsequent discussion.

JOIN definition

• The definition of JOIN does not specify the form of filter conditions. In theory, as long as the result set is a subset of the Cartesian product of the two source sets, All are reasonable JOIN operations.
• Example: Suppose the set A={1,2},B={1,2,3}, the result of A JOIN B ON A

JOIN Classification

• We call the filter condition for equality an equivalence JOIN, and the case where it is not an equivalence connection is called a non-equivalence JOIN. Of these two examples, the former is a non-equivalent JOIN and the latter is an equivalence JOIN.

Equal value JOIN

• The condition may be composed of multiple equations with AND relationship, the syntax form is A JOIN B ON A.ai=B.bi AND…, where ai and bi are the fields of A and B respectively.
• Experienced programmers know that in reality, the vast majority of JOINs are equivalent JOINs. Non-equivalent JOINs are much rarer, and most cases can be converted into equivalent JOINs for processing, so We focus on equivalent JOIN here, and in subsequent discussions we will mainly use tables and records instead of sets and members as examples.

Classification under null value processing rules

• According to the null value processing rules, strict equality JOIN is also called INNER JOIN, and can also be derived from LEFT JOIN There are three situations with FULL JOIN (RIGHT JOIN can be understood as the reverse association of LEFT JOIN and is no longer a separate type).
• When talking about JOIN, we generally divide it into one-to-one, one-to-many, many-to-one and many-to-many based on the number of associated records (that is, tuples that meet the filtering conditions) in the two tables. In several cases, these general terms are introduced in SQL and database materials, so they will not be repeated here.

Implementation of JOIN

Stupid method

• The easiest way to think of is to do hard traversal according to the definition, without distinguishing between equal JOIN and non-equal JOIN Value JOIN. Suppose table A has n records and table B has m records. To calculate A JOIN B ON A.a=B.b, the complexity of hard traversal will be nm, that is, nm times of calculation of filter conditions will be performed.
• Obviously this algorithm will be slower. However, reporting tools that support multiple data sources sometimes use this slow method to achieve association, because the association of the data sets in the report (that is, the filter conditions in the JOIN) will be broken up and defined in the calculation expression of the cell. It can no longer be seen that it is a JOIN operation between multiple data sets, so we can only use the traversal method to calculate these related expressions.

Database optimization for JOIN

• For equivalent JOIN, the database generally uses the HASH JOIN algorithm. That is, the records in the association table are divided into several groups according to the HASH value of their association key (corresponding to equal fields in the filter conditions, that is, A.a and B.b), and records with the same HASH value are grouped into one group. If the HASH value range is 1...k, then both tables A and B are divided into k subsets A1,...,Ak and B1,...,Bk. The HASH value of the associated key a recorded in Ai is i, and the HASH value of the associated key b recorded in Bi is also i. Then, just make a traversal connection between Ai and Bi respectively.
• Because the field values ​​must be different when the HASH is different, when i!=j, the records in Ai cannot be associated with the records in Bj. If the number of records of Ai is ni and the number of records of Bi is mi, then the number of calculations of the filter condition is SUM(ni*mi). In the most average case, ni=n/k, mi=m/k, then the total The complexity is only 1/k of the original hard traversal method, which can effectively improve computing performance!
• Therefore, if you want to speed up the multi-data source correlation report, you also need to do the correlation in the data preparation stage, otherwise the performance will drop sharply when the amount of data is slightly larger.
• However, the HASH function does not always guarantee equal splitting. If you are unlucky, a certain group may be particularly large, and the performance improvement effect will be much worse. Moreover, you cannot use too complex HASH functions, otherwise it will take more time to calculate HASH.
• When the amount of data is large enough to exceed the memory, the database will use the HASH heaping method, which is a generalization of the HASH JOIN algorithm. Traverse tables A and B, split the records into several small subsets according to the HASH value of the associated key, and cache them in external memory, which is called Heaping. Then perform memory JOIN operations between corresponding heaps. In the same way, when the HASH value is different, the key value must also be different, and the association must occur between the corresponding heaps. In this way, the JOIN of big data is converted into JOIN of several small data.
• But similarly, the HASH function has a luck problem. It may happen that a certain heap is too large to be loaded into the memory. At this time, it may be necessary to perform a second HASH heap, that is, to change the HASH function. Perform the HASH heaping algorithm again on this group of heaps that are too large. Therefore, the external memory JOIN operation may be cached multiple times, and its operation performance is somewhat uncontrollable.

JOIN under a distributed system

• JOIN under a distributed system is similar. Records are distributed to each node machine according to the HASH value of the associated key, which is called Shuffle action, and then do stand-alone JOINs separately.
• When there are many nodes, the delay caused by the network transmission volume will offset the benefits of multi-machine task sharing, so distributed database systems usually have a limit on the number of nodes. After reaching the limit, more More nodes do not result in better performance.

Analysis of equivalent JOIN

Three types of equivalent JOIN:

Foreign key association

• A certain field of table A It is associated with the primary key field of table B (the so-called field association means that equal fields must correspond to the filter conditions of equal JOIN as mentioned in the previous section). Table A is called fact table , and table B is called dimension table . The field in table A that is associated with the primary key of table B is called the foreign key of A pointing to B. B is also called the foreign key table of A.
• The primary key mentioned here refers to the logical primary key, that is, a field (group) with a unique value in the table that can be used to uniquely record a certain record. It does not necessarily have to have a primary key established on the database table.
• The foreign key table has a many-to-one relationship, and there are only JOIN and LEFT JOIN, and FULL JOIN is very rare.
• Typical cases: product transaction table and product information table.
• Obviously, the foreign key association is asymmetric. The locations of fact tables and dimension tables cannot be interchanged.

Same dimension table

• The primary key of table A is related to the primary key of table B. A and B are called each other same dimension table. Tables of the same dimension have a one-to-one relationship, and JOIN, LEFT JOIN, and FULL JOIN will all exist. However, in most data structure design solutions, FULL JOIN is relatively rare.
• Typical cases: employee table and manager table.
• Tables of the same dimension are symmetrical, and the two tables have the same status. Tables with the same dimension also form an equivalence relationship. A and B are tables with the same dimension, and B and C are tables with the same dimension. Then A and C are also tables with the same dimension.

Master and sub-tables

• The primary key of table A is associated with some of the primary keys of table B. A is called main table, and B is called Subtable . The master-child table has a one-to-many relationship. There are only JOIN and LEFT JOIN, but not FULL JOIN.
• Typical case: order and order details.
• The main and sub-tables are also asymmetrical and have clear directions.
• In the conceptual system of SQL, there is no distinction between foreign key tables and master-child tables. Many-to-one and one-to-many are only different in the direction of association from the SQL point of view, and are essentially the same thing. Indeed, orders can also be understood as foreign key tables of order details. However, we want to distinguish them here, and different means will be used when simplifying the syntax and optimizing performance in the future.
• We say that these three types of JOIN have covered the vast majority of equivalent JOIN situations. It can even be said that almost all equivalent JOINs with business significance belong to these three categories. Equivalent JOIN is limited to this Among the three situations, their scope of adaptation is hardly reduced.
• After carefully examining these three types of JOIN, we found that all associations involve primary keys, and there is no many-to-many situation. Can this situation be ignored?
• Yes! Many-to-many equivalent JOINs have almost no business meaning.
• If the associated fields when joining two tables do not involve any primary key, a many-to-many situation will occur, and in this case there will almost certainly be a larger table that combines these two Tables are related as dimension tables. For example, when the student table and the subject table are in JOIN, there will be a grade table that uses the student table and the subject table as dimension tables. JOIN with only the student table and the subject table has no business significance.
• When you find a many-to-many situation when writing a SQL statement, there is a high probability that the statement is written incorrectly! Or there is a problem with the data! This rule is very effective for eliminating JOIN errors.
• However, we have been saying "almost" without using a completely certain statement, that is to say, many-to-many will also make business sense in very rare cases. For example, when using SQL to implement matrix multiplication, a many-to-many equivalent JOIN will occur. The specific writing method can be supplemented by the reader.
• The JOIN definition of Cartesian product and then filtering is indeed very simple, and the simple connotation will have a greater extension, and can include many-to-many equivalent JOIN or even non-equivalent JOIN. However, the too simple connotation cannot fully reflect the operation characteristics of the most common equivalent JOIN. This will result in the inability to take advantage of these features when writing code and implementing operations. When the operation is more complex (involving many associated tables and nested situations), it is very difficult to write or optimize. By making full use of these features, we can create simpler writing forms and obtain more efficient computing performance, which will be gradually explained in the following content.
• Rather than defining an operation in a more general form in order to include rare cases, it would be more reasonable to define these cases as another operation.

JOIN syntax simplification

How to use the feature that associations involve primary keys to simplify JOIN code writing?

Foreign key attributeization

Example, there are two tables as follows:

employee 员工表
    id 员工编号
    name 姓名
    nationality 国籍
    department 所属部门

department 部门表
    id 部门编号
    name 部门名称
    manager 部门经理

• The primary keys of the employee table and department table are both the id field. The department field of the employee table is a foreign key pointing to the department table. The manager field of the department table is a foreign key pointing to the employee table (because the manager Also an employee). This is a very conventional table structure design.
• Now we want to ask: Which American employees have a Chinese manager? Written in SQL, it is a three-table JOIN statement:

SELECT A.* 
FROM employee A
JOIN department B ON A.department=B.id
JOIN employee C ON B.manager=C.id
WHERE A.nationality='USA' AND C.nationality='CHN'

• First, FROM employee is used to obtain employee information, and then the employee table is JOINed with department to obtain the employee's department information, and then This department table needs to be JOINd with the employee table to obtain the manager's information. In this way, the employee table needs to participate in JOIN twice. It needs to be given an alias in the SQL statement to distinguish it, and the entire sentence becomes more complicated and difficult to understand.
• If we directly understand the foreign key field as its associated dimension table record, we can write it in another way:

SELECT * FROM employee
WHERE nationality='USA' AND department.manager.nationality='CHN'

Of course, this is not a standard SQL statement.

• The bold part in the second sentence indicates the “nationality of the manager of the department” of the current employee. After we understand the foreign key field as the record of the dimension table, the field of the dimension table is understood as the attribute of the foreign key. Department.manager is the "manager of the department", and this field is still a foreign key in the department, then it The corresponding dimension table record field can continue to be understood as its attribute, and there will also be department.manager.nationality, that is, "the nationality of the manager of the department to which he belongs".
• Foreign key attribution: This object-like way of understanding is foreign key attribution, which is obviously much more natural and intuitive than the Cartesian product filtering way of understanding. JOIN of foreign key tables does not involve multiplication of the two tables. The foreign key field is only used to find the corresponding record in the dimension key table. It does not involve operations with multiplication characteristics such as Cartesian product at all.
• We agreed earlier that the associated key in the foreign key related dimension table must be the primary key. In this way, the dimension table record associated with the foreign key field of each record in the fact table is unique, that is to say, in the employee table The department field of each record is uniquely associated with a record in the department table, and the manager field of each record in the department table is also uniquely associated with a record in the employee table. This ensures that for each record in the employee table, department.manager.nationality has a unique value and can be clearly defined.
• However, there is no primary key agreement in the SQL definition of JOIN. If it is based on SQL rules, it cannot be determined that the dimension table records associated with the foreign keys in the fact table are unique, and multiple records may occur. Association, for records in the employee table, if department.manager.nationality is not clearly defined, it cannot be used.
• In fact, this kind of object-style writing is very common in high-level languages ​​​​(such as C, Java). In such languages, data is stored in the form of objects. The value of the department field in the employee table is simply an object, not a number. In fact, the primary key value of many tables itself has no business significance. It is just to distinguish records, and the foreign key field is just to find the corresponding record in the dimension table. If the foreign key field is directly an object, there is no need to use numbering. Identified. However, SQL cannot support this storage mechanism and requires the help of numbers.
• We have said that the foreign key association is asymmetric, that is, the fact table and the dimension table are not equal, and the dimension table fields can only be found based on the fact table, and not the other way around.

Equalization of tables with the same dimension

The situation of tables with the same dimension is relatively simple. Let’s start with the example. There are two tables:

employee 员工表
    id 员工编号
    name 姓名
    salary 工资
    ...

manager 经理表
    id 员工编号
    allowance 岗位津贴
    ....

• Two The primary keys of both tables are IDs, and the manager is also an employee. The two tables share the same employee number. The manager will have more attributes than ordinary employees, and another manager table will be used to store them.
• Now we want to calculate the total income (plus allowances) of all employees (including managers). JOIN will still be used when writing in SQL:

SELECT employee.id, employee.name, employy.salary+manager.allowance
FROM employee
LEFT JOIN manager ON employee.id=manager.id

But for two one-to-one tables, we can actually simply regard them as one table:

SELECT id,name,salary+allowance
FROM employee

• Similarly, according to our agreement, when the same dimension table is JOIN, the two tables are related by the primary key, and the corresponding records are uniquely corresponding. The salary allowance is uniquely calculable for each record in the employee table. It will not Ambiguity arises. This simplification is called same-dimensional table equalization.
• The relationship between tables of the same dimension is equal, and fields of other tables of the same dimension can be referenced from any table.

Collection of subtables

Orders & order details are typical main subtables:

Orders 订单表
    id 订单编号
    customer 客户
    date 日期
    ...
OrderDetail 订单明细
    id 订单编号
    no 序号
    product 订购产品
    price 价格
    ...

The primary key of the Orders table is id, and the primary key of the OrderDetail table is ( id,no), the primary key of the former is part of the latter.

Now we want to calculate the total amount of each order. Written in SQL it would look like this:

SELECT Orders.id, Orders.customer, SUM(OrderDetail.price)
FROM Orders
JOIN OrderDetail ON Orders.id=OrderDetail.id
GROUP BY Orders.id, Orders.customer

• 要完成这个运算，不仅要用到JOIN，还需要做一次GROUP BY，否则选出来的记录数太多。
• 如果我们把子表中与主表相关的记录看成主表的一个字段，那么这个问题也可以不再使用JOIN以及GROUP BY：

SELECT id, customer, OrderDetail.SUM(price)
FROM Orders

• 与普通字段不同，OrderDetail被看成Orders表的字段时，其取值将是一个集合，因为两个表是一对多的关系。所以要在这里使用聚合运算把集合值计算成单值。这种简化方式称为子表集合化。
• 这样看待主子表关联，不仅理解书写更为简单，而且不容易出错。
• 假如Orders表还有一个子表用于记录回款情况：

OrderPayment 订单回款表
    id 订单编号
    date 回款日期
    amount 回款金额
    ....

• 我们现在想知道那些订单还在欠钱，也就是累计回款金额小于订单总金额的订单。
• 简单地把这三个表JOIN起来是不对的，OrderDetail和OrderPayment会发生多对多的关系，这就错了（回忆前面提过的多对多大概率错误的说法）。这两个子表要分别先做GROUP，再一起与Orders表JOIN起来才能得到正确结果，会写成子查询的形式：

SELECT Orders.id, Orders.customer,A.x,B.y
FROM Orders
LEFT JOIN ( SELECT id,SUM(price) x FROM OrderDetail GROUP BY id ) A 
    ON Orders.id=A.id
LEFT JOIN ( SELECT id,SUM(amount) y FROM OrderPayment GROUP BY id ) B
    ON Orders.id=B.id
WHERE A.x>B.y

如果我们继续把子表看成主表的集合字段，那就很简单了：

SELECT id,customer,OrderDetail.SUM(price) x,OrderPayment.SUM(amount) y
FROM Orders WHERE x>y

• 这种写法也不容易发生多对多的错误。
• 主子表关系是不对等的，不过两个方向的引用都有意义，上面谈了从主表引用子表的情况，从子表引用主表则和外键表类似。
• 我们改变对JOIN运算的看法，摒弃笛卡尔积的思路，把多表关联运算看成是稍复杂些的单表运算。这样，相当于把最常见的等值JOIN运算的关联消除了，甚至在语法中取消了JOIN关键字，书写和理解都要简单很多。

维度对齐语法

我们再回顾前面的双子表例子的SQL：

SELECT Orders.id, Orders.customer, A.x, B.y
FROM Orders
LEFT JOIN (SELECT id,SUM(price) x FROM OrderDetail GROUP BY id ) A 
    ON Orders.id=A.id
LEFT JOIN (SELECT id,SUM(amount) y FROM OrderPayment GROUP BY id ) B
    ON Orders.id=B.id
WHERE A.x > B.y

• 那么问题来了，这显然是个有业务意义的JOIN，它算是前面所说的哪一类呢？
• 这个JOIN涉及了表Orders和子查询A与B，仔细观察会发现，子查询带有GROUP BY id的子句，显然，其结果集将以id为主键。这样，JOIN涉及的三个表（子查询也算作是个临时表）的主键是相同的，它们是一对一的同维表，仍然在前述的范围内。
• 但是，这个同维表JOIN却不能用前面说的写法简化，子查询A,B都不能省略不写。
• 可以简化书写的原因：我们假定事先知道数据结构中这些表之间的关联关系。用技术术语的说法，就是知道数据库的元数据（metadata）。而对于临时产生的子查询，显然不可能事先定义在元数据中了，这时候就必须明确指定要JOIN的表（子查询）。
• 不过，虽然JOIN的表（子查询）不能省略，但关联字段总是主键。子查询的主键总是由GROUP BY产生，而GROUP BY的字段一定要被选出用于做外层JOIN；并且这几个子查询涉及的子表是互相独立的，它们之间不会再有关联计算了，我们就可以把GROUP动作以及聚合式直接放到主句中，从而消除一层子查询：

SELECT Orders.id, Orders.customer, OrderDetail.SUM(price) x, OrderParyment.SUM(amount) y
FROM Orders 
LEFT JOIN OrderDetail GROUP BY id 
LEFT JOIN OrderPayment GROUP BY id
WHERE A.x > B.y

• 这里的JOIN和SQL定义的JOIN运算已经差别很大，完全没有笛卡尔积的意思了。而且，也不同于SQL的JOIN运算将定义在任何两个表之间，这里的JOIN，OrderDetail和OrderPayment以及Orders都是向一个共同的主键id对齐，即所有表都向某一套基准维度对齐。而由于各表的维度（主键）不同，对齐时可能会有GROUP BY，在引用该表字段时就会相应地出现聚合运算。OrderDetail和OrderPayment甚至Orders之间都不直接发生关联，在书写运算时当然就不用关心它们之间的关系，甚至不必关心另一个表是否存在。而SQL那种笛卡尔积式的JOIN则总要找一个甚至多个表来定义关联，一旦减少或修改表时就要同时考虑关联表，增大理解难度。
• 维度对齐：这种JOIN称即为维度对齐，它并不超出我们前面说过的三种JOIN范围，但确实在语法描述上会有不同，这里的JOIN不象SQL中是个动词，却更象个连词。而且，和前面三种基本JOIN中不会或很少发生FULL JOIN的情况不同，维度对齐的场景下FULL JOIN并不是很罕见的情况。
• 虽然我们从主子表的例子抽象出维度对齐，但这种JOIN并不要求JOIN的表是主子表（事实上从前面的语法可知，主子表运算还不用写这么麻烦），任何多个表都可以这么关联，而且关联字段也完全不必要是主键或主键的部分。
• 设有合同表，回款表和发票表：

Contract 合同表
    id 合同编号
    date 签订日期
    customer 客户
    price 合同金额
    ...

Payment 回款表
    seq 回款序号
    date 回款日期
    source 回款来源
    amount 金额
    ...

Invoice 发票表
    code 发票编号
    date 开票日期
    customer 客户
    amount 开票金额
    ...

现在想统计每一天的合同额、回款额以及发票额，就可以写成：

SELECT Contract.SUM(price), Payment.SUM(amount), Invoice.SUM(amount) ON date
FROM Contract GROUP BY date
FULL JOIN Payment GROUP BY date
FULL JOIN Invoice GROUP BY date

• 这里需要把date在SELECT后单独列出来表示结果集按日期对齐。
• 这种写法，不必关心这三个表之间的关联关系，各自写各自有关的部分就行，似乎这几个表就没有关联关系，把它们连到一起的就是那个要共同对齐的维度（这里是date）。
• 这几种JOIN情况还可能混合出现。
• 继续举例，延用上面的合同表，再有客户表和销售员表

Customer 客户表
    id 客户编号
    name 客户名称
    area 所在地区
    ...

Sales 销售员表
    id 员工编号
    name 姓名
    area 负责地区
    ...

• 其中Contract表中customer字段是指向Customer表的外键。
• 现在我们想统计每个地区的销售员数量及合同额：

SELECT Sales.COUNT(1), Contract.SUM(price) ON area
FROM Sales GROUP BY area
FULL JOIN Contract GROUP BY customer.area

• 维度对齐可以和外键属性化的写法配合合作。
• 这些例子中，最终的JOIN都是同维表。事实上，维度对齐还有主子表对齐的情况，不过相对罕见，我们这里就不深入讨论了。
• 另外，目前这些简化语法仍然是示意性，需要在严格定义维度概念之后才能相应地形式化，成为可以解释执行的句子。
• 我们把这种简化的语法称为DQL（Dimensional Query Languange），DQL是以维度为核心的查询语言。我们已经将DQL在工程上做了实现，并作为润乾报表的DQL服务器发布出来，它能将DQL语句翻译成SQL语句执行，也就是可以在任何关系数据库上运行。
• 对DQL理论和应用感兴趣的读者可以关注乾学院上发布的论文和相关文章。

解决关联查询

多表JOIN问题

• 我们知道，SQL允许用WHERE来写JOIN运算的过滤条件（回顾原始的笛卡尔积式的定义），很多程序员也习惯于这么写。
• 当JOIN表只有两三个的时候，那问题还不大，但如果JOIN表有七八个甚至十几个的时候，漏写一个JOIN条件是很有可能的。而漏写了JOIN条件意味着将发生多对多的完全叉乘，而这个SQL却可以正常执行，会有以下两点危害：
  • 一方面计算结果会出错:回忆一下以前说过的，发生多对多JOIN时，大概率是语句写错了
  • 另一方面，如果漏写条件的表很大，笛卡尔积的规模将是平方级的，这极有可能把数据库直接“跑死”！

简化JOIN运算好处：

• 一个直接的效果显然是让语句书写和理解更容易
• 外键属性化、同维表等同化和子表集合化方案直接消除了显式的关联运算，也更符合自然思维
• 维度对齐则可让程序员不再关心表间关系，降低语句的复杂度
• 简化JOIN语法的好处不仅在于此，还能够降低出错率，采用简化后的JOIN语法，就不可能发生漏写JOIN条件的情况了。因为对JOIN的理解不再是以笛卡尔积为基础，而且设计这些语法时已经假定了多对多关联没有业务意义，这个规则下写不出完全叉乘的运算。
• 对于多个子表分组后与主表对齐的运算，在SQL中要写成多个子查询的形式。但如果只有一个子表时，可以先JOIN再GROUP，这时不需要子查询。有些程序员没有仔细分析，会把这种写法推广到多个子表的情况，也先JOIN再GROUP，可以避免使用子查询，但计算结果是错误的。
• 使用维度对齐的写法就不容易发生这种错误了，无论多少个子表，都不需要子查询，一个子表和多个子表的写法完全相同。

关联查询

• 重新看待JOIN运算，最关键的作用在于实现关联查询。
• 当前BI产品是个热门，各家产品都宣称能够让业务人员拖拖拽拽就完成想要的查询报表。但实际应用效果会远不如人意，业务人员仍然要经常求助于IT部门。造成这个现象的主要原因在于大多数业务查询都是有过程的计算，本来也不可能拖拽完成。但是，也有一部分业务查询并不涉及多步过程，而业务人员仍然难以完成。
• 这就是关联查询，也是大多数BI产品的软肋。在之前的文章中已经讲过为什么关联查询很难做，其根本原因就在于SQL对JOIN的定义过于简单。
• 结果，BI产品的工作模式就变成先由技术人员构建模型，再由业务人员基于模型进行查询。而所谓建模，就是生成一个逻辑上或物理上的宽表。也就是说，建模要针对不同的关联需求分别实现，我们称之为按需建模，这时候的BI也就失去敏捷性了。
• 但是，如果我们改变了对JOIN运算的看法，关联查询可以从根本上得到解决。回忆前面讲过的三种JOIN及其简化手段，我们事实上把这几种情况的多表关联都转化成了单表查询，而业务用户对于单表查询并没有理解障碍。无非就是表的属性（字段）稍复杂了一些：可能有子属性（外键字段指向的维表并引用其字段），子属性可能还有子属性（多层的维表），有些字段取值是集合而非单值（子表看作为主表的字段）。发生互相关联甚至自我关联也不会影响理解（前面的中国经理的美国员工例子就是互关联），同表有相同维度当然更不碍事（各自有各自的子属性）。
• 在这种关联机制下，技术人员只要一次性把数据结构（元数据）定义好，在合适的界面下（把表的字段列成有层次的树状而不是常规的线状），就可以由业务人员自己实现JOIN运算，不再需要技术人员的参与。数据建模只发生于数据结构改变的时刻，而不需要为新的关联需求建模，这也就是非按需建模，在这种机制支持下的BI才能拥有足够的敏捷性。

外键预关联

• 我们再来研究如何利用JOIN的特征实现性能优化，这些内容的细节较多，我们挑一些易于理解的情况来举例，更完善的连接提速算法可以参考乾学院上的《性能优化》图书和SPL学习资料中的性能优化专题文章。

全内存下外键关联情况

设有两个表：

customer 客户信息表
    key 编号
    name 名称
    city 城市
    ...

orders 订单表
    seq 序号
    date 日期
    custkey 客户编号
    amount 金额
    ...

• 其中orders表中的custkey是指向customer表中key字段的外键，key是customer表的主键。
• 现在我们各个城市的订单总额（为简化讨论，就不再设定条件了），用SQL写出来：

SELECT customer.city, SUM(orders.amount)
FROM orders
JOIN customer ON orders.custkey=customer.key
GROUP BY customer.city

• 数据库一般会使用HASH JOIN算法，需要分别两个表中关联键的HASH值并比对。
• 我们用前述的简化的JOIN语法（DQL）写出这个运算：

SELECT custkey.city, SUM(amount)
FROM orders
GROUP BY custkey.city

• 这个写法其实也就预示了它还可以有更好的优化方案，下面来看看怎样实现。
• 如果所有数据都能够装入内存，我们可以实现外键地址化。
• 将事实表orders中的外键字段custkey，转换成维表customer中关联记录的地址，即orders表的custkey的取值已经是某个customer表中的记录，那么就可以直接引用记录的字段进行计算了。
• 用SQL无法描述这个运算的细节过程，我们使用SPL来描述、并用文件作为数据源来说明计算过程：

	A
1	=file(“customer.btx”).import@b()
2	>A1.keys@i(key)
3	=file(“orders.btx”).import@b()
4	>A3.switch(custkey,A1)
5	=A3.groups(custkey.city;sum(amount))

• A1 reads the customer table, and A2 sets the primary key and creates an index for the customer table.
• A3 reads the order table, and A4's action is to convert the foreign key field custkey of A3 into the corresponding record of A1. After execution, the order table field custkey will become a record of the customer table. A2 builds an index to make the switch faster, because the fact table is usually much larger than the dimension table, and this index can be reused many times.
• A5 can perform group summary. When traversing the order table, since the value of the custkey field is now a record, you can directly use the . operator to reference its field, and custkey.city can be executed normally.
• After completing the switch action in A4, the content stored in the custkey field of fact table A3 in memory is already the address of a record in dimension table A1. This action is called foreign key addressization. At this time, when referencing the dimension table fields, they can be retrieved directly without using the foreign key value to search in A1. This is equivalent to getting the dimension table fields in a constant time, avoiding HASH value calculation and comparison.
• However, A2 generally uses the HASH method to build the primary key index and calculates the HASH value for the key. When A4 converts the address, it also calculates the HASH value of the custkey and compares it with the HASH index table of A2. If only one correlation operation is performed, the calculation amount of the address scheme and the traditional HASH segmentation scheme are basically the same, and there is no fundamental advantage.
• But the difference is that if the data can be placed in the memory, this address can be reused once converted. That is to say, A1 to A4 only need to be done once, and the associated operation on these two fields will be done next time. There is no need to calculate HASH values ​​and compare them, and the performance can be greatly improved.
• This is possible by taking advantage of the uniqueness of the foreign key association mentioned earlier in the dimension table. A foreign key field value will only uniquely correspond to one dimension table record. Each custkey can be Convert it to the only record of A1 it corresponds to. However, if we continue to use the definition of JOIN in SQL, we cannot assume that the foreign key points to the uniqueness of the record, and this representation cannot be used. Moreover, SQL does not record the data type of address. As a result, the HASH value must be calculated and compared for each association.
• Moreover, if there are multiple foreign keys in the fact table pointing to multiple dimension tables, the traditional HASH segmented JOIN solution can only parse one at a time. If there are multiple JOINs, multiple actions must be performed. After each association, the intermediate results need to be kept for the next round of use. The calculation process is much more complicated and the data will be traversed multiple times. When facing multiple foreign keys, the foreign key addressization scheme only needs to traverse the fact table once, without intermediate results, and the calculation process is much clearer.
• Another point is that memory is originally very suitable for parallel calculations, but the HASH segmented JOIN algorithm is not easy to parallelize. Even if the data is segmented and HASH values ​​are calculated in parallel, records with the same HASH value must be grouped together for the next round of comparison, and shared resource preemption will occur, which will sacrifice many advantages of parallel computing. Under the foreign key JOIN model, the status of the two related tables is not equal. After clearly distinguishing the dimension table and the fact table, parallel calculations can be performed by simply segmenting the fact table.
• After transforming the HASH segmentation technology with reference to the foreign key attribute scheme, it can also improve the one-time parsing and parallel capabilities of multiple foreign keys to a certain extent. Some databases can implement this optimization at the engineering level. However, this optimization is not a big problem when there are only two tables JOIN. When there are many tables and various JOINs mixed together, it is not easy for the database to identify which table should be used as the fact table for parallel traversal, and other tables should be traversed in parallel. When creating a HASH index as a dimension table, optimization is not always effective. Therefore, we often find that when the number of JOIN tables increases, the performance will drop sharply (it often occurs when there are four or five tables, and the result set does not increase significantly). After the foreign key concept is introduced from the JOIN model, when this kind of JOIN is specifically processed, the fact table and the dimension table can always be distinguished. More JOIN tables will only lead to a linear decrease in performance.
• In-memory database is currently a hot technology, but the above analysis shows that it is difficult for an in-memory database using the SQL model to perform JOIN operations quickly!

Further foreign key association

• We continue to discuss foreign key JOIN and continue to use the example in the previous section.
• When the amount of data is too large to fit into the memory, the aforementioned addressing method is no longer effective, because the pre-calculated address cannot be saved in external memory.
• Generally speaking, the dimension table pointed to by the foreign key has a smaller capacity, while the growing fact table is much larger. If the memory can still hold the dimension table, we can use the temporary pointing method to handle foreign keys.

##1= file(“customer.btx”).import@b()2=file(“orders.btx”).cursor@b()3>A2.switch(custkey,A1:#)4=A2 .groups(custkey.city;sum(amount))

• The first two steps are the same as those in full memory. The address conversion in step 4 is performed while reading, and the conversion results cannot be retained and reused. The HASH and ratio must be calculated again the next time the association is made. Yes, the performance is worse than the full memory solution. In terms of calculation amount, compared with the HASH JOIN algorithm, there is one less calculation of the HASH value of the dimension table. If this dimension table is often reused, it will be cheaper, but because the dimension table is relatively small, the overall advantage is not great. However, this algorithm also has the characteristics of a full-memory algorithm that can parse all foreign keys at once and is easy to parallelize. In actual scenarios, it still has a greater performance advantage than the HASH JOIN algorithm.

Foreign key serialization

Based on this algorithm, we can also make a variant: foreign key serialization.

If we can convert the primary keys of the dimension table into natural numbers starting from 1, then we can use the serial number to directly locate the dimension table record, without the need to calculate and compare HASH values, so that we can obtain something like Performance of addressing in full memory.

	A

	A
1	=file(“customer.btx”). import@b()
2	=file(“orders.btx”).cursor@b()
3	>A2.switch(custkey,A1:#)
4	=A2.groups(custkey.city;sum( amount))

• When the primary key of the dimension table is a serial number, there is no need to do the original step 2 of building a HASH index.
• Foreign key serialization is essentially equivalent to addressing in external memory. This solution requires converting the foreign key fields in the fact table into serial numbers, which is similar to the addressization process during full-memory operations. This precomputation can also be reused. It should be noted that when major changes occur in the dimension table, the foreign key fields of the fact table need to be organized synchronously, otherwise the correspondence may be misaligned. However, the frequency of general dimension table changes is low, and most actions are additions and modifications rather than deletions, so there are not many situations where the fact table needs to be reorganized. For details on engineering, you can also refer to the information in the Cadre Academy.
• SQL uses the concept of unordered sets. Even if we serialize foreign keys in advance, the database cannot take advantage of this feature. The mechanism of rapid positioning by serial numbers cannot be used on unordered sets, and only index search can be used. , and the database does not know that the foreign key is serialized, and will still calculate the HASH value and comparison.
• What if the dimension table is too large to fit in the memory?
• If we carefully analyze the above algorithm, we will find that the access to the fact table is continuous, but the access to the dimension table is random. When we discussed the performance characteristics of hard disks before, we mentioned that external memory is not suitable for random access, so the dimension tables in external memory can no longer use the above algorithm.
• Dimension tables in external storage can be sorted and stored by primary key in advance, so that we can continue to use the feature that the associated key of the dimension table is the primary key to optimize performance.
• If the fact table is small and can be loaded in memory, then using foreign keys to associate dimension table records will actually become a (batch) external storage search operation. As long as there is an index on the primary key on the dimension table, it can be searched quickly. This can avoid traversing large dimension tables and obtain better performance. This algorithm can also resolve multiple foreign keys simultaneously. SQL does not distinguish between dimension tables and fact tables. When faced with two tables, one large and one small, the optimized HASH JOIN will no longer do heap caching. The small table will usually be read into the memory and the large table will be traversed. This will still cause If there is an action of traversing a large dimension table, the performance will be much worse than the external memory search algorithm just mentioned.
• If the fact table is also very large, you can use the one-sided heaping algorithm. Because the dimension table has been ordered by the associated key (i.e., primary key), it can be easily divided logically into several segments and take out the boundary value of each segment (the maximum and minimum value of the primary key of each segment), and then divide the fact table into piles according to these boundary values. , each pile can be associated with each segment of the dimension table. In the process, only the fact table side needs to be physically cached, and the dimension table does not need to be physically cached. Moreover, the HASH function is not used, and segmentation is used directly. It is impossible for the HASH function to be unlucky and cause secondary segmentation. Heap, performance is controllable. The HASH heaping algorithm of the database will do physical heaping cache for both large tables, that is, bilateral heaping. It may also happen that the HASH function is unlucky, resulting in secondary heaping, and the performance is worse than unilateral heaping. Too much and still uncontrollable.

Use the power of clusters to solve the problem of large dimension tables.

• If the memory of one machine cannot be accommodated, you can build several more machines to accommodate it, and store the dimension tables on multiple machines segmented according to the primary key values ​​to form a cluster dimension table, then you can continue to use the above algorithm for memory dimension tables, and you can also get the benefits of parsing multiple foreign keys at one time and being easy to parallelize. Similarly, cluster dimension tables can also use serialization technology. Under this algorithm, the fact table does not need to be transmitted, the amount of network transmission generated is not large, and there is no need to cache data locally on the node. However, dimension tables cannot be distinguished under the SQL system. The HASH splitting method requires shuffling both tables, and the amount of network transmission is much larger.
• The details of these algorithms are still somewhat complicated and cannot be explained in detail here due to space limitations. Interested readers can check the information on Qian Academy.

Ordered merge

Join optimization and speed-up methods for same-dimensional tables & master-child tables

• We discussed previously the computational complexity of the HASH JOIN algorithm (That is, the number of comparisons of associated keys) is SUM(nimi), which is much smaller than the complexity of full traversal nm, but it depends on the luck of the HASH function.
• If both tables are sorted for the associated keys, then we can use the merge algorithm to process the association. The complexity at this time is n m; when n and m are both large (generally far larger (in the value range of the HASH function), this number will also be much smaller than the complexity of the HASH JOIN algorithm. There are many materials introducing the details of the merging algorithm, so I won’t go into details here.
• However, this method cannot be used when foreign key JOIN is used, because the fact table may have multiple foreign key fields that need to participate in the association, and it is impossible to order the same fact table for multiple fields at the same time.
• The same dimension table and master-child table can be used! Because the same-dimensional tables and master-child tables are always related to the primary key or a part of the primary key, we can sort the data in these related tables according to their primary keys in advance. Although the cost of sorting is higher, it is one-time. Once the sorting is completed, you can always use the merge algorithm to implement JOIN in the future, and the performance can be improved a lot.
• This still takes advantage of the fact that the associated key is the primary key (and its parts).
• Ordered merge is particularly effective for big data.Master and sub-tables such as orders and their details are growing fact tables, which often accumulate to a very large size over time and can easily exceed the memory capacity.
• The HASH heaping algorithm for external storage big data needs to generate a lot of cache. The data is read twice and written once in the external storage, which causes a lot of IO overhead. In the merge algorithm, the data in both tables only needs to be read once, without writing. Not only is the calculation amount of the CPU reduced, but the IO amount of the external memory is also significantly reduced. Moreover, very little memory is required to execute the merge algorithm. As long as several cache records are kept in memory for each table, it will hardly affect the memory requirements of other concurrent tasks. HASH heaping requires larger memory and reads more data each time to reduce the number of heaping times.
• SQL adopts the JOIN operation defined by Cartesian product and does not distinguish between JOIN types. Without assuming that some JOINs are always targeted at the primary key, there is no way to take advantage of this feature from the algorithm level and can only be optimized at the engineering level. . Some databases will check whether the data table is physically ordered for the associated fields, and if so, use the merge algorithm. However, relational databases based on the concept of unordered sets will not deliberately ensure the physical orderliness of the data, and many operations will destroy the merge. Implementation conditions of the algorithm. Using indexes can achieve logical ordering of data, but the traversal efficiency will still be greatly reduced when the data is physically disordered.
• The premise of ordered merge is to sort the data according to the primary key, and this type of data is often continuously appended. In principle, it must be sorted again after each append, and we know that the cost of sorting big data is usually very high. This Will it make it difficult to append data? In fact, the process of appending data and then adding it is also an ordered merge. The new data is sorted separately and merged with the ordered historical data. The complexity is linear, which is equivalent to rewriting all the data once, unlike conventional Big data sorting requires cached writing and reading. Making some optimization actions in engineering can also eliminate the need to rewrite everything every time, further improving maintenance efficiency. These are introduced in the Cadre Academy.

Segmented parallelism

• The benefit of ordered merge is that it is easy to perform segmented parallelization.
• Modern computers all have multi-core CPUs, and SSD hard drives also have strong concurrency capabilities. Using multi-threaded parallel computing can significantly improve performance. However, it is difficult to achieve parallelism with traditional HASH heaping technology. When multi-threads do HASH heaping, they need to write data to a certain heap at the same time, causing shared resource conflicts; and in the second step, when realizing the association of a certain group of heaps, a large amount of money will be consumed. memory, does not allow implementing larger amounts of parallelism.
• When using ordered merge to implement parallel calculations, the data needs to be divided into multiple segments. Single table segmentation is relatively simple, but two related table segments must be aligned synchronously. Otherwise, the data of the two tables will be misaligned during the merge. Correct calculation results cannot be obtained, but ordering the data can ensure high-performance synchronously aligned segmentation.
• First divide the main table (the larger one is enough for tables with the same dimension, other discussions will not be affected) into several segments, read the primary key value of the first record in each segment, and then use these key values Go to the subtable and use the dichotomy method to find the position (because it is also ordered), so as to obtain the segmentation point of the subtable. This ensures that the segments of the main and sub-tables are synchronously aligned.
• Because the key values ​​are in order, the record key values ​​in each segment of the main table belong to a certain continuous interval. Records with key values ​​outside the interval will not be in this segment, and records with key values ​​within the interval must be in In this section, the record key values ​​corresponding to the segments in the subtable also have this feature, so misalignment will not occur; and also because the key values ​​are in order, an efficient binary search can be performed in the subtable to quickly locate the segmentation point. That is, the order of data ensures the rationality and efficiency of segmentation, so that parallel algorithms can be executed with confidence.
• Another characteristic of the primary key association relationship between master and child tables is that the child table will only be associated with one primary table on the primary key (in fact, there are also tables with the same dimension, but it is easy to explain using the master and child tables), it will not There are multiple master tables that are unrelated to each other (there may be master tables of master tables). At this time, you can also use the integrated storage mechanism to store the sub-table records as field values ​​of the main table. In this way, on the one hand, the amount of storage is reduced (the associated key only needs to be stored once), and it is equivalent to pre-making the association, and there is no need to compare it again. For big data, better performance can be obtained.
• We have implemented the above performance optimization methods in esProc SPL and applied them in actual scenarios, and achieved very good results. SPL is now open source. Readers can go to the official websites and forums of Shusu Company or Runqian Company to download and obtain more information.

Recommended learning: mysql video tutorial

The above is the detailed content of JOIN operation of Mysql systematic analysis. For more information, please follow other related articles on the PHP Chinese website!