 Java
Java
 javaTutorial
javaTutorial
 The principle and implementation of Prime algorithm in Java (summary sharing)
The principle and implementation of Prime algorithm in Java (summary sharing)
The principle and implementation of Prime algorithm in Java (summary sharing)
This article brings you relevant knowledge about java. The Prime algorithm is an exhaustive search algorithm to construct a minimum spanning tree from a connected graph. This article mainly introduces the principle and implementation of the Prime algorithm in Java. If you are interested, you can learn about it.

java video tutorial"
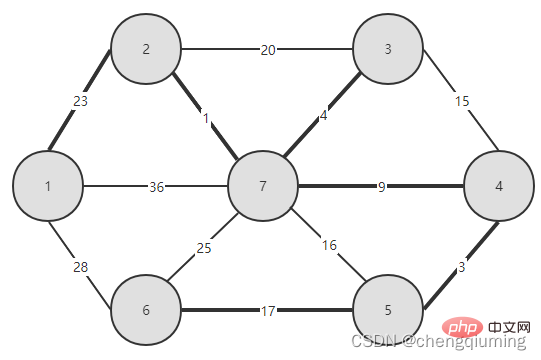
Introduction to Prim algorithm1. The finishing touchIn the process of generating a tree, the nodes already in the spanning tree are regarded as a set, the remaining nodes are regarded as another set, and the edge with the smallest weight is selected from the edges connecting the two sets. Can. 2. Algorithm introduction
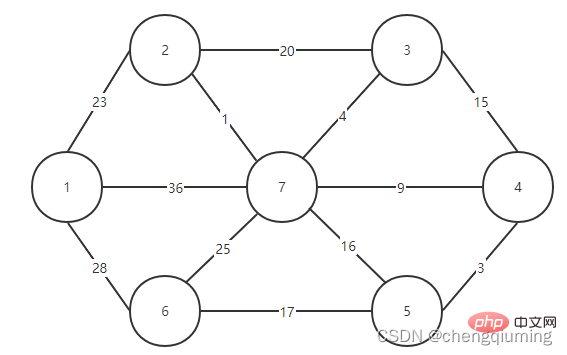
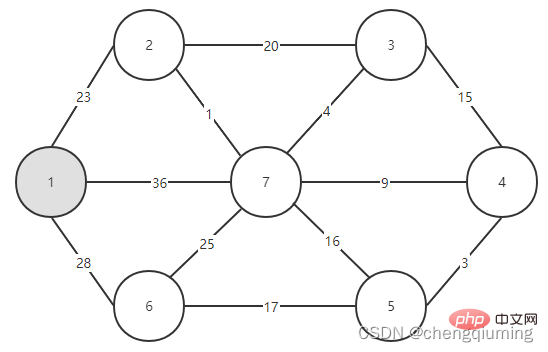
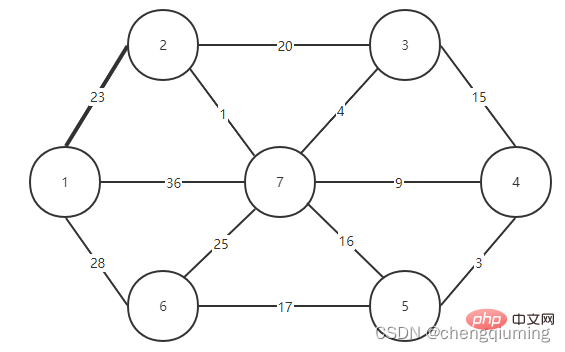
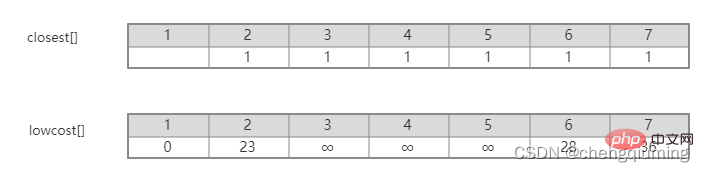
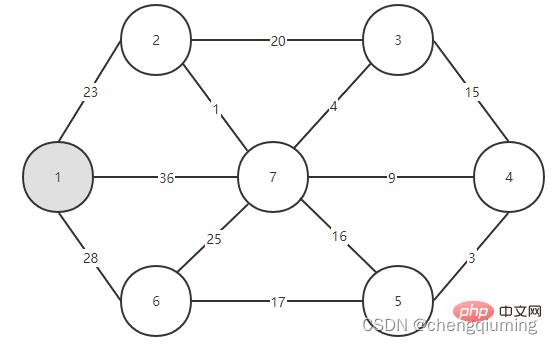
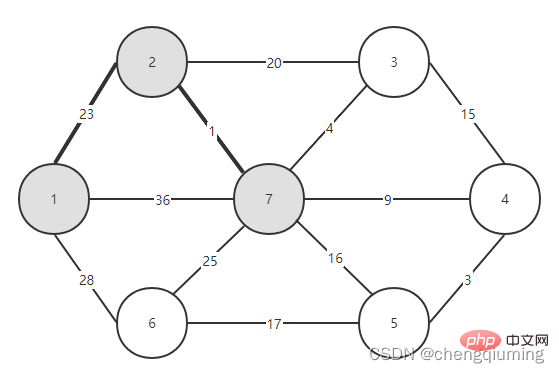
2 Find the node with the smallest lowcost, corresponding to t=2. The selected edges and nodes are as shown below.
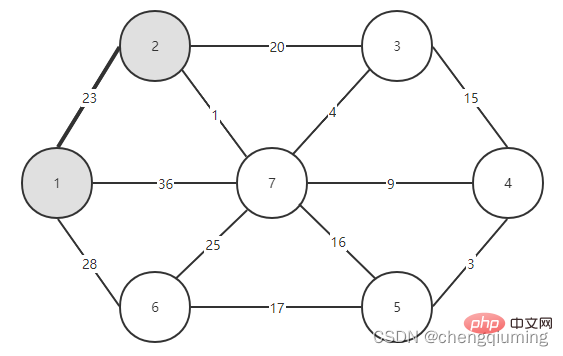
3 Add to set U. Add node t to the set U, U={1,2}, and update V-U={3,4,5,6,7}
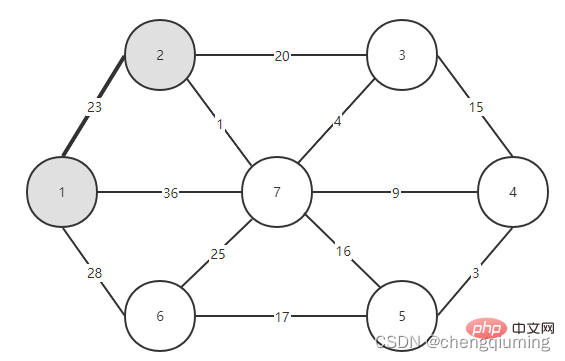
4 at the same time. For each adjacent point j of t in the set V-U, it can be updated with the help of t. The adjacent points of node 2 are node 3 and node 7.
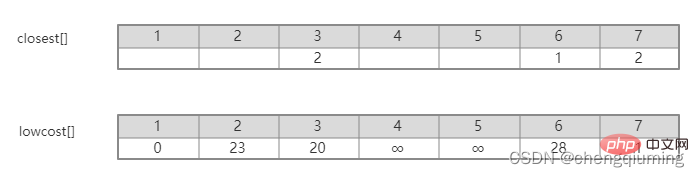
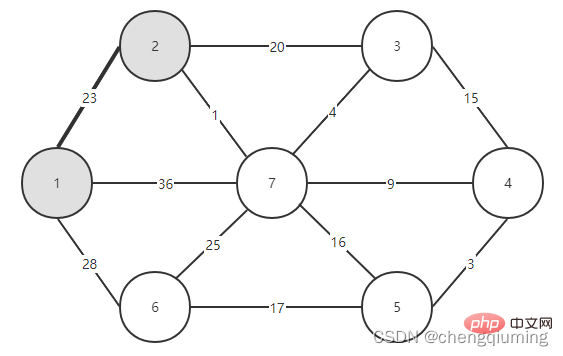
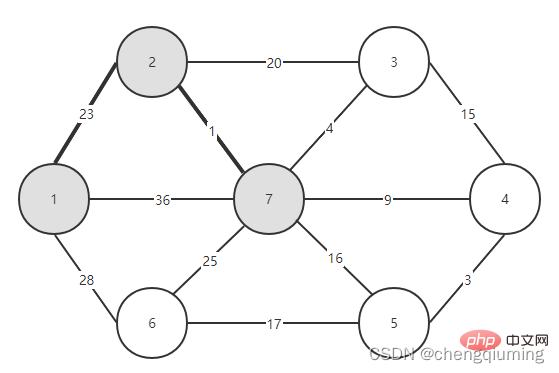
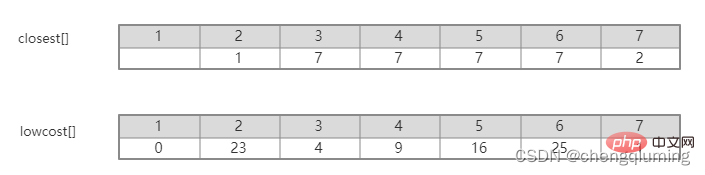
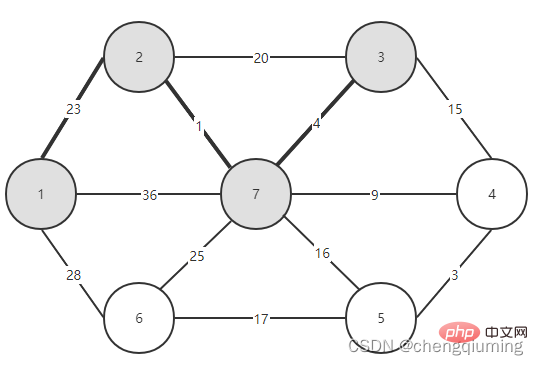
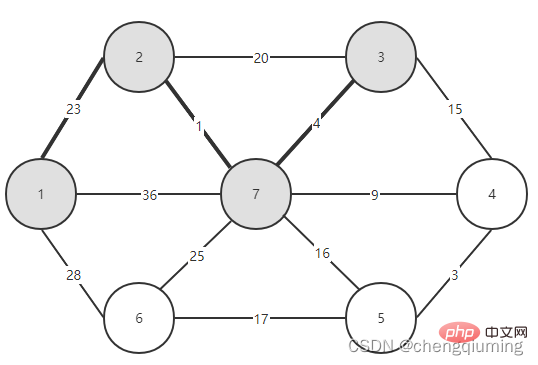
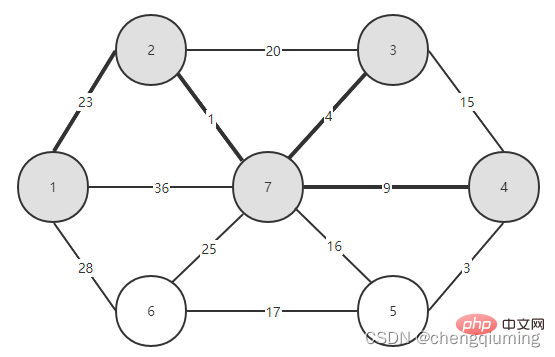
C[2][3]=20 C[2][7]=1 Updated closest[] and lowcost[] as shown below. The updated set is as shown below: 5 Find the node with the smallest lowcost, and the corresponding t= 7. The selected edges and nodes are as shown below. 6 Add to set U. Add node t to the set U, U={1,2,7}, and update V-U={3,4,5,6} 7 at the same time. For each adjacent point j of t in the set V-U, it can be updated with the help of t. The adjacent points of node 7 are nodes 3, 4, 5, and 6. The updated closest[] and lowcost[] are as shown below shown. The updated set is shown in the figure below: 16 at the same time. For each adjacent point j of t in the set V-U, it can be updated with the help of t. The neighbor of node 5 is node 6. C[5][6]=17 Updated The set is as shown below: 17 Find the node with the smallest lowcost, corresponding to t=6, and the selected edges and nodes are as shown below. 18 Add to set U. Add node t to the set U, U={1,2,3,4,5,6,7}, and update V-U={} 19 at the same time. For each adjacent point j of t in the set V-U, it can be updated with the help of t. Node 6 has no adjacent points in the set V-U. No need to update closest[] and lowcost[]. 20 The obtained minimum spanning tree is as follows. The sum of the weights of the minimum spanning tree is 57. Recommended study: " java video tutorial》 The above is the detailed content of The principle and implementation of Prime algorithm in Java (summary sharing). For more information, please follow other related articles on the PHP Chinese website!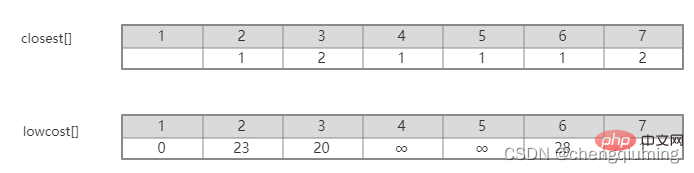
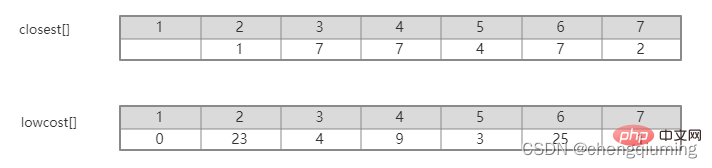
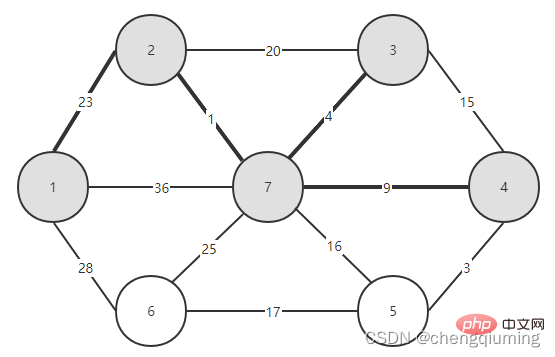 ##14 Find the node with the smallest lowcost, and the corresponding t= 5. The selected edges and nodes are as shown below.
##14 Find the node with the smallest lowcost, and the corresponding t= 5. The selected edges and nodes are as shown below. 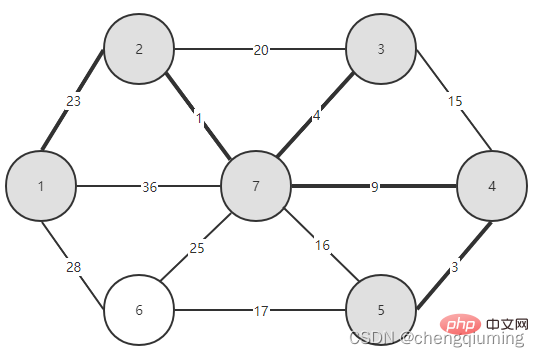 15 Add to set U. Add node t to the set U, U={1,2,3,4,5,7}, and update V-U={6}
15 Add to set U. Add node t to the set U, U={1,2,3,4,5,7}, and update V-U={6}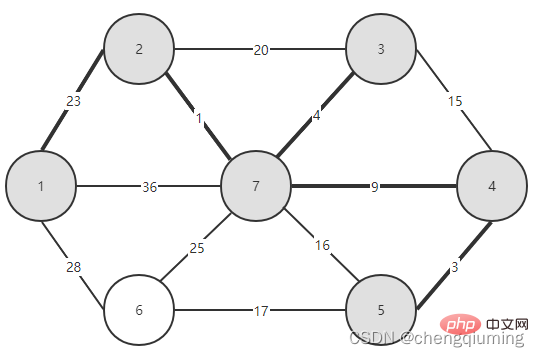
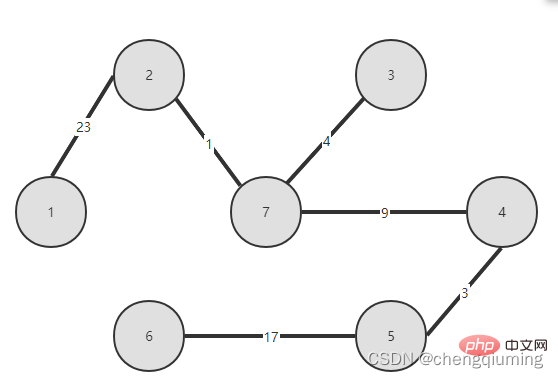
Prime algorithm implementation
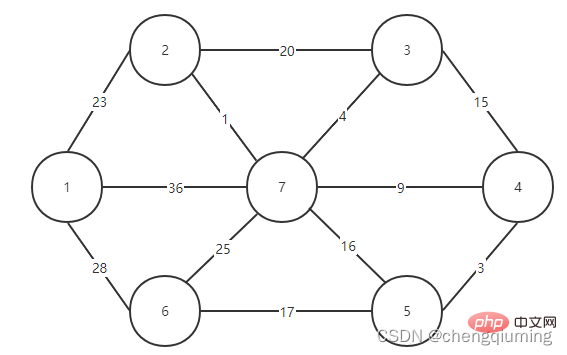
1. The constructed graph
2. Code
package graph.prim;
import java.util.Scanner;
public class Prim {
static final int INF = 0x3f3f3f3f;
static final int N = 100;
// 如果s[i]=true,说明顶点i已加入U
static boolean s[] = new boolean[N];
static int c[][] = new int[N][N];
static int closest[] = new int[N];
static int lowcost[] = new int[N];
static void Prim(int n) {
// 初始时,集合中 U 只有一个元素,即顶点 1
s[1] = true;
for (int i = 1; i <= n; i++) {
if (i != 1) {
lowcost[i] = c[1][i];
closest[i] = 1;
s[i] = false;
} else
lowcost[i] = 0;
}
for (int i = 1; i < n; i++) {
int temp = INF;
int t = 1;
// 在集合中 V-u 中寻找距离集合U最近的顶点t
for (int j = 1; j <= n; j++) {
if (!s[j] && lowcost[j] < temp) {
t = j;
temp = lowcost[j];
}
}
if (t == 1)
break; // 找不到 t,跳出循环
s[t] = true; // 否则,t 加入集合U
for (int j = 1; j <= n; j++) { // 更新 lowcost 和 closest
if (!s[j] && c[t][j] < lowcost[j]) {
lowcost[j] = c[t][j];
closest[j] = t;
}
}
}
}
public static void main(String[] args) {
int n, m, u, v, w;
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
m = scanner.nextInt();
int sumcost = 0;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
c[i][j] = INF;
for (int i = 1; i <= m; i++) {
u = scanner.nextInt();
v = scanner.nextInt();
w = scanner.nextInt();
c[u][v] = c[v][u] = w;
}
Prim(n);
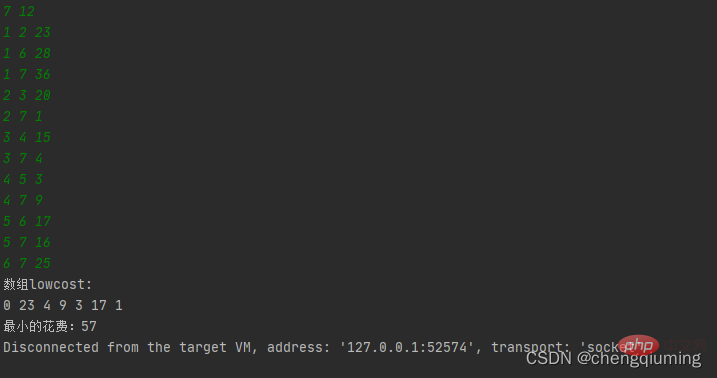
System.out.println("数组lowcost:");
for (int i = 1; i <= n; i++)
System.out.print(lowcost[i] + " ");
System.out.println();
for (int i = 1; i <= n; i++)
sumcost += lowcost[i];
System.out.println("最小的花费:" + sumcost);
}
}3. Test

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1378
1378
 52
52
 Perfect Number in Java
Aug 30, 2024 pm 04:28 PM
Perfect Number in Java
Aug 30, 2024 pm 04:28 PM
Guide to Perfect Number in Java. Here we discuss the Definition, How to check Perfect number in Java?, examples with code implementation.
 Random Number Generator in Java
Aug 30, 2024 pm 04:27 PM
Random Number Generator in Java
Aug 30, 2024 pm 04:27 PM
Guide to Random Number Generator in Java. Here we discuss Functions in Java with examples and two different Generators with ther examples.
 Weka in Java
Aug 30, 2024 pm 04:28 PM
Weka in Java
Aug 30, 2024 pm 04:28 PM
Guide to Weka in Java. Here we discuss the Introduction, how to use weka java, the type of platform, and advantages with examples.
 Smith Number in Java
Aug 30, 2024 pm 04:28 PM
Smith Number in Java
Aug 30, 2024 pm 04:28 PM
Guide to Smith Number in Java. Here we discuss the Definition, How to check smith number in Java? example with code implementation.
 Java Spring Interview Questions
Aug 30, 2024 pm 04:29 PM
Java Spring Interview Questions
Aug 30, 2024 pm 04:29 PM
In this article, we have kept the most asked Java Spring Interview Questions with their detailed answers. So that you can crack the interview.
 Break or return from Java 8 stream forEach?
Feb 07, 2025 pm 12:09 PM
Break or return from Java 8 stream forEach?
Feb 07, 2025 pm 12:09 PM
Java 8 introduces the Stream API, providing a powerful and expressive way to process data collections. However, a common question when using Stream is: How to break or return from a forEach operation? Traditional loops allow for early interruption or return, but Stream's forEach method does not directly support this method. This article will explain the reasons and explore alternative methods for implementing premature termination in Stream processing systems. Further reading: Java Stream API improvements Understand Stream forEach The forEach method is a terminal operation that performs one operation on each element in the Stream. Its design intention is
 TimeStamp to Date in Java
Aug 30, 2024 pm 04:28 PM
TimeStamp to Date in Java
Aug 30, 2024 pm 04:28 PM
Guide to TimeStamp to Date in Java. Here we also discuss the introduction and how to convert timestamp to date in java along with examples.
 Java Program to Find the Volume of Capsule
Feb 07, 2025 am 11:37 AM
Java Program to Find the Volume of Capsule
Feb 07, 2025 am 11:37 AM
Capsules are three-dimensional geometric figures, composed of a cylinder and a hemisphere at both ends. The volume of the capsule can be calculated by adding the volume of the cylinder and the volume of the hemisphere at both ends. This tutorial will discuss how to calculate the volume of a given capsule in Java using different methods. Capsule volume formula The formula for capsule volume is as follows: Capsule volume = Cylindrical volume Volume Two hemisphere volume in, r: The radius of the hemisphere. h: The height of the cylinder (excluding the hemisphere). Example 1 enter Radius = 5 units Height = 10 units Output Volume = 1570.8 cubic units explain Calculate volume using formula: Volume = π × r2 × h (4



