
This article brings you relevant knowledge about java. The dichotomy method is a very efficient algorithm, which is often used in the computer search process. The following will explain the basic idea and implementation of the dichotomy in detail through examples. I hope it will be helpful to everyone.

Recommended study: "java video tutorial"

Idea:
Code
class Solution {
public int search(int[] arr, int t) {
if (arr == null || arr.length < 1) {
return -1;
}
int l = 0;
int r = arr.length - 1;
while (l <= r) {
int m = l + ((r - l) >> 1);
if (arr[m] == t) {
return m;
} else if (arr[m] > t) {
r = m - 1;
} else {
l = m + 1;
}
}
return -1;
}
}Time complexity O(logN).
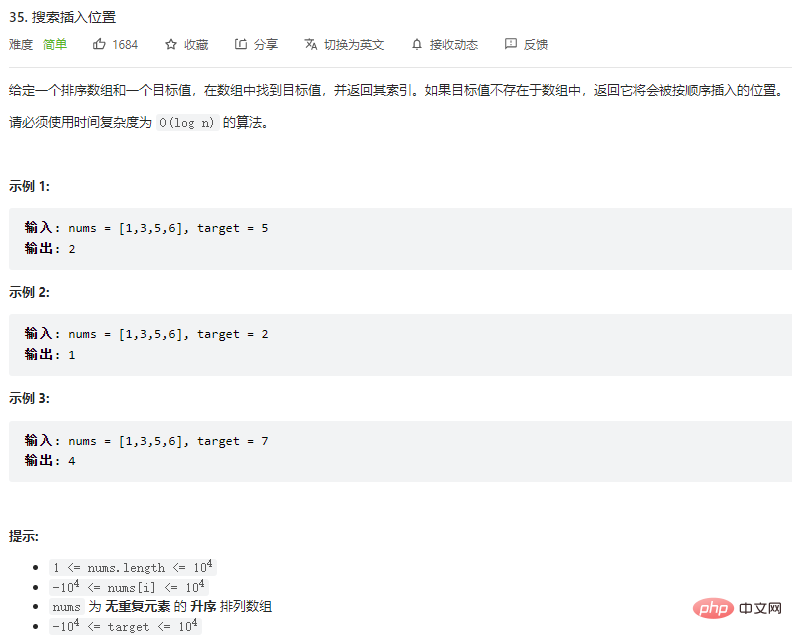
Example 1:
Input: nums = [1,3,5,6], target = 5
Output: 2
Explanation: If you want to insert the element 5 into the array num, It should be inserted between element 3 and element 5, that is, position 2.
Example 2:
Input: nums = [1,3,5,6], target = 2
Output: 1
Explanation: If To insert element 2 into the array num, it should be inserted at the position between element 1 and element 3, that is, position 1.
Example 3:
Input: nums = [1,3,5,6], target = 7
Output: 4
Explanation: If To insert the element 7 into the array num, it should be inserted at the end of the array, that is, at position 4.
As you can know from the above example, this question is essentially askingIn an ordered array, find the leftmost position that is greater than or equal to a certain number. If it does not exist, return the length of the array (representing Insert at the end position)
We only need to make simple changes based on the above example. In the above example, if we find the position that meets the conditions, we can directly return
if (arr[m] == t) {
return m;
}In this question, because we need to find the leftmost position, when encounters equality, we only need to record the position first, without returning directly, and then continue to search on the left Is there any position further to the left that meets the conditions?
At the same time, when encountering arr[m] > t, you also need to record the m position at this time, because this may also is a location that satisfies the conditions.
Code:
class Solution {
public static int searchInsert(int[] arr, int t) {
int ans = arr.length;
int l = 0;
int r = arr.length - 1;
while (l <= r) {
int m = l + ((r - l)>>1);
if (arr[m] >= t) {
ans = m;
r = m - 1;
} else {
l = m + 1;
}
}
return ans;
}
}The time complexity of the entire algorithm is O(logN).
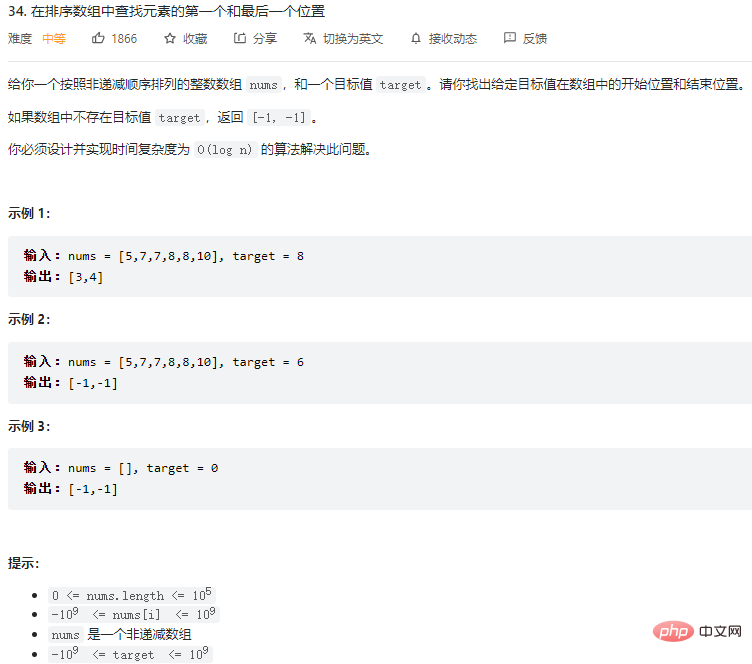
Ideas
This question is also solved using binary division. When an element is found through binary division, do not rush back, but continue to search to the left (right) to see if you can find a matching value further to the left (right).
The code is as follows:
class Solution {
public static int[] searchRange(int[] arr, int t) {
if (arr == null || arr.length < 1) {
return new int[]{-1, -1};
}
return new int[]{left(arr,t),right(arr,t)};
}
public static int left(int[] arr, int t) {
if (arr == null || arr.length < 1) {
return -1;
}
int ans = -1;
int l = 0;
int r = arr.length - 1;
while (l <= r) {
int m = l + ((r - l) >> 1);
if (arr[m] == t) {
ans = m;
r = m - 1;
} else if (arr[m] < t) {
l = m +1;
} else {
// arr[m] > t
r = m - 1;
}
}
return ans;
}
public static int right(int[] arr, int t) {
if (arr == null || arr.length < 1) {
return -1;
}
int ans = -1;
int l = 0;
int r = arr.length - 1;
while (l <= r) {
int m = l + ((r - l) >> 1);
if (arr[m] == t) {
ans = m;
l = m + 1;
} else if (arr[m] < t) {
l = m +1;
} else {
// arr[m] > t
r = m - 1;
}
}
return ans;
}
}Time complexity O(logN).

Idea
Assume that the length of the array is N, first determine 0 Are the number at position and the number at position N-1 the peak position? The
0 position only needs to be compared with the 1 position. If the 0 position is larger, the 0 position It is the peak position and can be returned directly. The
N-1 position only needs to be compared with the N-2 position. If the N-1 position is larger, Position N-1 is the peak position and can be returned directly.
If the 0 position and N-1 are both minimum values in the last round of comparison, then the array must look like the following:

As can be seen from the above figure, the [0..1] interval is a growth trend, [N-2...N-1] Within the range is a downward trend.
Then the peak position must appear between [1...N-2].
At this time, you can find the peak position by bisection, first go to the midpoint position, assuming it is mid, if the value of the midpoint position is greater than the value of the left and right sides Duda:
arr[mid] > arr[mid+1] && arr[mid] > arr[mid-1]
then the mid position is the peak position and returns directly.
Otherwise, there are two situations as follows:
Case 1: The value of mid position is smaller than the value of mid - 1 position
趋势如下图:

则在[1...(mid-1)]区间内继续二分。
情况二:mid 位置的值比 mid + 1 位置的值小
趋势是:

则在[(mid+1)...(N-2)]区间内继续上述二分。
完整代码
public class LeetCode_0162_FindPeakElement {
public static int findPeakElement(int[] nums) {
if (nums.length == 1) {
return 0;
}
int l = 0;
int r = nums.length - 1;
if (nums[l] > nums[l + 1]) {
return l;
}
if (nums[r] > nums[r - 1]) {
return r;
}
l = l + 1;
r = r - 1;
while (l <= r) {
int mid = l + ((r - l) >> 1);
if (nums[mid] > nums[mid + 1] && nums[mid] > nums[mid - 1]) {
return mid;
}
if (nums[mid] < nums[mid + 1]) {
l = mid + 1;
} else if (nums[mid] < nums[mid - 1]) {
r = mid - 1;
}
}
return -1;
}
}时间复杂度O(logN)。
推荐学习:《java视频教程》
The above is the detailed content of Briefly understand the basic ideas and implementation of dichotomy in Java. For more information, please follow other related articles on the PHP Chinese website!
![JavaScript core tutorial [DOM BOM operations that JS must know]](https://img.php.cn/upload/course/000/000/041/61c56ae28d02a390.jpg)
![Practical development of imitation Meituan APP [A must-have JavaScript project for front-end programmers]](https://img.php.cn/upload/course/000/000/068/6242bebc05ca9210.png)


