To solve the problem of VAE representation learning, Hokkaido University proposed a new generative model GWAE

Learning low-dimensional representations of high-dimensional data is a fundamental task in unsupervised learning because such representations succinctly capture the essence of the data and enable execution based on low-dimensional inputs downstream tasks are possible. Variational autoencoder (VAE) is an important representation learning method, however due to its objective control representation learning is still a challenging task. Although the evidence lower bound (ELBO) goal of VAE is generatively modeled, learning representations is not directly targeted at this goal, which requires specific modifications to the representation learning task, such as disentanglement. These modifications sometimes lead to implicit and undesirable changes in the model, making controlled representation learning a challenging task.

To solve the representation learning problem in variational autoencoders, this paper proposes a new generative model called Gromov-Wasserstein Autoencoders (GWAE). GWAE provides a new framework for representation learning based on the variational autoencoder (VAE) model architecture. Unlike traditional VAE-based representation learning methods for generative modeling of data variables, GWAE obtains beneficial representations through optimal transfer between data and latent variables. The Gromov-Wasserstein (GW) metric makes possible such optimal transfer between incomparable variables (e.g. variables with different dimensions), which focuses on the distance structure of the variables under consideration. By replacing the ELBO objective with the GW metric, GWAE performs a comparison between the data and the latent space, directly targeting representation learning in variational autoencoders (Figure 1). This formulation of representation learning allows the learned representations to have specific properties that are considered beneficial (e.g., decomposability), which are called meta-priors.

##Figure 1 The difference between VAE and GWAE

This study has so far Accepted by ICLR 2023.

• Paper link: https://arxiv.org/abs/2209.07007
##​
• Code link: https://github.com/ganmodokix/gwae
Method introduction

Between data distribution and potential prior distribution The GW target is defined as follows:

This formula of optimal transmission cost can measure the inconsistency of distribution in incomparable space; however, for continuous distribution , it is impractical to calculate exact GW values ​​due to the need to lower bound all couplings. To solve this problem, GWAE solves a relaxed optimization problem to estimate and minimize the GW estimator, the gradient of which can be calculated by automatic differentiation. The relaxation target is the sum of the estimated GW metric and three regularization losses, which can all be implemented in a differentiable programming framework such as PyTorch. This relaxation objective consists of a main loss and three regularization losses, namely the main estimated GW loss, the WAE-based reconstruction loss, the merged sufficient condition loss, and the entropy regularization loss.

This scheme can also flexibly customize the prior distribution to introduce beneficial features into the low-dimensional representation. Specifically, the paper introduces three prior populations, which are:

Neural Priori (NP) In GWAEs with NP, a fully connected neural network is used to construct a priori sampler. This family of prior distributions makes fewer assumptions about the underlying variables and is suitable for general situations.

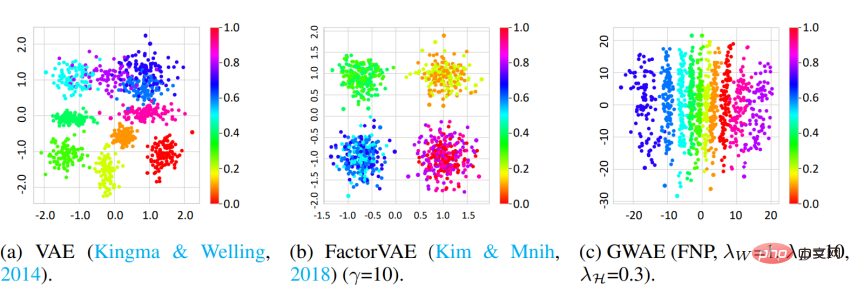
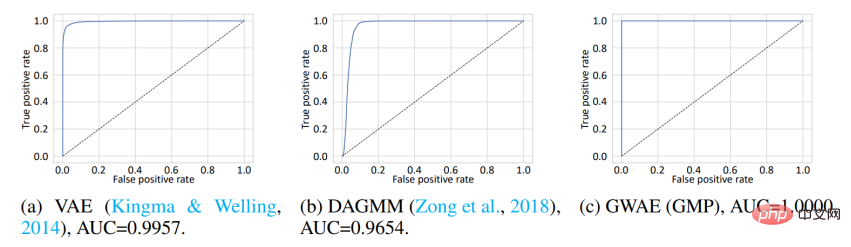
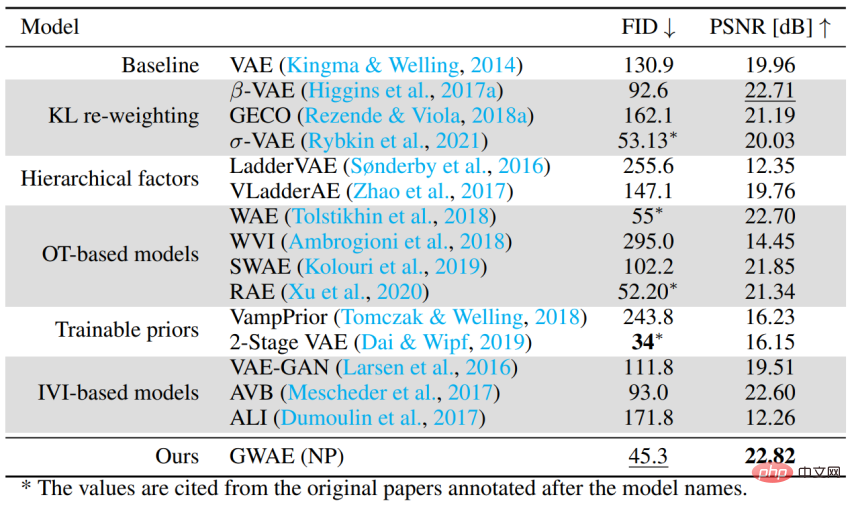
Factorized Neural Priors (FNP)In GWAEs with FNP, use locally connected neural priors The network builds a sampler in which entries for each latent variable are generated independently. This sampler produces a factorized prior and a term-independent representation, which is a prominent method for representative meta-prior,disentanglement.

Gaussian Mixture Prior (GMP) In GMP, it is defined as a mixture of several Gaussian distributions, and its sampler can use heavy Parameterization techniques and Gumbel-Max techniques are implemented. GMP allows clusters to be hypothesized in the representation, where each Gaussian component of the prior is expected to capture a cluster.

Experiments and results

This study conducted two main meta-prior empirical evaluations of GWAE:Solution Entanglement and clustering.

Disentanglement The study used the 3D Shapes dataset and DCI metric to measure the disentanglement ability of GWAE. The results show that GWAE using FNP is able to learn object hue factors on a single axis, which demonstrates the disentanglement capability of GWAE. Quantitative evaluation also demonstrates the disentanglement performance of GWAE.

Clustering To evaluate the representations obtained based on clustering element priors, the study conducted a Out-of-Distribution (OoD) detection. The MNIST dataset is used as In-Distribution (ID) data and the Omniglot dataset is used as OoD data. While MNIST contains handwritten numbers, Omniglot contains handwritten letters with different letters. In this experiment, the ID and OoD datasets share the domain of handwritten images, but they contain different characters. Models are trained on ID data and then use their learned representations to detect ID or OoD data. In VAE and DAGMM, the variable used for OoD detection is the prior log-likelihood, while in GWAE it is the Kantorovich potential. The prior for GWAE was constructed using GMP to capture the clusters of MNIST. The ROC curve shows the OoD detection performance of the models, with all three models achieving near-perfect performance; however, the GWAE built using GMP performed best in terms of area under the curve (AUC).

In addition, this study evaluated the generative ability of GWAE.

Performance as an Autoencoder-Based Generative Model To evaluate the ability of GWAE to handle the general case without specific meta-priors, the CelebA data is used The set generation performance was evaluated. The experiment uses FID to evaluate the model's generative performance and PSNR to evaluate the autoencoding performance. GWAE achieved the second best generative performance and the best autoencoding performance using NP, demonstrating its ability to capture the data distribution in its model and capture the data information in its representation.

Summary

• GWAE is a variational autoencoder generative model built based on the Gromov-Wasserstein metric, aiming to Direct representation learning.
• Since the prior only requires differentiable samples, various prior distribution settings can be constructed to assume meta-priors (ideal properties of the representation).
• Experiments on primary meta-priors and performance evaluation as a variational autoencoder demonstrate the flexibility of the GWAE formulation and the representation learning capabilities of GWAE.
• First author Nao Nakagawa’s personal homepage: https://ganmodokix.com/note/cv
• Hokkaido University Multimedia Laboratory homepage: https://www-lmd.ist.hokudai.ac.jp/

The above is the detailed content of To solve the problem of VAE representation learning, Hokkaido University proposed a new generative model GWAE. For more information, please follow other related articles on the PHP Chinese website!