Google and Stanford jointly issued an article: Why must we use large models?

​Language models have profoundly changed the research and practice in the field of natural language processing. In recent years, large models have made important breakthroughs in many fields. They do not need to be fine-tuned on downstream tasks. With appropriate instructions or prompts, they can achieve excellent performance, sometimes even amazing.

For example, GPT-3 [1] can write love letters, scripts, and solve complex mathematical reasoning problems with data, and PaLM [2] can interpret jokes. The above example is just the tip of the iceberg of large model capabilities. Many applications have been developed using large model capabilities. You can see many related demos on the OpenAI website [3], but these capabilities are rarely reflected in small models.

In the paper introduced today, the capabilities that small models do not have but large models have are called emergent capabilities (Emergent Abilities), which means that the scale of the model is large enough to a certain extent. A sudden ability acquired later. This is a process in which quantitative changes produce qualitative changes.

The emergence of emergent capabilities is difficult to predict. Why the model suddenly acquires certain capabilities as the scale increases is still an open question that requires further research to answer. In this article, the author sorts out some recent progress in understanding large models and gives some related thoughts. I look forward to discussing it with you.

Related papers:​

• Emergent Abilities of Large Language Models.
  http://arxiv. org/abs/2206.07682
• Beyond the Imitation Game: Quantifying and extrapolating the capabilities of language models.
  https://arxiv.org/abs/ 2206.04615

The emergent ability of large models

What is a large model? What size is considered "big"? This doesn't have a clear definition.

Generally speaking, model parameters may have to reach one billion levels before they show capabilities that are significantly different from the zero-shot and few-shot capabilities of small models. In recent years, there have been multiple models with hundreds of billions and trillions of parameters, which have achieved SOTA performance on a series of tasks. In some tasks, the model's performance improves reliably with increasing scale, while in other tasks, the model shows a sudden increase in performance at a certain scale. Two indicators can be used to classify different tasks [4]: ​​

• Linearity: aims to measure the extent to which the model performs on the task as the scale increases have been reliably improved.

• Breakthroughness: Aims to measure how well a task can be learned when the model size exceeds a critical value.

These two indicators are functions of model size and model performance. For specific calculation details, please refer to [4]. The figure below shows some examples of high Linearity and high Breakthroughness tasks.

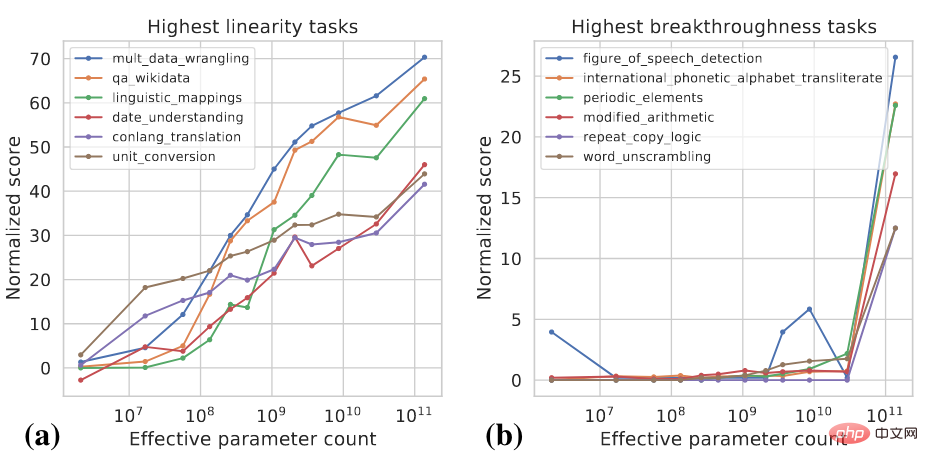
High linearity tasks are mostly knowledge-based, which means they mainly rely on memorizing the knowledge that exists in the training data. Information, such as answering factual questions. Larger models usually use more data for training and can remember more knowledge, so the model shows steady improvement in such tasks as the scale increases. High-breakthroughness tasks include more complex tasks that require the use of several different abilities or the execution of multiple steps to arrive at the correct answer, such as mathematical reasoning. Smaller models struggle to acquire all the capabilities needed to perform such tasks.

The following figure further shows the performance of different models on some high-breakthroughness tasks

​

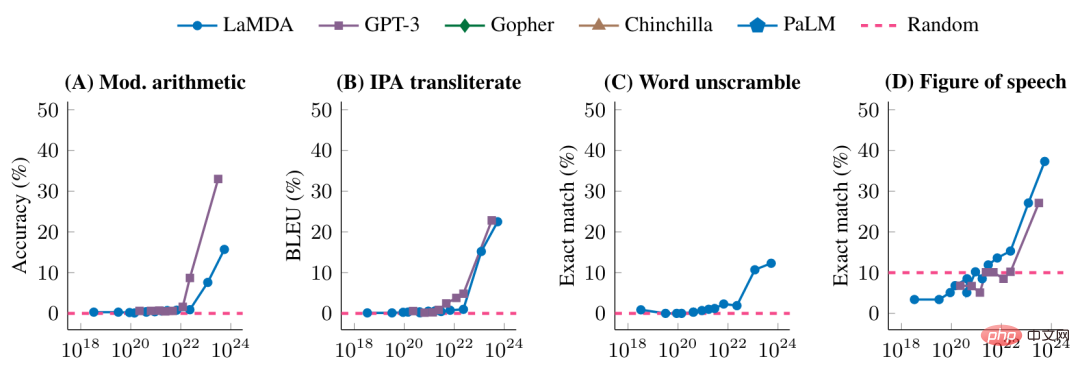
Before reaching a certain model scale, the model's performance on these tasks is random. After reaching a certain scale, there is a significant improvement.

Is it smooth or sudden?

What we saw earlier is that the model suddenly gained certain capabilities after the scale increased to a certain level. From the perspective of task-specific indicators, these capabilities are emergent, but from another perspective, the potential changes in model capabilities Smoother. This article discusses the following two perspectives: (1) using smoother indicators; (2) decomposing complex tasks into multiple subtasks.

The following figure (a) shows the change curve of the log probability of the real target for some high breakthroughness tasks. The log probability of the real target gradually increases as the model size increases.

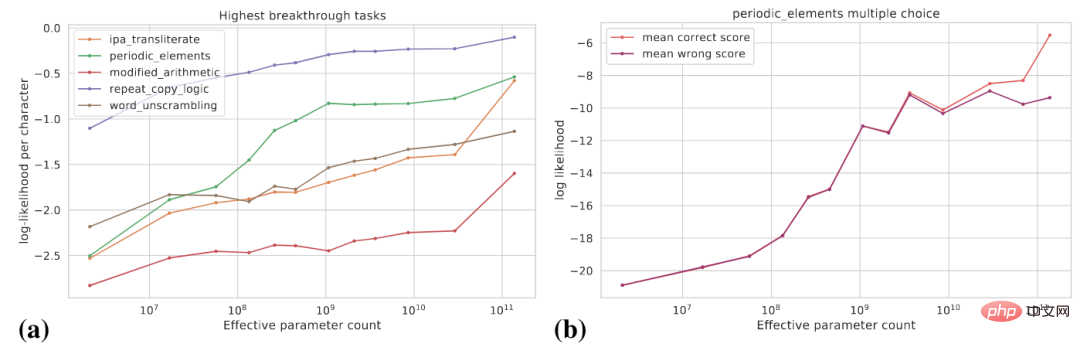
Figure (b) shows that for a certain multiple-choice task, as the model size increases, The log probability of a correct answer increases gradually, while the log probability of an incorrect answer increases gradually up to a certain size and then levels off. After this scale, the gap between the probability of correct answers and the probability of wrong answers widens, and the model achieves significant performance improvements.

In addition, for a specific task, suppose we can use Exact Match and BLEU to evaluate the performance of the model. BLEU is a smoother indicator than Exact Match, and different indicators are used. There may be significant differences in the trends seen.

For some tasks, the model may gain partial ability to do this task at different scales. The picture below is the task of guessing the name of a movie through a string of emoji

We can see that the model starts to guess at some scales Movie Titles, Recognizing the Semantics of Emojis at a Larger Scale, Producing Correct Answers at the Largest Scale.

Large models are sensitive to how tasks are formalized

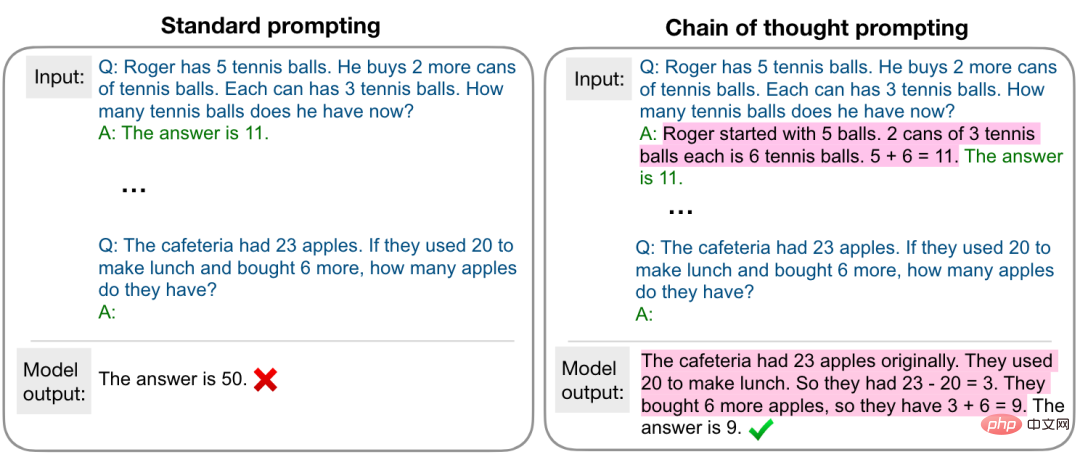
The scale at which a model shows a sudden improvement in capabilities also depends on how the tasks are formalized. For example, on complex mathematical reasoning tasks, if standard prompting is used to treat it as a question and answer task, the performance improvement will be very limited as the model size is increased. However, if chain-of-thought prompting [5] is used as shown in the figure below, it will be treated as a question and answer task. Treated as a multi-step inference task, significant performance improvements will be seen at a certain scale.

##What’s more, researchers found that by adding a simple prompt "Let's think step by step" can greatly improve GPT-3's zero-shot reasoning ability [6], as shown in the figure below

What this inspires us is that sometimes a large model cannot do a certain task well. It may not be that it really cannot do it well, but that it needs a suitable way to stimulate its ability.

Is the bigger the model necessarily the stronger?

The previous discussion gives us an intuitive feeling that the performance must be improved as the model size increases, but is this really the case? In fact, for some tasks, the performance may actually decrease as the model becomes larger, as shown in the figure below

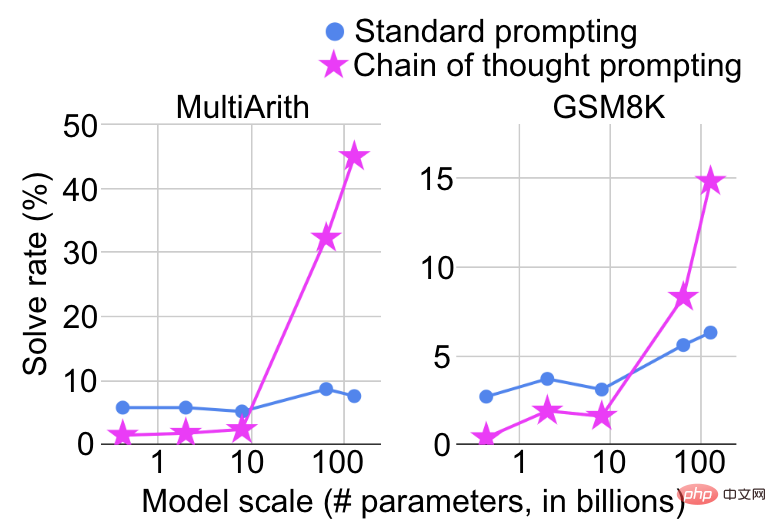
## Several researchers at New York University also organized a competition to find tasks where models perform worse as they get larger.

#For example, in a question and answer task, if you add your beliefs along with the question, the large model will be more easily affected. Interested students can pay attention.

Summary and Thoughts

• In most tasks, as the size of the model increases, the performance of the model becomes better. , but there will also be some counterexamples. More research is needed to better understand the behavior of models.

• #The ability of large models needs to be stimulated in appropriate ways.

• #Is the large model really doing inference? As we have seen before, by adding the prompt “Let’s think step by step”, the large model can perform multi-step reasoning and achieve satisfactory results on mathematical reasoning tasks. It seems that the model already possesses human reasoning capabilities. However, as shown below, if you give GPT-3 a meaningless question and let it do multi-step reasoning, GPT-3 seems to be doing reasoning, but in fact it is some meaningless output. As the saying goes "garbage in, garbage out". In comparison, humans can judge whether the question is reasonable, that is, whether the current question is answerable under given conditions. "Let's think step by step" can work. I think the fundamental reason is that GPT-3 has seen a lot of similar data during the training process. What it does is just predict the next token based on the previous token. Unlike humans, There are still fundamental differences in the way of thinking. Of course, if appropriate prompts are given to GPT-3 to determine whether the question is reasonable, it may be able to do so to some extent, but I am afraid there is still a considerable distance between "thinking" and "reasoning". This is not a simple matter. This can be solved by increasing the size of the model. Models may not need to think like humans, but more research is urgently needed to explore paths other than increasing model size.

• System 1 or System 2? The human brain has two systems that cooperate with each other. System 1 (intuition) is fast and automatic, while System 2 (rationality) is slow and controllable. A large number of experiments have proven that people prefer to use intuition to make judgments and decisions, and rationality can correct the biases caused by it. Most current models are designed based on System 1 or System 2. Can future models be designed based on dual systems?

• #Query language in the era of large models. Previously, we stored knowledge and data in databases and knowledge graphs. We can use SQL to query relational databases, and SPARQL to query knowledge graphs. So what query language do we use to call the knowledge and capabilities of large models?

Mr. Mei Yiqi once said, "The so-called great scholar does not mean a building, but a master." The author uses an inappropriate term here. Let’s end this article with an analogy: the so-called large model does not mean that it has parameters, but that it has capabilities. ​

The above is the detailed content of Google and Stanford jointly issued an article: Why must we use large models?. For more information, please follow other related articles on the PHP Chinese website!