 Technology peripherals
Technology peripherals
 AI
AI
 Is the equation a binary tree forest? Discover unknown governing equations and physical mechanisms directly from data
Is the equation a binary tree forest? Discover unknown governing equations and physical mechanisms directly from data
Is the equation a binary tree forest? Discover unknown governing equations and physical mechanisms directly from data
Researchers hope to use machine learning methods to automatically mine the most valuable and important intrinsic laws directly from high-dimensional nonlinear data (that is, to mine the PDE-based governing equations behind the problem) to achieve automatic knowledge discovery.
Recently, research teams from Eastern Institute of Technology, University of Washington, Ruilai Intelligence, and Peking University have proposed a genetic algorithm SGA-PDE based on symbolic mathematics, constructing an open candidate set that can extract data from data. Directly mine arbitrary forms of governing equations.
Experiments show that SGA-PDE can not only mine the Burgers equation (with interaction terms), the Korteweg–de Vries equation (KdV, with higher-order derivative terms), and the Chafee-Infante equation (with exponential terms) from the data terms and derivative terms), and also successfully mined the governing equations with composite functions and equations with fractional structures in the viscous gravity flow problem, the latter two of which were difficult to discover with previous methods. SGA-PDE does not rely on prior knowledge about the equation form and fills the gap in complex structure control equation mining problems. This model does not require a candidate set of equations to be given in advance, which is beneficial to the practical application of automatic knowledge discovery algorithms in unknown scientific problems.
The study was titled "Symbolic genetic algorithm for discovering open-form partial differential equations (SGA-PDE)" and was published in Physical Review Research on June 1.

The current common knowledge discovery idea is to use sparse regression, that is, pre-given a closed candidate set, then select equation terms from it, and combine the governing equations, such as SINDy and PDE-FIND. However, this type of method requires the user to determine the rough form of the equation in advance, and then provide all corresponding differential operators as function terms in the candidate set in advance. It is impossible to find function terms that do not exist in the candidate set from the data . Some of the latest research attempts to use genetic algorithms to expand the candidate set, but there are major limitations in gene recombination and mutation, and it is still unable to generate complex structural function terms (such as fractional structures and composite functions)
The key to mining open-form governing equations directly from data is to generate and represent arbitrary forms of governing equations in a way that is easy to compute, and to evaluate the accuracy of the equation form by measuring how well the generated equations fit the observed data. properties, and then iteratively optimize the mined equations. Therefore, the core issues of automatic knowledge discovery are representation and optimization.
Table 1. Comparison table of automatic control equation mining methods
The challenge of expressing the problem is:1. How to use Limited basic units to represent infinite complex structural control equations (i.e., open candidate sets);2. How to construct an easy-to-compute control equation representation method. In order to freely express equations of any structure, the researchers weakened the basic representation unit of SGA-PDE to operands and operators, and used symbolic mathematics to construct an open candidate set using binary trees.
The challenges of the optimization problem are:1. The gradient between the equation form and the equation evaluation index is difficult to calculate; 2. The feasible domain of the open candidate set is infinite, and the optimization process It is difficult to effectively balance exploration and exploitation. In order to efficiently optimize the open candidate set problem, the researchers used a genetic algorithm specially designed for tree structures to achieve optimization in the form of equations.
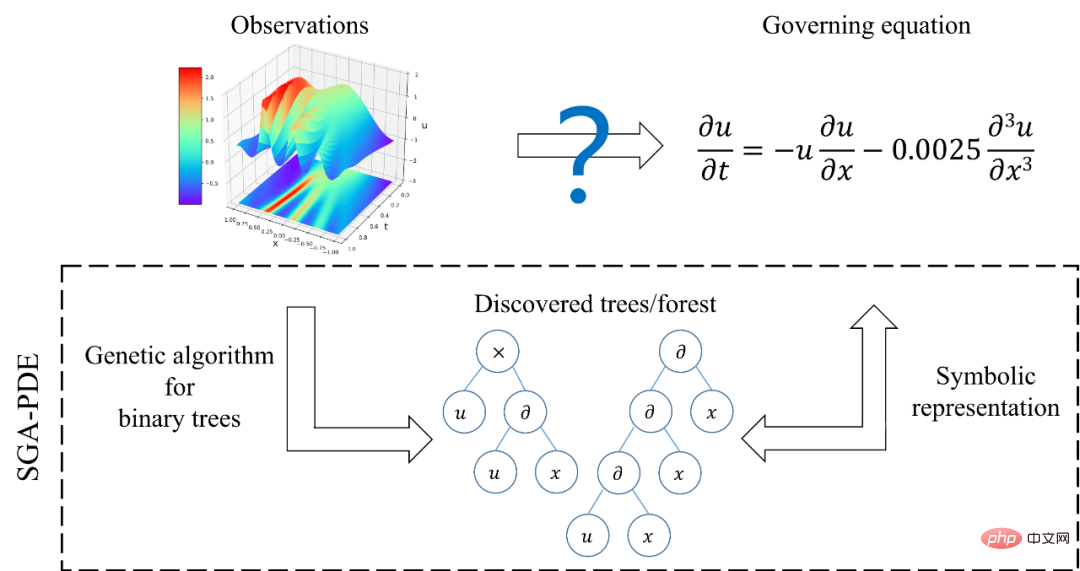
Figure 1: Schematic diagram of automatic knowledge discovery problem and SGA-PDE
The researchers first refined the basics of the equations in the algorithm Representation units are used to represent open-form partial differential equations,transforming the representation scale of equations from the level of independent function terms to the more basic level of operators and operands.
SGA-PDE divides the operators in the control equation into double operators (such as, -) and single operators (such as sin, cos), and then defines all potential variables as operands (such as x, t, u ). Researchers use the structure of a binary tree to combine operators and operands to encode different equations. All terminal nodes (leaf nodes with degree 0) in the binary tree correspond to operands, and all non-terminal nodes correspond to operators. Double operators correspond to nodes with degree 2, and single operators correspond to nodes with degree 1. .
As shown in Figure 2, through a computable string as a connection, Any function term can be converted into a binary tree, and at the same time, satisfies certain mathematical rules Binary trees can also be converted into function terms. Furthermore, a governing equation with multiple function terms is equivalent to a forest composed of multiple binary trees. SGA-PDE represents any open-form partial differential governing equation through symbolic mathematics. In addition, the paper also proposes a method to randomly generate binary trees with mathematical meaning, which can ensure that the generated binary trees do not violate mathematical principles.
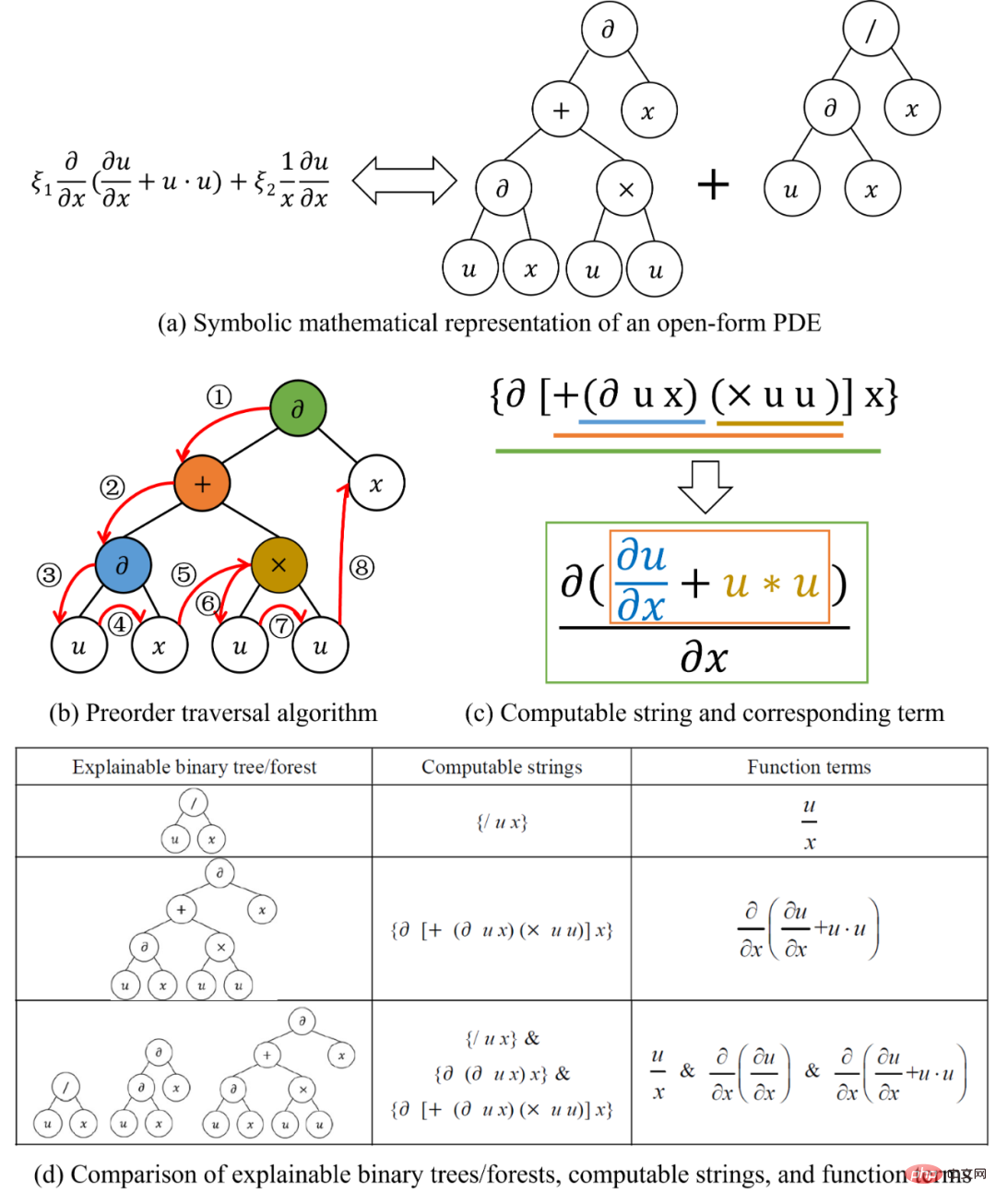
Figure 2: Representation and transformation method between binary tree and function terms
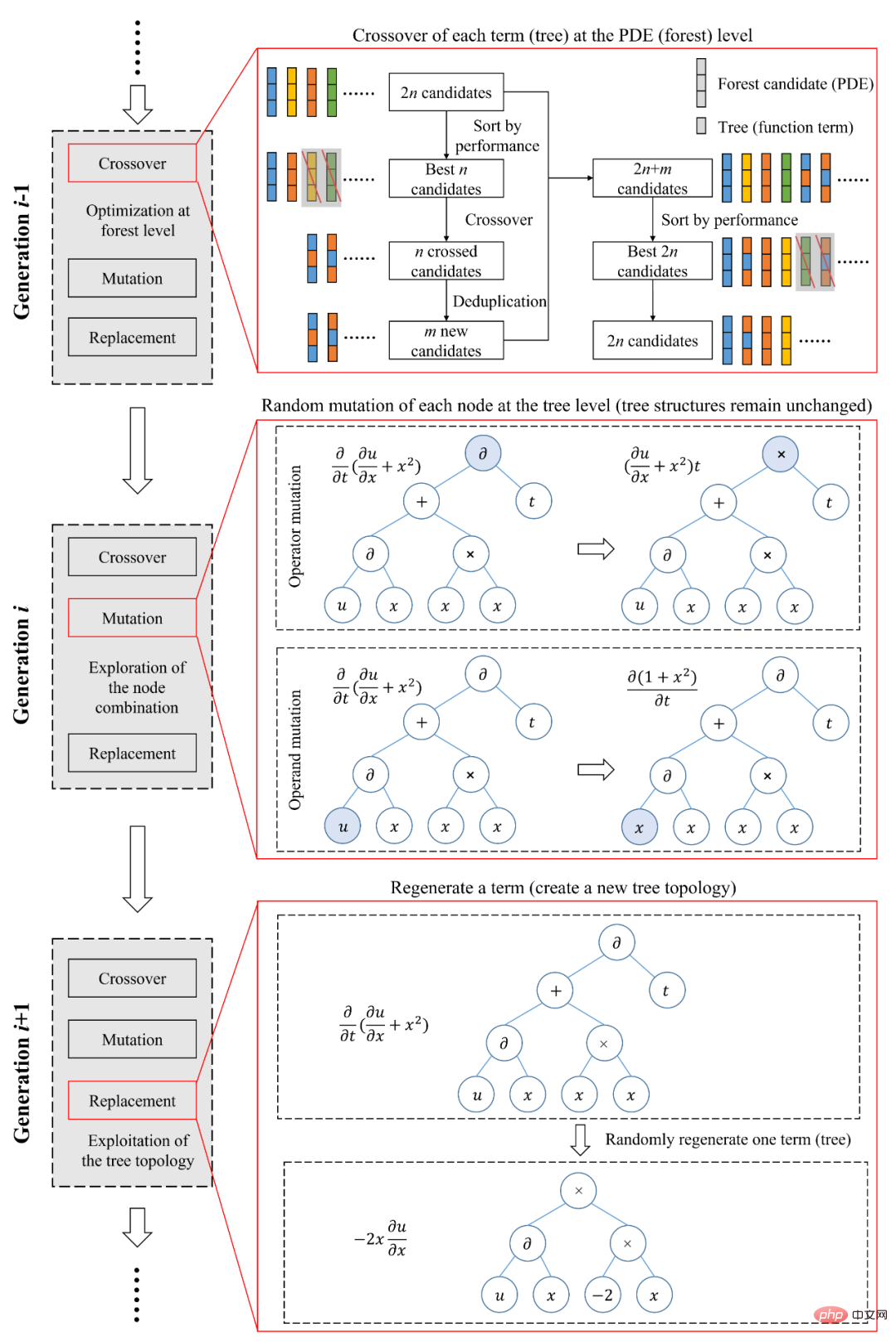
Because the representation method shown in Figure 2 can There is a one-to-one correspondence between samples in the function space and samples in the binary tree space. This means that the representation method based on symbolic mathematics is efficient and non-redundant and can be used as the encoding process in the genetic algorithm. The researchers proposed a genetic algorithm for tree structures (Figure 3) to automatically mine control equations consistent with observed data from experimental data. This genetic algorithm for tree structures can achieve optimization at different levels.
The reorganization link is to optimizeat the forest (equation) level to find the optimal combination of binary trees (function terms). This link is similar to the current common sparse regression method, which is optimization within a closed candidate set.
The mutation link is optimized at the binary tree (function term) level. By randomly generating different node attributes, we find the optimal combination of node attributes under a given binary tree structure. Essentially It is an exploitation of the current structure.
The replacement process is also optimized at the binary tree (function item) level, but it will generate a new binary tree structure, which is an exploration of the tree structure and achieves a completely open candidate set. optimization. SGA-PDE can take into account the utilization and exploration of binary tree topology through multi-level optimization, which is conducive to efficiently finding the optimal equation form.
The experimental data is shown in Figure 4, in which the second column shows Physical field observations,
are the only input informationof SGA-PDE. The underlying first derivatives in columns 3 and 4 can be obtained by differencing the physical field observations. Column 1 is the correct form of the equation. In the experiment, SGA-PDE uses the same preset operands and operators, and does not need to be adjusted for specific problems in order to verify the versatility of the algorithm. Finally, SGA-PDE successfully mined the Burgers equation, KdV equation, Chafee-Infante equation, viscous gravity flow governing equations with composite function derivation, and equations with fractional structure from the data. The above equation has many complex forms
such as exponential terms, higher-order derivative terms, interaction terms, composite functions and nested structures.Table 2 compares the calculation results of various existing algorithms in the above five calculation examples. It can be seen that SGA-PDE fills the gap in mining the control equations of complex structures
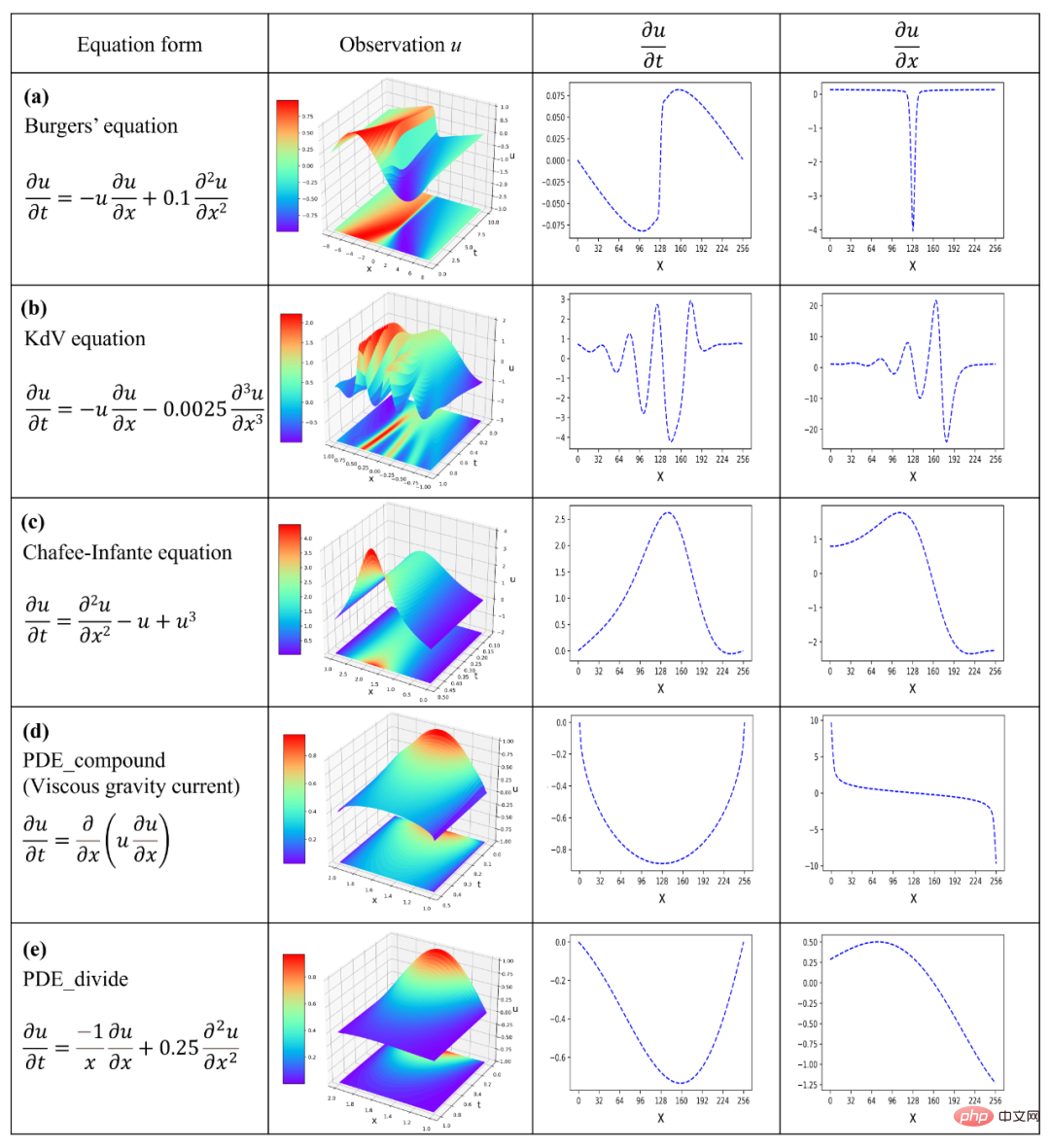 Figure 4: Experimental data graph
Figure 4: Experimental data graph

Table 2 Experimental results of automatic knowledge discovery algorithm in different control equation mining problems
In order to more fully understand the search of SGA-PDE Optimization process, Figure 5 shows the evolution path when mining the KdV equation. It can be seen that the optimal equation generated by the first generation is far from the actual equation. In the subsequent evolution process, with the changes in the topological structure of the binary tree and the meaning of the nodes, as well as the cross-recombination between function terms, the correct solution was finally found in the 31st generation, and at this time the AIC index has reached the convergence given in the article standard. Interestingly, if the optimization is continued, a more parsimonious expression of the KdV equation based on the derivation of a composite function is found at generation 69. Figure 6 shows the optimization process of SGA-PDE to find the governing equations with fractional structure.

Figure 5: SGA-PDE optimization process of KdV equation
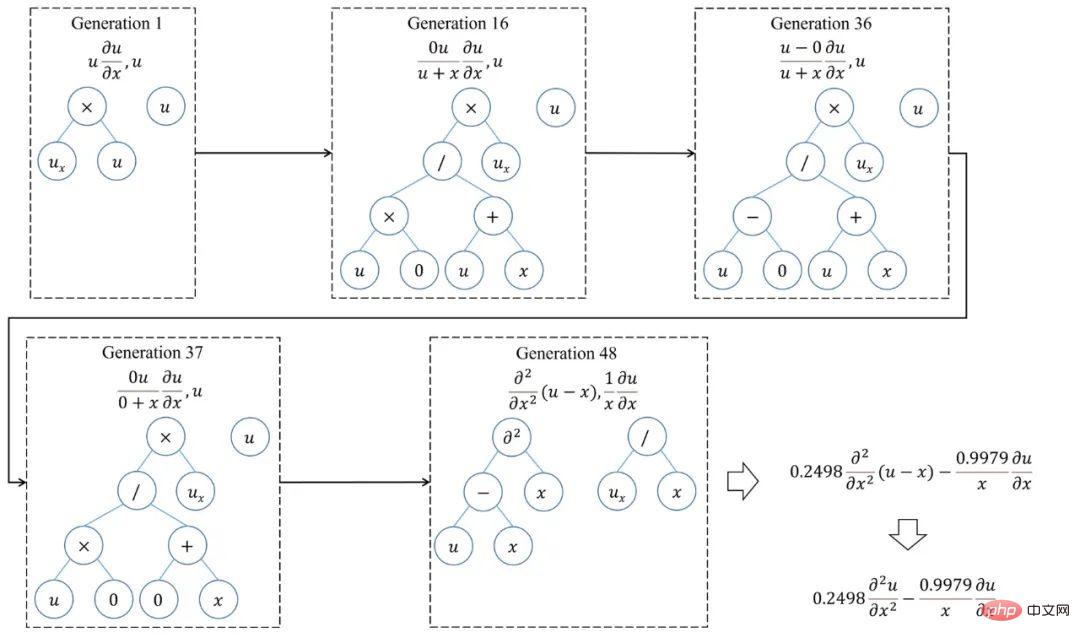
Figure 6: SGA-PDE optimization process for equations with fractional structure
Control equations are an efficient representation of domain knowledge. However, the equation parameters and even equation forms of many real-world problems are Uncertain, it is difficult to write accurate control equations, which greatly restricts the application of domain knowledge in machine learning.
SGA-PDE transforms equations through symbolic mathematics and solves the representation problem of arbitrary forms of partial differential equations. In addition, SGA-PDE uses a genetic algorithm designed for binary trees, and automatically mines control equations consistent with observation data from the open domain through iterative optimization of the tree's topology and node attributes. In optimization, SGA-PDE does not rely on prior information in the form of equations, nor does it need to be given a candidate set, realizing automatic optimization of complex structural equations. At the same time, SGA-PDE is also a gradient-free algorithm, which avoids the problem of difficult calculation of the gradient between the equation structure and the loss value.
Future research will focus on: 1. Try to combine reinforcement learning or combinatorial optimization algorithms; 2. Reduce the solution space by embedding physical mechanisms; 3. Evaluate and improve the applicability of SGA-PDE to sparse data and noisy data. nature; 4. Integrate knowledge embedding methods and knowledge discovery methods.
Paper link (available for free):
https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.4.023174
Code and example data Link:
https://github.com/YuntianChen/SGA-PDE
The above is the detailed content of Is the equation a binary tree forest? Discover unknown governing equations and physical mechanisms directly from data. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1389
1389
 52
52
 Use ddrescue to recover data on Linux
Mar 20, 2024 pm 01:37 PM
Use ddrescue to recover data on Linux
Mar 20, 2024 pm 01:37 PM
DDREASE is a tool for recovering data from file or block devices such as hard drives, SSDs, RAM disks, CDs, DVDs and USB storage devices. It copies data from one block device to another, leaving corrupted data blocks behind and moving only good data blocks. ddreasue is a powerful recovery tool that is fully automated as it does not require any interference during recovery operations. Additionally, thanks to the ddasue map file, it can be stopped and resumed at any time. Other key features of DDREASE are as follows: It does not overwrite recovered data but fills the gaps in case of iterative recovery. However, it can be truncated if the tool is instructed to do so explicitly. Recover data from multiple files or blocks to a single
 Open source! Beyond ZoeDepth! DepthFM: Fast and accurate monocular depth estimation!
Apr 03, 2024 pm 12:04 PM
Open source! Beyond ZoeDepth! DepthFM: Fast and accurate monocular depth estimation!
Apr 03, 2024 pm 12:04 PM
0.What does this article do? We propose DepthFM: a versatile and fast state-of-the-art generative monocular depth estimation model. In addition to traditional depth estimation tasks, DepthFM also demonstrates state-of-the-art capabilities in downstream tasks such as depth inpainting. DepthFM is efficient and can synthesize depth maps within a few inference steps. Let’s read about this work together ~ 1. Paper information title: DepthFM: FastMonocularDepthEstimationwithFlowMatching Author: MingGui, JohannesS.Fischer, UlrichPrestel, PingchuanMa, Dmytr
 How to use Excel filter function with multiple conditions
Feb 26, 2024 am 10:19 AM
How to use Excel filter function with multiple conditions
Feb 26, 2024 am 10:19 AM
If you need to know how to use filtering with multiple criteria in Excel, the following tutorial will guide you through the steps to ensure you can filter and sort your data effectively. Excel's filtering function is very powerful and can help you extract the information you need from large amounts of data. This function can filter data according to the conditions you set and display only the parts that meet the conditions, making data management more efficient. By using the filter function, you can quickly find target data, saving time in finding and organizing data. This function can not only be applied to simple data lists, but can also be filtered based on multiple conditions to help you locate the information you need more accurately. Overall, Excel’s filtering function is a very practical
 Google is ecstatic: JAX performance surpasses Pytorch and TensorFlow! It may become the fastest choice for GPU inference training
Apr 01, 2024 pm 07:46 PM
Google is ecstatic: JAX performance surpasses Pytorch and TensorFlow! It may become the fastest choice for GPU inference training
Apr 01, 2024 pm 07:46 PM
The performance of JAX, promoted by Google, has surpassed that of Pytorch and TensorFlow in recent benchmark tests, ranking first in 7 indicators. And the test was not done on the TPU with the best JAX performance. Although among developers, Pytorch is still more popular than Tensorflow. But in the future, perhaps more large models will be trained and run based on the JAX platform. Models Recently, the Keras team benchmarked three backends (TensorFlow, JAX, PyTorch) with the native PyTorch implementation and Keras2 with TensorFlow. First, they select a set of mainstream
 Slow Cellular Data Internet Speeds on iPhone: Fixes
May 03, 2024 pm 09:01 PM
Slow Cellular Data Internet Speeds on iPhone: Fixes
May 03, 2024 pm 09:01 PM
Facing lag, slow mobile data connection on iPhone? Typically, the strength of cellular internet on your phone depends on several factors such as region, cellular network type, roaming type, etc. There are some things you can do to get a faster, more reliable cellular Internet connection. Fix 1 – Force Restart iPhone Sometimes, force restarting your device just resets a lot of things, including the cellular connection. Step 1 – Just press the volume up key once and release. Next, press the Volume Down key and release it again. Step 2 – The next part of the process is to hold the button on the right side. Let the iPhone finish restarting. Enable cellular data and check network speed. Check again Fix 2 – Change data mode While 5G offers better network speeds, it works better when the signal is weaker
 The vitality of super intelligence awakens! But with the arrival of self-updating AI, mothers no longer have to worry about data bottlenecks
Apr 29, 2024 pm 06:55 PM
The vitality of super intelligence awakens! But with the arrival of self-updating AI, mothers no longer have to worry about data bottlenecks
Apr 29, 2024 pm 06:55 PM
I cry to death. The world is madly building big models. The data on the Internet is not enough. It is not enough at all. The training model looks like "The Hunger Games", and AI researchers around the world are worrying about how to feed these data voracious eaters. This problem is particularly prominent in multi-modal tasks. At a time when nothing could be done, a start-up team from the Department of Renmin University of China used its own new model to become the first in China to make "model-generated data feed itself" a reality. Moreover, it is a two-pronged approach on the understanding side and the generation side. Both sides can generate high-quality, multi-modal new data and provide data feedback to the model itself. What is a model? Awaker 1.0, a large multi-modal model that just appeared on the Zhongguancun Forum. Who is the team? Sophon engine. Founded by Gao Yizhao, a doctoral student at Renmin University’s Hillhouse School of Artificial Intelligence.
 Tesla robots work in factories, Musk: The degree of freedom of hands will reach 22 this year!
May 06, 2024 pm 04:13 PM
Tesla robots work in factories, Musk: The degree of freedom of hands will reach 22 this year!
May 06, 2024 pm 04:13 PM
The latest video of Tesla's robot Optimus is released, and it can already work in the factory. At normal speed, it sorts batteries (Tesla's 4680 batteries) like this: The official also released what it looks like at 20x speed - on a small "workstation", picking and picking and picking: This time it is released One of the highlights of the video is that Optimus completes this work in the factory, completely autonomously, without human intervention throughout the process. And from the perspective of Optimus, it can also pick up and place the crooked battery, focusing on automatic error correction: Regarding Optimus's hand, NVIDIA scientist Jim Fan gave a high evaluation: Optimus's hand is the world's five-fingered robot. One of the most dexterous. Its hands are not only tactile
 The first robot to autonomously complete human tasks appears, with five fingers that are flexible and fast, and large models support virtual space training
Mar 11, 2024 pm 12:10 PM
The first robot to autonomously complete human tasks appears, with five fingers that are flexible and fast, and large models support virtual space training
Mar 11, 2024 pm 12:10 PM
This week, FigureAI, a robotics company invested by OpenAI, Microsoft, Bezos, and Nvidia, announced that it has received nearly $700 million in financing and plans to develop a humanoid robot that can walk independently within the next year. And Tesla’s Optimus Prime has repeatedly received good news. No one doubts that this year will be the year when humanoid robots explode. SanctuaryAI, a Canadian-based robotics company, recently released a new humanoid robot, Phoenix. Officials claim that it can complete many tasks autonomously at the same speed as humans. Pheonix, the world's first robot that can autonomously complete tasks at human speeds, can gently grab, move and elegantly place each object to its left and right sides. It can autonomously identify objects



