 Technology peripherals
Technology peripherals
 AI
AI
 Basic computer problems, the maximum flow problem has made breakthrough progress: the new algorithm is 'ridiculously fast'
Basic computer problems, the maximum flow problem has made breakthrough progress: the new algorithm is 'ridiculously fast'
Basic computer problems, the maximum flow problem has made breakthrough progress: the new algorithm is 'ridiculously fast'

This problem is very basic in network flow theory. "The new algorithm is ridiculously fast. In fact, I was convinced that there was no such efficient algorithm for this problem," said Daniel Spielman from Yale University.
Maximum flows have been studied since the 1950s, when they were studied to model Soviet railway systems. "The study of it is even older than computer science theory," says Edith Cohen of Google's Mountain View, Calif., research center.
This question leads to many applications: Internet data streaming, airline scheduling, even matching job applicants to open positions. This new paper deals with both the maximum flow problem and the more general problem of handling maximum flow while also wishing to minimize cost. These two questions have inspired many significant advances in algorithmic technology over the years. "That's pretty much why we keep working in the field of algorithms," Spielman said. The new algorithm solves both problems in "approximately linear" time, which is to say that the algorithm's The running time is roughly proportional to the time required to record network details. No other algorithm for solving these problems can achieve this speed for all possible networks. Satish Rao of the University of California, Berkeley, said that this result made him jump: "It's simply amazing."
Spielman believes that we have found such a fast algorithm, and now it is It’s time to start thinking about solving various application problems that you haven’t thought of before.
Currently, the new method is mainly a theoretical improvement, because the improvement in algorithm speed is only applicable to much larger networks than those encountered in the real world. For these networks, the maximum Traffic problems can already be answered quickly (at least without considering cost minimization). Richard Peng of Canada's University of Waterloo, one of its six creators, expects the new algorithm could be in practical use within a year.
Some researchers believe that in the next few years, computer scientists may find ways to make it more practical, and maybe even faster.
Aleksander Mądry of MIT said that even with future improvements, the new paper is "the most exciting dunk in the slam dunk contest." He said it was basically the best."
One path at a time
Richard Peng said that so many computer scientists are working on the maximum flow problem that discussing past work at conferences is like passing the final credits of a movie. part. But most agree that the first formal algorithm was the 1956 application of a greedy algorithm for maximum flow by Lester Ford and Delbert Fulkerson, which uses the most readily available object at each step.You can think of this approach like this: First, imagine a highway network where you want to move as many delivery trucks as possible from Los Angeles to New York City in a given time period . Ford and Fulkerson's algorithm starts by choosing a path from Los Angeles to New York and routing as many trucks as possible along that path. This approach usually doesn't utilize the full capacity of all the roads on that particular road: if the road is a five-lane highway but it goes over a two-lane bridge, you can only have two trucks moving at any one time.
Next, the algorithm modifies the capacity of these segments to reflect that part of the segment's capacity is now used: it subtracts the number of trucks sent from the segment's capacity, so The five-lane highway now has a capacity of 3, while the two-lane bridge has a capacity of zero. At the same time, the algorithm adds 2 to the capacity of these roads in the reverse direction, so we can withdraw some of the traffic later if we wish.
The algorithm then finds a new path from Los Angeles to New York that can accommodate some trucks, sends as many trucks as possible along the path, and updates the capacity again. After a limited number of these steps, the road from Los Angeles to New York will no longer be able to accommodate any more trucks, and at this point the algorithm is complete: we simply combine all the traffic we built to get the maximum possible traffic of the network.
Ford and Fulkerson's algorithm does not attempt to make smart choices along the way. If it chooses a path that cuts off other useful paths, that's a problem for the algorithm to deal with later. In the decades since the algorithm was published, researchers have tried to speed up running times by having the algorithm make smarter choices, such as always using the shortest available path or the path with the greatest available capacity. In 1970, Yefim Dinitz discovered an efficient way to use all the shortest paths in a network in one step. The running time of this algorithm in low-capacity networks was proved by Shimon Even and Robert Tarjan to be m^1.5 (m: the number of links in the network. In contrast, the Ford-Fulkerson algorithm requires multiple m in low-capacity networks. ^2).
Nearly 30 years later, Rao and Andrew Goldberg came up with similar results for high-capacity networks. But no one can beat the m^1.5 index. "Going into the 21st century...the barriers to m^1.5 are deeply entrenched," said Sushant Sachdeva of the University of Toronto, one of the authors of the new paper. To make further progress, computer scientists must find ways to completely Different methods.
From Combinatorial to Calculus
So far all these algorithms have taken a combinatorial approach, looking for some type of structure at each step and Use this structure to update the stream. But in 2003, Spielman and ShangHua Teng of the University of Southern California opened the door to an entirely different approach to "optimization," in which calculus techniques are used as a guide to find optimal solutions.
Spielman and Teng developed a fast optimization algorithm that solves not the maximum flow problem, but a closely related problem of passing through each wire with a given resistance. The network finds the current with the lowest energy. Sachdeva said Spielman and Teng's progress were "critical moments."

Team members who created the ultra-fast algorithm to determine the maximum traffic and minimum cost of the network (clockwise from the upper left corner): Yang Liu, Li Chen, Rasmus Kyng, Maximilian Probst Gutenberg, Richard Peng, Sushant Sachdeva.
# Researchers soon began exploring how to apply this advance to the maximum flow problem. Think of the road network as a network of wires that add resistance on roads that don't have much available capacity, preventing electrons from traveling across them. Thanks to the work of Spielman and Teng, we can quickly calculate the current through these wires, and this model has rough properties for maximum vehicle flow through the highway. (They won't be exactly the same, since current issues don't put any hard limit on the capacity of the wire.)
Then, after generating this initial flow, we can do something like Ford and Fulkerson's combination The algorithm rescales the capacity the same. Next, the resistance of each wire can be reset to reflect these changing amounts and resolve the newly created circuit issues.
Unlike the combinatorial approach that changes one network block at a time, Spielman and Teng's optimization method completes the scan of the entire network each time. This makes each step more efficient, so fewer total steps are required to reach the maximum. In 2008, Samuel Daitch and Spielman of Google used this method, which basically matched the previous limit of maximum traffic of m^1.5. In 2013, Mądry advanced the approach further to exceed m^1.5 for low-capacity networks, improving runtimes to approximately a multiple of m^1.43. "It's shocking," Rao said.
Over the next few years, researchers expanded the method further, but their results remained stuck at m^1.33. They began to wonder whether this index was a fundamental limit.
For the maximum flow algorithm, the fastest imaginable running time should be m times (i.e. m^1.0), since writing down a network requires a multiple of m steps. This is called linear time. But to many researchers, such an extremely fast algorithm seemed unthinkable. "There's no good reason to believe we can do this," Spielman said.
Minify, reuse, recycle
The authors of this new paper believe that Daitch and Spielman’s approach has further advantages. Mądry had used it to reduce the number of steps required to solve the maximum flow problem, but this reduction came at a cost: at each step, the entire network had to be rewritten, and the power flow problem had to be solved from scratch.
This approach treats Spielman and Teng’s algorithm as a black box—no matter what is going on inside the algorithm. Six researchers decided to delve into the heart of the algorithm and tailor its components to the maximum flow problem. They suspect that these components might even allow them to solve the more difficult "minimum cost problem", in which it is to find the cheapest way to transport a given amount of material. Computer scientists have long known that any minimum cost algorithm can solve the maximum flow problem. Question.
As with other optimization methods, the researchers proposed the concept of flow "energy" as a function of link cost and capacity. Shifting traffic from expensive low-capacity links to cheap high-capacity links reduces the total energy of the system.
To figure out how to quickly move flows toward lower-energy states, the researchers combined this optimization approach with an old combinatorial perspective. The latter changes only one part of the network at a time, providing the possibility to reuse some of the work from previous steps.
At each step, the algorithm looks for a cycle that can reduce energy, that is, a path that starts and ends at the same point. The basic idea is simple: Suppose you create a toll road from Chicago to New York, and then you discover that there is a cheaper highway. At this point, adding New York to the loop, running along the expensive road to Chicago, and then back along the cheaper route, creates a loop that replaces the expensive path, thus reducing the overall cost of traffic.
This method uses many more steps than the "electrical method," so it sounds "like a step backwards" at first glance, says Valerie King of the University of Victoria in Canada. To compensate, the algorithm must find good loops at every step incredibly quickly, faster than it would take to examine the entire network.
This is how Spielman and Teng's algorithm works. Their algorithm provides a new way to use "low-stretch spanning trees", which are key to the algorithm and can capture many of the most salient features of a network. Given such a tree, it is always possible to construct at least one good cycle by adding a link outside the tree. Therefore, having a low-scaling spanning tree can greatly reduce the number of cycles that need to be considered.
Even so, in order to make the algorithm run quickly, the team could not build a new spanning tree at every step. Instead, they must ensure that each new cycle creates only a small ripple effect in the spanning tree so that most of the previous calculations are reused. Achieving this level of control is "the core difficulty," said Yang Liu, a graduate student at Stanford University and one of the paper's authors.
Ultimately, the researchers created an algorithm that runs in "almost linear" time, meaning that it runs closer to m as larger networks are used.
The algorithm borrows many ideas from Spielman and Teng and combines them into something entirely new. If you've only ever seen a horse-drawn cart, Spielman said, today's algorithms are like cars. "I see it has a place to sit, I see it has wheels, I see it has something to move it around. But they've replaced the horses with engines."
Rao speculated that the team's analysis was long and complex, but that other researchers would soon dig in to simplify the problem. "My feeling is that in the next few years, everything will get cleaner and better," he said. Once the algorithms are simplified, Spielman said, computer scientists may start to It is used as a subroutine of algorithms that solve different problems. "Now that we know we can do this very quickly, people will find all kinds of applications that they hadn't thought of before."
Additionally, the algorithm is The dizzying acceleration of the maximum flow problem made Spielman look forward to other core issues in algorithm theory, "What else can we do?"
The above is the detailed content of Basic computer problems, the maximum flow problem has made breakthrough progress: the new algorithm is 'ridiculously fast'. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1387
1387
 52
52
 Remote Desktop cannot authenticate the remote computer's identity
Feb 29, 2024 pm 12:30 PM
Remote Desktop cannot authenticate the remote computer's identity
Feb 29, 2024 pm 12:30 PM
Windows Remote Desktop Service allows users to access computers remotely, which is very convenient for people who need to work remotely. However, problems can be encountered when users cannot connect to the remote computer or when Remote Desktop cannot authenticate the computer's identity. This may be caused by network connection issues or certificate verification failure. In this case, the user may need to check the network connection, ensure that the remote computer is online, and try to reconnect. Also, ensuring that the remote computer's authentication options are configured correctly is key to resolving the issue. Such problems with Windows Remote Desktop Services can usually be resolved by carefully checking and adjusting settings. Remote Desktop cannot verify the identity of the remote computer due to a time or date difference. Please make sure your calculations
 2024 CSRankings National Computer Science Rankings Released! CMU dominates the list, MIT falls out of the top 5
Mar 25, 2024 pm 06:01 PM
2024 CSRankings National Computer Science Rankings Released! CMU dominates the list, MIT falls out of the top 5
Mar 25, 2024 pm 06:01 PM
The 2024CSRankings National Computer Science Major Rankings have just been released! This year, in the ranking of the best CS universities in the United States, Carnegie Mellon University (CMU) ranks among the best in the country and in the field of CS, while the University of Illinois at Urbana-Champaign (UIUC) has been ranked second for six consecutive years. Georgia Tech ranked third. Then, Stanford University, University of California at San Diego, University of Michigan, and University of Washington tied for fourth place in the world. It is worth noting that MIT's ranking fell and fell out of the top five. CSRankings is a global university ranking project in the field of computer science initiated by Professor Emery Berger of the School of Computer and Information Sciences at the University of Massachusetts Amherst. The ranking is based on objective
 Unable to open the Group Policy object on this computer
Feb 07, 2024 pm 02:00 PM
Unable to open the Group Policy object on this computer
Feb 07, 2024 pm 02:00 PM
Occasionally, the operating system may malfunction when using a computer. The problem I encountered today was that when accessing gpedit.msc, the system prompted that the Group Policy object could not be opened because the correct permissions may be lacking. The Group Policy object on this computer could not be opened. Solution: 1. When accessing gpedit.msc, the system prompts that the Group Policy object on this computer cannot be opened because of lack of permissions. Details: The system cannot locate the path specified. 2. After the user clicks the close button, the following error window pops up. 3. Check the log records immediately and combine the recorded information to find that the problem lies in the C:\Windows\System32\GroupPolicy\Machine\registry.pol file
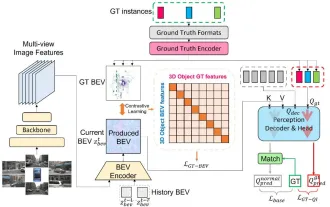 CLIP-BEVFormer: Explicitly supervise the BEVFormer structure to improve long-tail detection performance
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer: Explicitly supervise the BEVFormer structure to improve long-tail detection performance
Mar 26, 2024 pm 12:41 PM
Written above & the author’s personal understanding: At present, in the entire autonomous driving system, the perception module plays a vital role. The autonomous vehicle driving on the road can only obtain accurate perception results through the perception module. The downstream regulation and control module in the autonomous driving system makes timely and correct judgments and behavioral decisions. Currently, cars with autonomous driving functions are usually equipped with a variety of data information sensors including surround-view camera sensors, lidar sensors, and millimeter-wave radar sensors to collect information in different modalities to achieve accurate perception tasks. The BEV perception algorithm based on pure vision is favored by the industry because of its low hardware cost and easy deployment, and its output results can be easily applied to various downstream tasks.
 Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Common challenges faced by machine learning algorithms in C++ include memory management, multi-threading, performance optimization, and maintainability. Solutions include using smart pointers, modern threading libraries, SIMD instructions and third-party libraries, as well as following coding style guidelines and using automation tools. Practical cases show how to use the Eigen library to implement linear regression algorithms, effectively manage memory and use high-performance matrix operations.
 Explore the underlying principles and algorithm selection of the C++sort function
Apr 02, 2024 pm 05:36 PM
Explore the underlying principles and algorithm selection of the C++sort function
Apr 02, 2024 pm 05:36 PM
The bottom layer of the C++sort function uses merge sort, its complexity is O(nlogn), and provides different sorting algorithm choices, including quick sort, heap sort and stable sort.
 Can artificial intelligence predict crime? Explore CrimeGPT's capabilities
Mar 22, 2024 pm 10:10 PM
Can artificial intelligence predict crime? Explore CrimeGPT's capabilities
Mar 22, 2024 pm 10:10 PM
The convergence of artificial intelligence (AI) and law enforcement opens up new possibilities for crime prevention and detection. The predictive capabilities of artificial intelligence are widely used in systems such as CrimeGPT (Crime Prediction Technology) to predict criminal activities. This article explores the potential of artificial intelligence in crime prediction, its current applications, the challenges it faces, and the possible ethical implications of the technology. Artificial Intelligence and Crime Prediction: The Basics CrimeGPT uses machine learning algorithms to analyze large data sets, identifying patterns that can predict where and when crimes are likely to occur. These data sets include historical crime statistics, demographic information, economic indicators, weather patterns, and more. By identifying trends that human analysts might miss, artificial intelligence can empower law enforcement agencies
 Improved detection algorithm: for target detection in high-resolution optical remote sensing images
Jun 06, 2024 pm 12:33 PM
Improved detection algorithm: for target detection in high-resolution optical remote sensing images
Jun 06, 2024 pm 12:33 PM
01 Outlook Summary Currently, it is difficult to achieve an appropriate balance between detection efficiency and detection results. We have developed an enhanced YOLOv5 algorithm for target detection in high-resolution optical remote sensing images, using multi-layer feature pyramids, multi-detection head strategies and hybrid attention modules to improve the effect of the target detection network in optical remote sensing images. According to the SIMD data set, the mAP of the new algorithm is 2.2% better than YOLOv5 and 8.48% better than YOLOX, achieving a better balance between detection results and speed. 02 Background & Motivation With the rapid development of remote sensing technology, high-resolution optical remote sensing images have been used to describe many objects on the earth’s surface, including aircraft, cars, buildings, etc. Object detection in the interpretation of remote sensing images



