What did Tongji and Alibaba's CVPR 2022 Best Student Paper Awards study? This is an interpretation of one work

This article explains our work "EPro-PnP: Generalized End-to-End Probabilistic Perspective-n-Points for Monocular Object Pose Estimation" which won the CVPR 2022 Best Student Paper Award. The problem studied in this paper is to estimate the pose of an object in 3D space based on a single image. Among existing methods, pose estimation methods based on PnP geometric optimization often extract 2D-3D related points through deep networks. However, because the optimal solution of pose is not differentiable during backpropagation, it is difficult to use pose error as the The loss performs stable end-to-end training of the network, when the 2D-3D correlation points rely on the supervision of other agent losses, which is not an optimal training goal for pose estimation.

In order to solve this problem, we based on theory and proposed the EPro-PnP module, which outputs the probability density distribution of the pose instead of a single optimal solution of the pose, thus The non-differentiable optimal pose is replaced with a differentiable probability density, achieving stable end-to-end training. EPro-PnP is highly versatile and suitable for various specific tasks and data. It can be used to improve existing PnP-based pose estimation methods, or it can also use its flexibility to train new networks. In a more general sense, EPro-PnP essentially brings the common classification softmax into the continuous domain, and can theoretically be extended to train general models with nested optimization layers.

##Paper link: https://arxiv.org/abs/2203.13254

Code link: https://github.com/tjiiv-cprg/EPro-PnP

1. Preface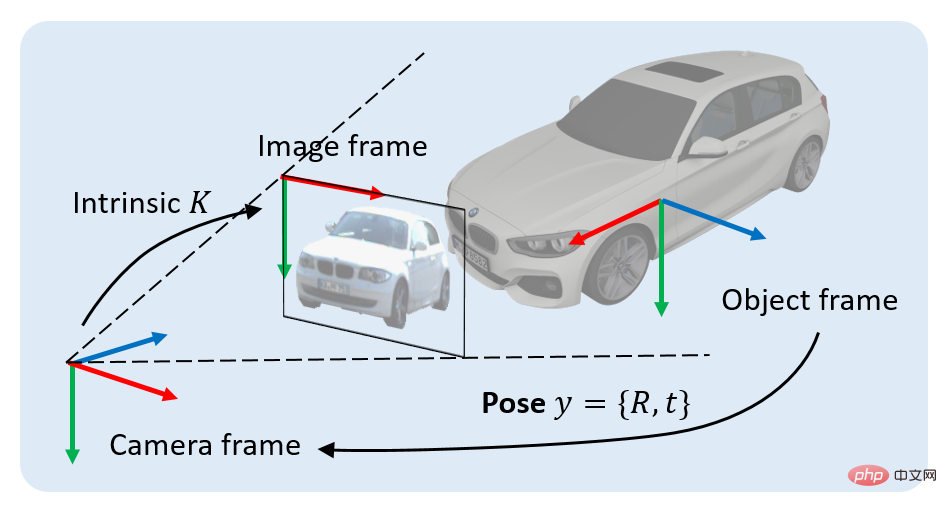

We study a classic problem in 3D vision: locating 3D objects based on a single RGB image. Specifically, given an image containing a projection of a 3D object, our goal is to determine the rigid body transformation from the object coordinate system to the camera coordinate system. This rigid body transformation is called the pose of the object, denoted as y, which contains two parts: 1) position component, which can be represented by a 3x1 displacement vector t, 2) orientation component, which can be represented by a 3x3 rotation matrix R means.

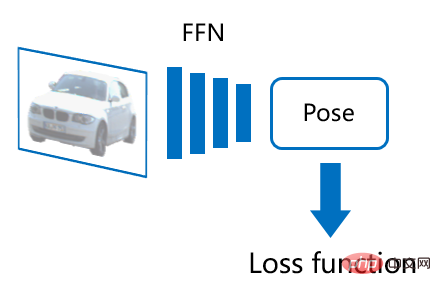
To address this problem, existing methods can be divided into two categories: explicit and implicit. The explicit method can also be called direct pose prediction, which uses a feedforward neural network (FFN) to directly output each component of the object's pose, usually: 1) Predict the object's pose Depth, 2) find out the 2D projection position of the object's center point on the image, 3) predict the object's orientation (the specific processing method of orientation may be more complicated). Using image data marked with the true pose of the object, a loss function can be designed to directly supervise the pose prediction results, easily achieving end-to-end training of the network. However, such networks lack interpretability and are prone to overfitting on smaller datasets. In 3D object detection tasks, explicit methods dominate, especially for larger datasets (such as nuScenes).

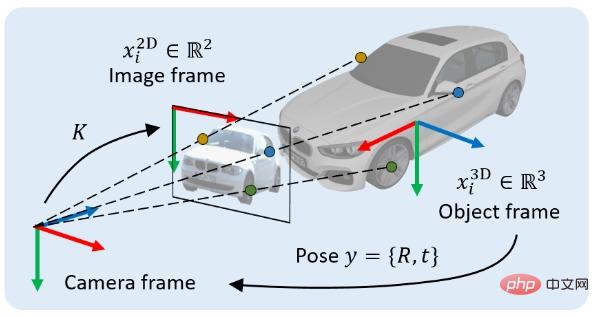
The implicit method is a pose estimation method based on geometric optimization. The most typical representative is the Pose estimation method based on PnP. In this type of method, you first need to find N 2D points in the image coordinate system (the 2D coordinates of the i-th point are marked ), and at the same time find the associated points in the object coordinate system. N 3D points (the 3D coordinates of the i-th point are marked as ), and sometimes it is necessary to obtain the associated weight of each pair of points (the associated weight of the i-th pair of points is marked as ). According to the perspective projection constraint, these N pairs of 2D-3D weighted associated points implicitly define the optimal pose of the object. Specifically, we can find the object pose that minimizes the reprojection error :

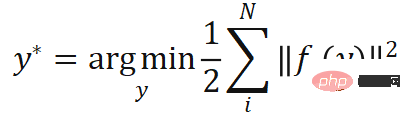
where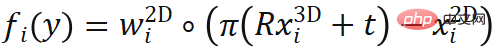, represents the weighted reprojection error, which is the function of pose. represents the camera projection function containing internal parameters, represents the element product. The PnP method is commonly used in 6-degree-of-freedom pose estimation tasks where the object geometry is known.

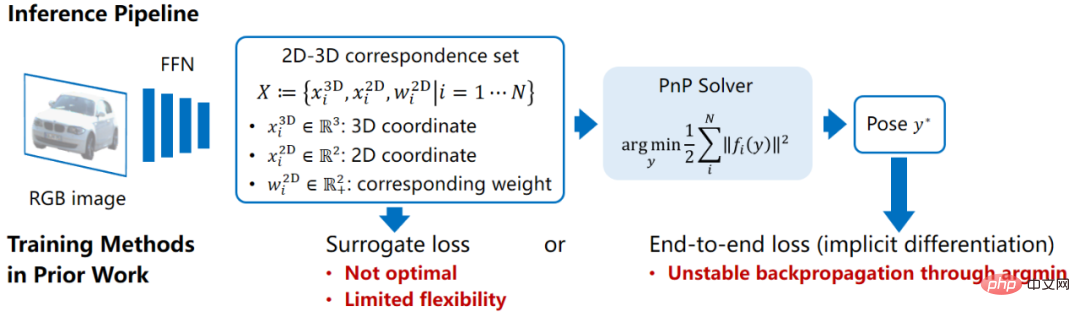
The PnP-based method also requires a feed-forward network to predict the 2D-3D associated point set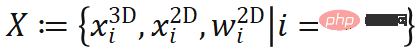. Compared with direct pose prediction, this deep learning model combined with traditional geometric vision algorithms has very good interpretability and its generalization performance is relatively stable. However, there are flaws in the model training methods in previous work. Many methods construct a proxy loss function to supervise the intermediate result X, which is not an optimal goal for pose. For example, if the shape of the object is known, the 3D key points of the object can be selected in advance, and then the network is trained to find the corresponding 2D projection point position. This also means that the surrogate loss can only learn some of the variables in X and is therefore not flexible enough. What if we don’t know the shapes of the objects in the training set and need to learn everything in X from scratch?

The explicit and implicit methods have complementary advantages. If the network can be trained end-to-end to learn the associated point set X by supervising the pose results output by PnP, the two can be combined Combining advantages. To achieve this goal, some recent studies have implemented backpropagation of PnP layers using implicit function derivation. However, the argmin function in PnP is discontinuous and non-differentiable at certain points, making backpropagation unstable and direct training difficult to converge.

2. Introduction to EPro-PnP method

1. EPro-PnP module

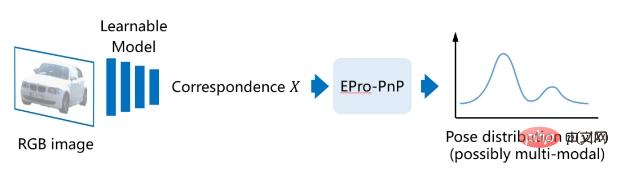
In order to achieve stable end-to-end For training, we propose end-to-end probabilistic PnP (end-to-end probabilistic PnP), namely EPro-PnP. The basic idea is to regard the implicit pose as a probability distribution, then its probability density is differentiable for X. First, define the likelihood function of the pose based on the reprojection error:

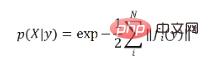
If an uninformative prior is used, then the posterior of the pose The probability density is the normalized result of the likelihood function:

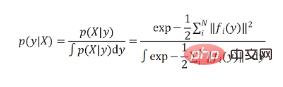
It can be noted that the above formula is consistent with the commonly used classification softmax formula points are close. In fact, the essence of EPro-PnP is to move the softmax from the discrete threshold to the continuous threshold, and replace the sum with an integral.

2. KL divergence loss

In the process of training the model, if the true pose of the object is known, it can be defined Target pose distribution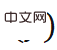. At this time, the KL divergence 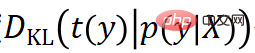can be calculated as the loss function used to train the network (because is fixed, it can also be understood as the cross-entropy loss function). When the target approaches the Dirac function, the loss function based on KL divergence can be simplified to the following form:

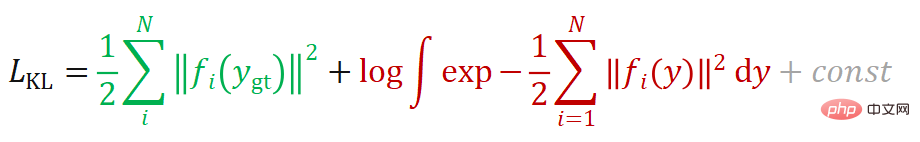
If you want to derive its derivative:

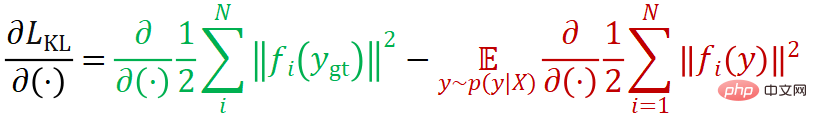
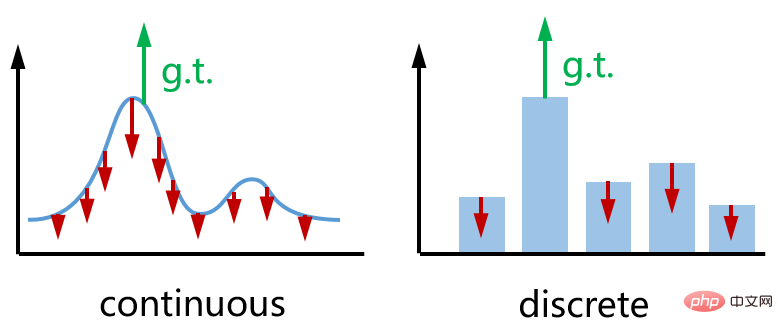
It can be seen that the loss function consists of two items. The first item (denoted as ) attempts to reduce the reprojection of the true value of the pose Error, the second term (denoted as ) attempts to increase the reprojection error everywhere in the predicted pose . The two directions are opposite, and the effect is shown in the figure below (left). As an analogy, the right side is the categorical cross-entropy loss that we commonly use when training classification networks.

3. Monte Carlo pose loss

It should be noted that the second term in KL loss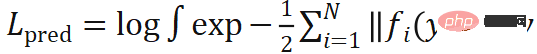 contains an integral. This integral has no analytical solution, so it must be approximated by numerical methods. Considering versatility, accuracy and computational efficiency, we use the Monte Carlo method to simulate the pose distribution through sampling.

Specifically, we used an importance sampling algorithm-Adaptive Multiple Importance Sampling (AMIS) to calculate K The pose sample 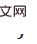with weight 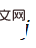, we call this process Monte Carlo PnP:

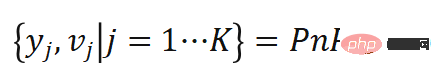
According to this, the second term can be approximated as a function about the weight 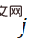, and 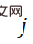can Back propagation:

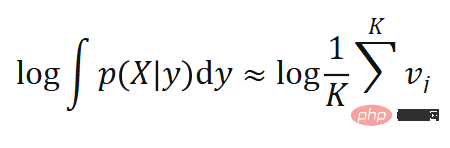
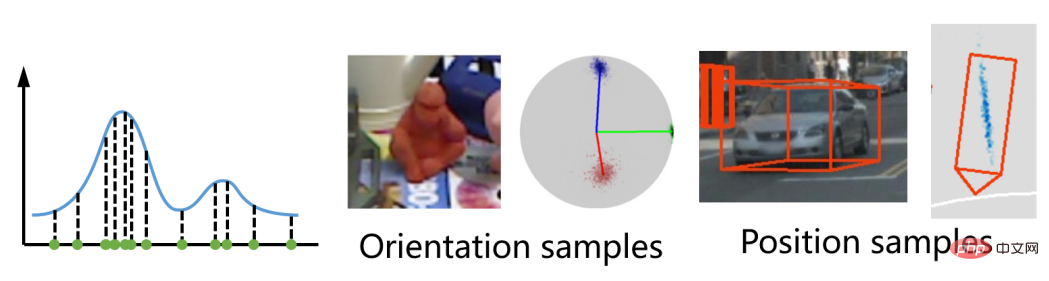
The visualization effect of pose sampling is as shown below:

4. Derivative regularization for PnP solver

Although Monte Carlo PnP loss can be used to train the network to obtain high-quality pose distribution, in the inference stage, PnP is still needed Optimize the solver to get the optimal pose solution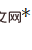. The commonly used Gauss-Newton algorithm and its derivatives solve 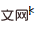through iterative optimization, and its iterative increment is determined by the first-order and second-order derivatives of the cost function . To make the solution of PnP 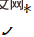closer to the true value 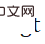, the derivative of the cost function can be regularized. The regularization loss function is designed as follows:

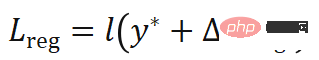
Among them, is the Gauss-Newton iteration increment, and the cost function The first-order and second-order derivatives are related and can be backpropagated. represents the distance metric, using smooth L1 for position and cosine similarity for orientation. When is inconsistent, this loss function causes the iteration increment to point to the actual true value.

3. Pose estimation network based on EPro-PnP

We use different subtasks for the 6-degree-of-freedom pose estimation and 3D target detection. network. Among them, for 6-degree-of-freedom pose estimation, it is slightly modified based on the CDPN network of ICCV 2019 and trained with EPro-PnP to conduct ablation studies; for 3D target detection, a brand-new network is designed based on the FCOS3D of ICCVW 2021. Deformable correspondence detection head to prove that EPro-PnP can train the network to directly learn all 2D-3D points and association weights without object shape knowledge, thus demonstrating the flexibility of EPro-PnP in applications.

1. Dense correlation network for 6-DOF pose estimation

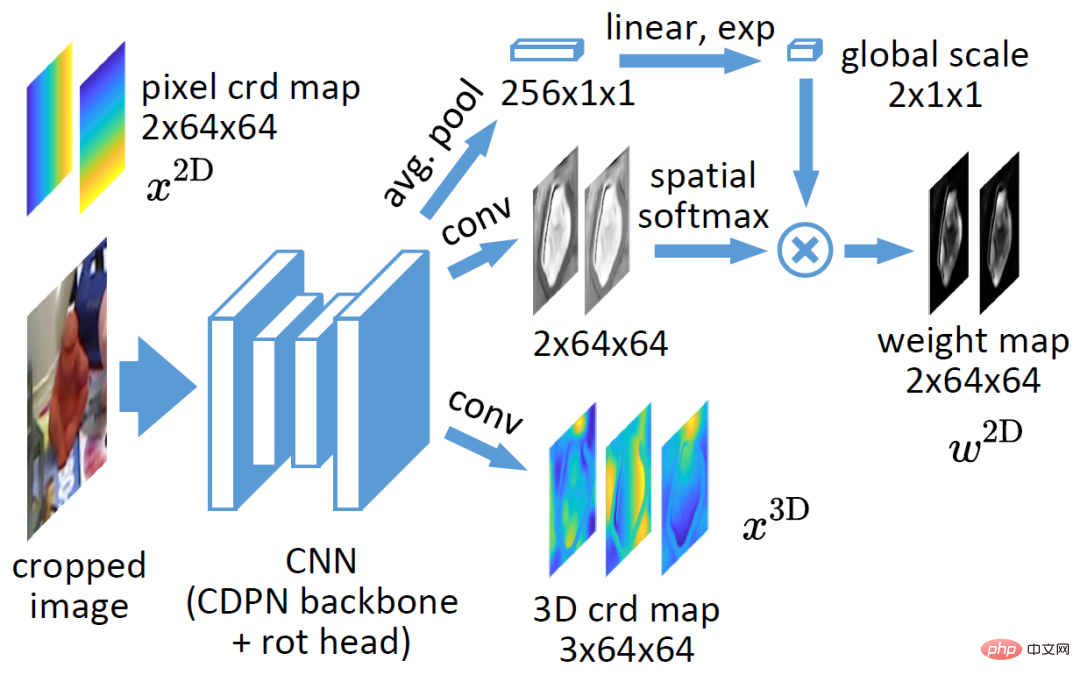
The network structure is shown in the figure above, except that the output layer is modified based on the original CDPN. The original CDPN uses the detected object 2D box to crop out the regional image and inputs it into the ResNet34 backbone. The original CDPN decouples position and orientation into two branches. The position branch uses the explicit method of direct prediction, while the orientation branch uses the implicit method of dense association and PnP. In order to study EPro-PnP, the modified network only retains the dense correlation branch, whose output is a 3-channel 3D coordinate map, and a 2-channel correlation weight, where the correlation weight has undergone spatial softmax and global weight scaling. The purpose of adding spatial softmax is to normalize the weight so that it has properties similar to attention map and can focus on relatively important areas. Experiments have proved that weight normalization is also the key to stable convergence. Global weight scaling reflects the concentration of pose distribution. The network can be trained with only the Monte Carlo pose loss of EPro-PnP, in addition to adding derivative regularization and an additional 3D coordinate regression loss when the object shape is known.

2. Deformation correlation network for 3D target detection

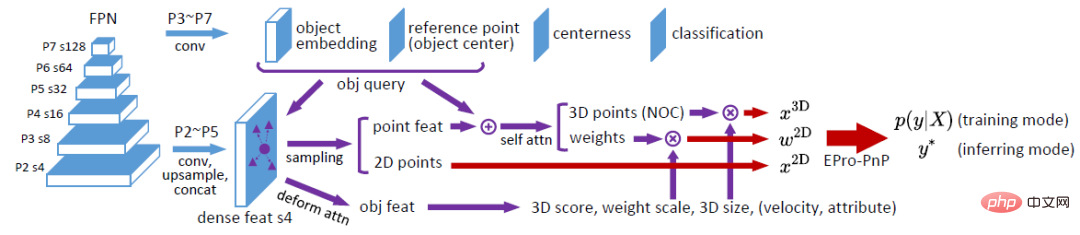
The network structure is shown in the figure above. Generally speaking, it is based on the FCOS3D detector and refers to the network structure designed by deformable DETR. Based on FCOS3D, its centerness and classification layers are retained, and its original pose prediction layer is replaced by object embedding and reference point layers for generating object query. Referring to deformable DETR, we get the 2D sampling position by predicting the offset relative to the reference point (so we get ). The sampled features are aggregated into object features through attention operations, which are used to predict object-level results (3D score, weight scale, 3D box size, etc.). In addition, after sampling, the features of each point are added with object embedding and processed by self attention to output the 3D coordinates and associated weights 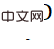corresponding to each point. All the predicted can be obtained by the Monte Carlo pose loss training of EPro-PnP, which can converge and achieve high accuracy without additional regularization. On this basis, derivative regularization loss and auxiliary loss can be added to further improve accuracy.

4. Experimental results

1. 6-degree-of-freedom pose estimation task

Using LineMOD data set Experiments and strict comparison with CDPN baseline, the main results are as above. It can be seen that by adding EPro-PnP loss for end-to-end training, the accuracy is significantly improved (12.70). Continue to increase the derivative regularization loss, and the accuracy is further improved. On this basis, using the training results of the original CDPN to initialize and increase epochs (keeping the total number of epochs consistent with the complete three-stage training of the original CDPN) can further improve the accuracy. Part of the advantage of pre-training CDPN comes from the additional training of CDPN. mask supervision.

The above figure is a comparison of EPro-PnP with various leading methods. EPro-PnP, which is improved from the backward CDPN, is close to SOTA in accuracy, and the architecture of EPro-PnP is simple. It is completely based on PnP for pose estimation and does not require additional explicit depth estimation or pose refinement. Therefore, in There are also advantages in efficiency.

2. 3D target detection task

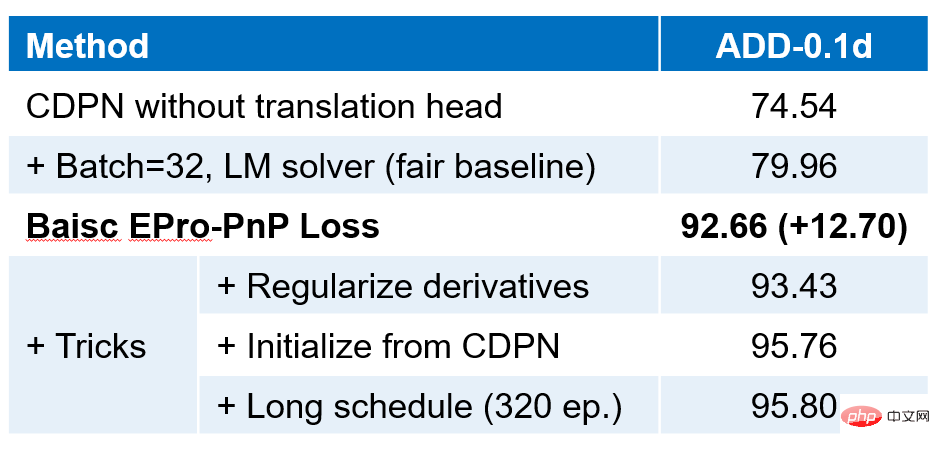
Using the nuScenes data set experiment, the results compared with other methods are shown in the figure above. EPro-PnP not only has a significant improvement over FCOS3D, but also surpasses PGD, another improved version of SOTA and FCOS3D at the time. More importantly, EPro-PnP is currently the only one that uses geometric optimization methods to estimate pose on the nuScenes dataset. Due to the large scale of the nuScenes data set, the end-to-end trained direct pose estimation network already has good performance, and our results illustrate that end-to-end training of a model based on geometric optimization can achieve better performance on large data sets. Excellent performance.

3. Visual analysis

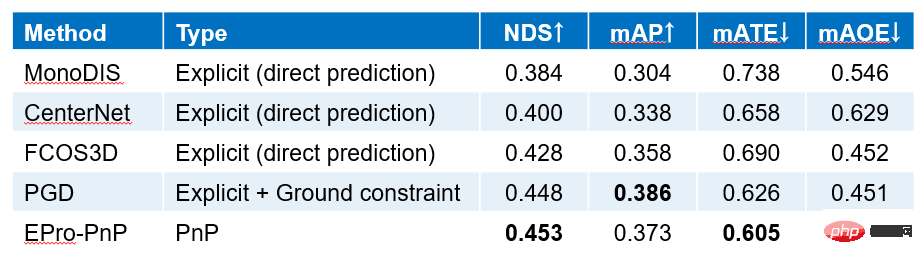
The above figure shows the prediction results of the dense association network trained with EPro-PnP. Among them, the correlation weightgraph highlights important areas in the image, similar to the attention mechanism. From the loss function analysis, it can be seen that the highlight area corresponds to the area with low reprojection uncertainty and which is more sensitive to pose changes.

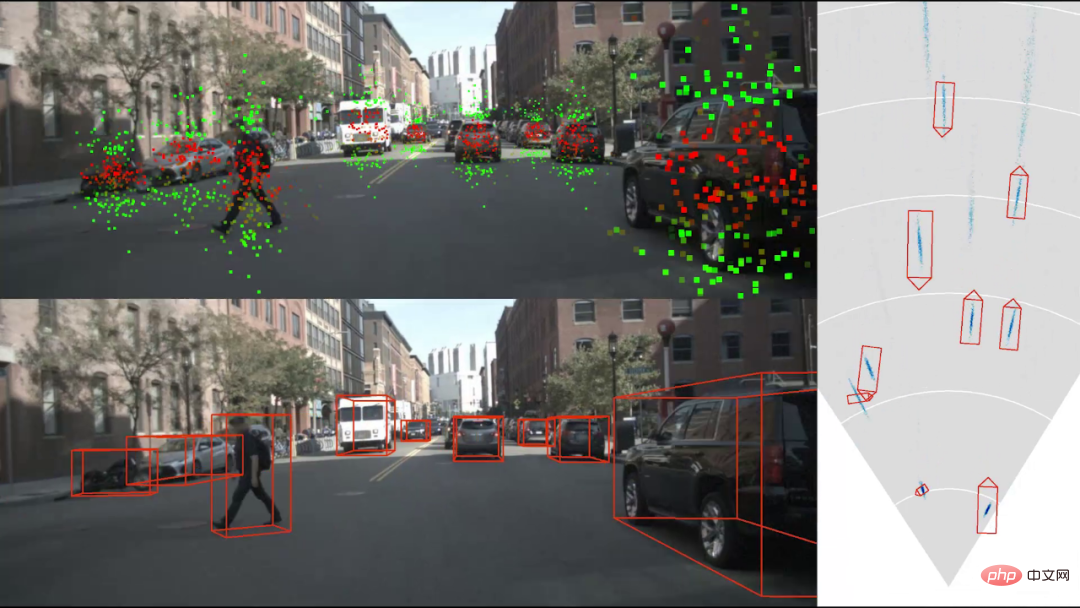
#The results of 3D target detection are shown in the figure above. The upper left view shows the 2D point positions sampled by the deformation correlation network. Red indicates that the horizontal X component is higher, and green indicates that the vertical Y component is higher. High point. The green dots are generally located at the upper and lower ends of the object. Their main function is to calculate the distance of the object through the height of the object. This feature is not artificially specified and is completely the result of free training. The picture on the right shows the detection results in a top view, in which the blue cloud image represents the distribution density of the center point of the object, reflecting the uncertainty of the object's positioning. Generally, the positioning uncertainty of distant objects is greater than that of nearby objects. 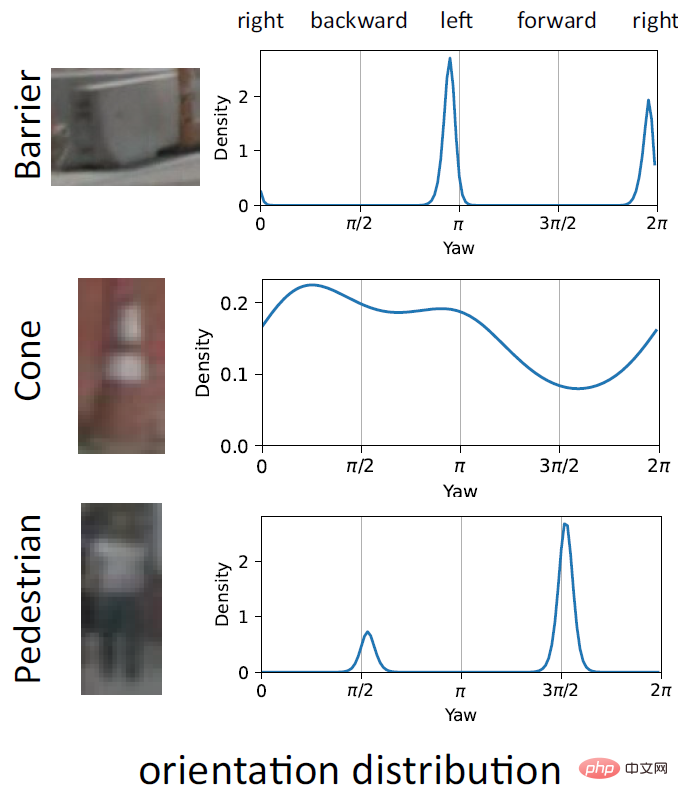Another important advantage of EPro-PnP is the ability to represent orientation ambiguity by predicting complex multimodal distributions. As shown in the figure above, Barrier often has two peaks with a difference of 180° due to the rotational symmetry of the object itself; Cone itself has no specific orientation, so the prediction results are distributed in all directions; Pedestrian is not completely rotationally symmetrical, but due to the image It's not clear, it's hard to tell the front and back, and sometimes there are two peaks. This probabilistic characteristic makes EPro-PnP do not require any special processing on the loss function for symmetric objects.

5. Summary

EPro-PnP transforms the originally undifferentiable optimal pose into a differentiable pose probability density, making the position based on PnP geometric optimization The pose estimation network enables stable and flexible end-to-end training. EPro-PnP can be applied to general 3D object pose estimation problems. Even when the 3D object geometry is unknown, the 2D-3D associated points of the object can be learned through end-to-end training. Therefore, EPro-PnP broadens the possibilities of network design, such as our proposed deformation correlation network, which was previously impossible to train.

In addition, EPro-PnP can also be directly used to improve existing PnP-based pose estimation methods, releasing the potential of existing networks through end-to-end training and improving pose estimation accuracy. In a more general sense, EPro-PnP essentially brings the common classification softmax into the continuous domain. It can not only be used for other 3D vision problems based on geometric optimization, but can also be theoretically extended to train general nested optimization layers. model.

The above is the detailed content of What did Tongji and Alibaba's CVPR 2022 Best Student Paper Awards study? This is an interpretation of one work. For more information, please follow other related articles on the PHP Chinese website!