Human beings need to master a lot of knowledge points to solve a large number of mathematical problems at different stages of their growth process. However, understanding the knowledge points does not mean you really understand it. Only by being able to solve the problems can you reflect human wisdom. In recent years, neural networks have achieved great success in fields such as computer vision, pattern matching, natural language processing, and reinforcement learning. However, the discrete combinatorial reasoning ability of neural network models is far less than that of humans. So, can neural networks understand mathematical problems and solve them? If so, how good is the problem-solving ability of neural networks?
In terms of data form, a mathematical problem can be regarded as a sequence, and its solution (problem-solving steps or expressions) is often presented in the form of a sequence. Then solving mathematical problems can be regarded as a translation problem from natural language to mathematical language. The neural network model can formally solve mathematical problems. It can be known from various previous research works that neural networks can achieve very good performance on translation problems and have surpassed human performance on multiple data sets. However, it is significantly different from machine translation. In addition to the ability to understand the semantics of the question, solving mathematical problems often requires the model to have the ability to reason about discrete combinations of algebraic generalized objects and entities.
In order to explore the deep model’s ability to solve mathematical problems, the Sun Yat-sen University Human-Machine Intelligence Integration Laboratory used primary and secondary school mathematics application problems and geometric calculation problems based on previous research. To get started, a series of studies were carried out to improve the semantic understanding, cognitive reasoning and mathematical problem-solving capabilities of deep models. This article will briefly introduce a series of research in the field of mathematical problem solving by the Human-Machine-Object Intelligent Integration Laboratory of Sun Yat-sen University.
Paper 1: Semantically-Aligned Universal Tree-Structured Solver for Math Word Problems
The 2020 Conference on Empirical Methods in Natural Language Processing
##Paper address: https://aclanthology. org/2020.emnlp-main.309.pdf
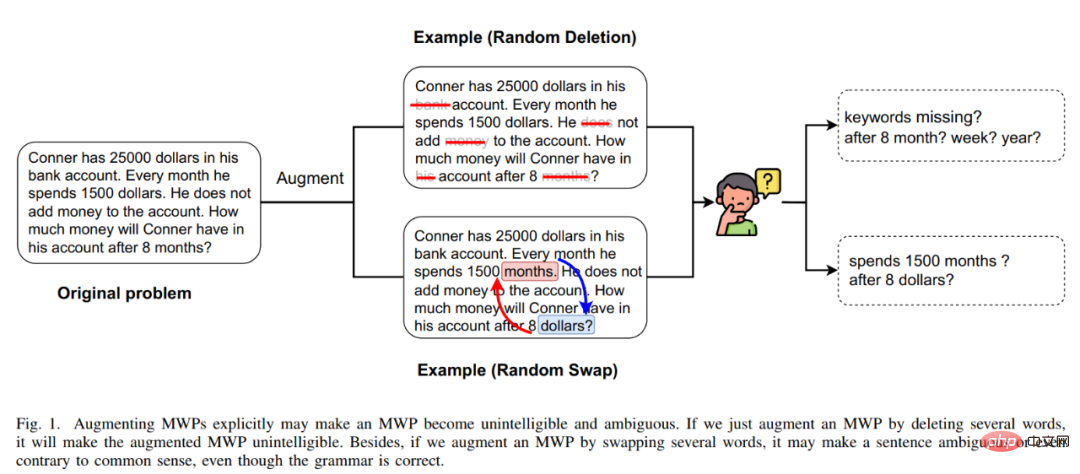
#A practical math word problem solver should be able to solve various types of math word problems, such as linear equations of one variable, Systems of linear equations of two variables, quadratic equations of one variable, etc. However, most mathematical application problem solving work is only designed for four arithmetic operations, and this type of design is often difficult to expand to more question types. It is impossible to use a unified mathematical application problem solver to solve various types of expressions at the same time. Application questions. In addition, most current mathematical word problem solvers lack semantic constraints between the problem text and the solution expression.
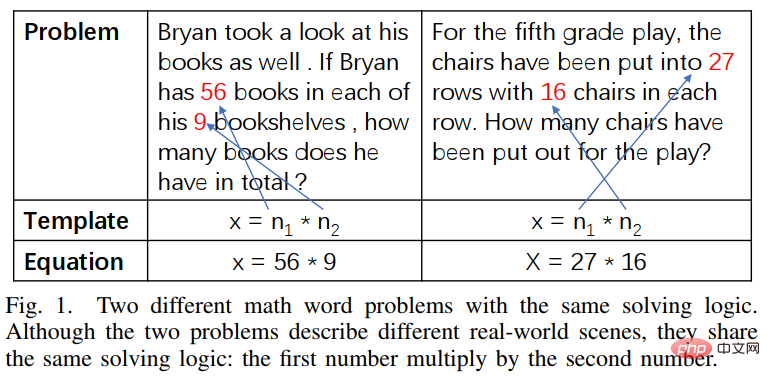
In response to the above problems, the Sun Yat-sen University Human-Machine Intelligence Integration Laboratory team proposed a unified expression tree representation scheme. By introducing additional operators to connect multiple expressions, one-yuan Expressions of linear equations, linear equations of two variables, quadratic equations of one variable and other types of expressions can be expressed in a unified manner, which can simplify the design of the solver and solve various types of application problems, as shown in Figure 1.
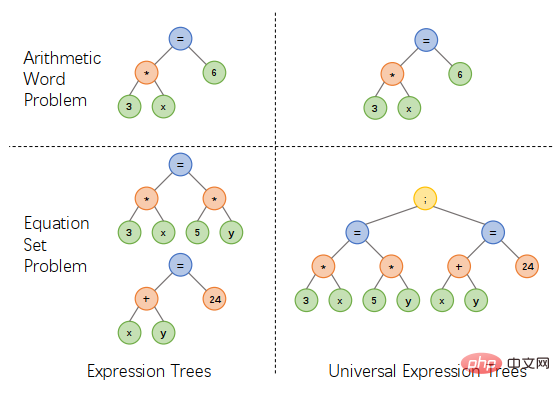
Figure 1 Unified expression tree representation scheme design
Based on the unified expression tree representation scheme, we further propose a semantically aligned tree structure universal solver (SAU-Solver), as shown in Figure 2. Our tree-structured universal solver consists of two parts, a problem encoder based on a two-layer GRU and a tree-structured decoder based on a unified expression tree representation. And during the training process, we introduced semantic alignment regularization. By constraining the consistency of the expression subtree and the question context, our general solver can more fully consider the semantic relationship between the problem and the expression, and explore various types of problems. Mathematical knowledge, thus improving the expression generation capabilities of the solver.
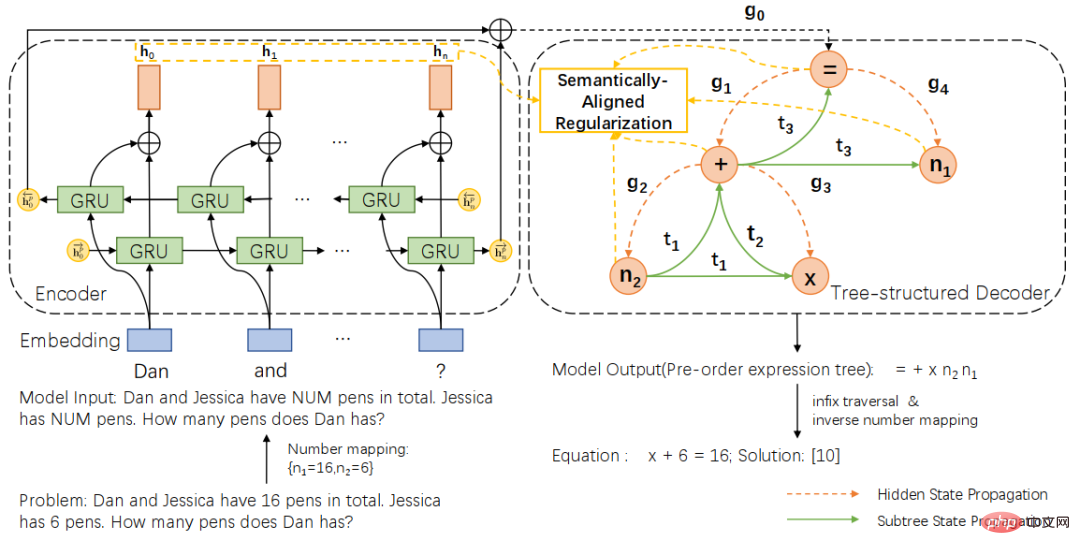
Figure 2 Semantic alignment tree structure solver
In addition, in order to better measure the versatility and solving capabilities of the solver, we also constructed a medium-sized multi-question data set HMWP for problems with a single type of questions in the current annotation data set. The data set includes thousands of mathematical text questions that solve various expression types such as linear equations of one variable, systems of linear equations of two variables, quadratic equations of one variable, etc. Our experiments show that data sets with multiple question types are more challenging for solvers than data sets with a single type. They can also better measure the solver's problem-solving ability and promote research in the solver community.
In the experiment, the article compared the proposed SAU-Solver with existing methods in HMWP, Math23K, ALG514 and Dolphin18K-Manual. The experimental results are shown in the figure below, which proves the versatility and better mathematical problem-solving ability of our method.
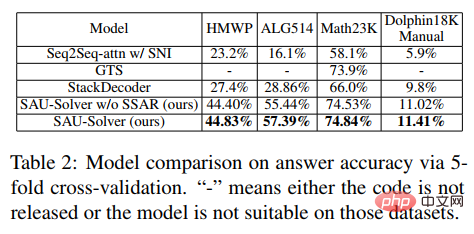
For more research details, please refer to the original paper.
Paper 2: Neural-Symbolic Solver for Math Word Problems with Auxiliary Tasks
The 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing
Paper address: https://arxiv.org/abs/2107.01431
The current solver for elementary mathematics application problems does not consider various mathematical symbol constraints, but only simple Problems solved using an encoder-decoder framework improperly, leading to unreasonable predictions. The introduction of symbolic constraints and symbolic reasoning is very critical for automatically solving mathematical application problems.
Therefore, the Sun Yat-sen University Human-Machine Intelligence Integration Laboratory team introduced the neuro-symbolic computing paradigm and proposed a new neuro-symbolic solver (NS-Solver) to assist in the task Perform explicit knowledge injection to achieve different levels of symbolic constraints. Its technical architecture is shown in Figure 3. NS-Solver is built on the backbone of the network by three components: 1) Problem Reader, which performs efficient semantic understanding and representation of mathematical problems through a two-layer bidirectional GRU network; 2) Programmer, which is responsible for symbolic reasoning based on problem semantics and common sense prediction results. , generate the solution expression. 3) Executor, use the sympy library to solve expressions and obtain the final answer.
Regarding symbol constraints, we propose a variety of auxiliary tasks to use additional training signals and common sense prediction results to explicitly constrain the symbol table and reduce the problem solving search space: 1) Self-supervised number prediction task: better understand the semantics of the question by predicting the position and number of numbers in the question; 2) Common sense quantifier prediction task: inject common sense knowledge and use the prediction results to constrain the symbol table and reduce the search space; 3) Consistency Check: Check the consistency between the output of the solver and the target expression from the semantic level; 4) Dual utilization task: Strengthen the problem semantic understanding of the solver through the two-way constraints from problem to expression and expression to problem.
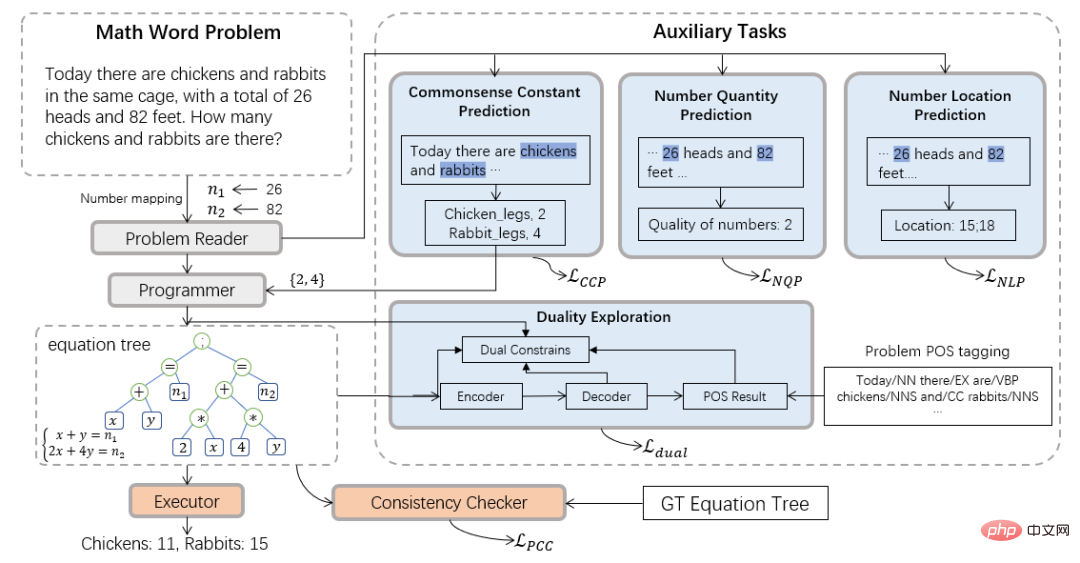
##Figure 3 Neural-Symbolic Solver (NS-Solver)
In addition, in order to better verify the performance of the solver, we also constructed a larger multi-question mathematical application problem data set CM17K to better promote research in the mathematical problem solving community. CM17K contains 6215 four-variable arithmetic problems, 5193 linear equations of one variable, 3129 nonlinear equations of one variable and 2498 equations. The statistics of CM17K and Math23K are shown in the table below. It can be seen from the statistics that CM17K has longer question information, longer solution expressions, and involves more common sense than Math23K, which means that CM17K better characterizes the performance of the problem solver in terms of solving difficulty. .
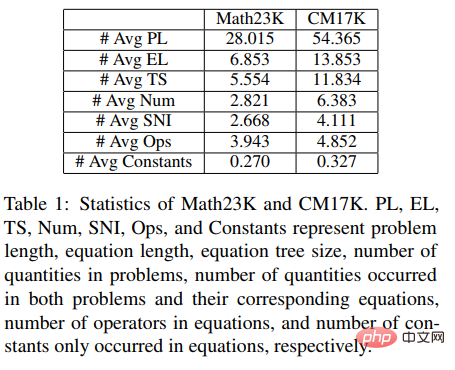
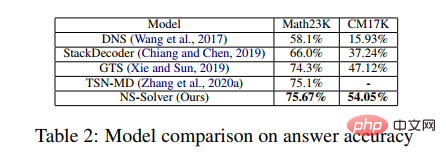
In the experiment, the article compared the proposed NS-Solver with existing methods on Math23K and CM17K, and conducted ablation experiments to prove that NS-Solver Good problem-solving skills and versatility. The experimental results are shown in the following two tables.
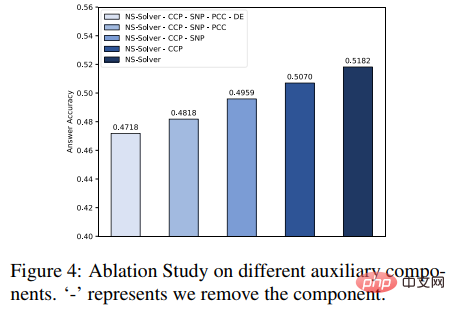
In addition, we also conducted ablation experiments on auxiliary tasks, as shown in the figure below. The experimental results prove that each auxiliary task can improve the problem-solving ability of NS-Solver.
For more research details, please refer to the original paper.
Paper 3: GeoQA – A Geometric Question Answering Benchmark Towards Multimodal Numerical Reasoning
Findings of the Association for Computational Linguistics: ACL-IJCNLP 2021
Paper address: https://arxiv .org/pdf/2105.14517.pdf
Automatic mathematical problem solving has gained more and more attention recently. Automatic Mathematical Problem Solving Most work focuses on automatically solving mathematical word problems. However, few works focus on geometry problems. Compared with mathematics application questions, geometry questions require the understanding of text descriptions and graphics and charts at the same time, because in geometry questions, the question text and graphics and charts usually complement each other and are indispensable. Existing methods for automatically solving geometry problems are highly rule-dependent and only evaluated on small data sets.
Figure 4 Sample geometry question
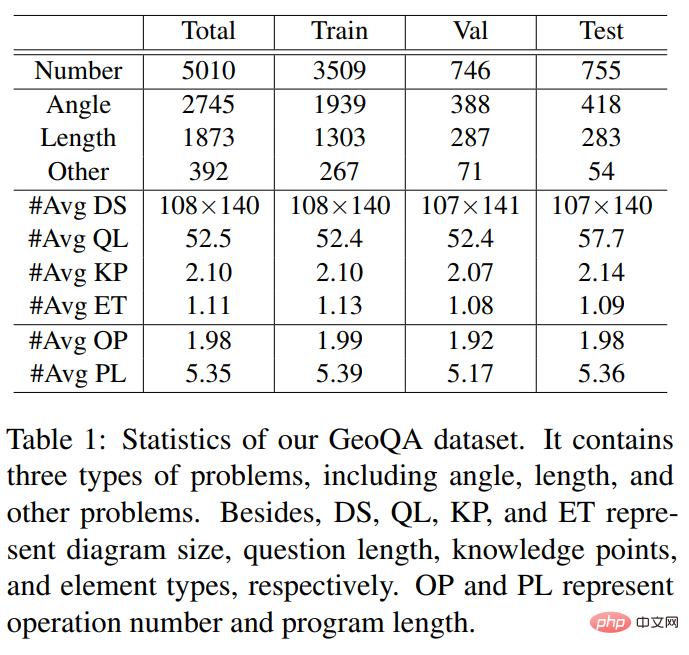
In order to promote research on automatic solution of geometric problems, the Sun Yat-sen University Human-Machine Intelligence Integration Laboratory team constructed a question and answer data set GeoQA consisting of 5010 geometric multiple-choice questions. As shown in Figure 4, each sample in the GeoQA data set has a question description, geometric image, question options, answers, question type, knowledge points, solution analysis, and formal procedures marked by problem-solving steps. In terms of problem size, this dataset is 25 times larger than the GeoS dataset commonly used in previous work. The relevant statistical information of the GeoQA dataset is shown in the table below.
The formal program operators and the constants involved used by the GeoQA data set are shown in the following table.
In order to better promote the research of geometric problem solvers, in addition to building some baseline models based on the GeoQA data set, we also The neurogeometric problem solver NGS is proposed to understand multi-modal semantic information and generate interpretable formal programs. The overall design of the neurogeometric problem solver NGS is shown in Figure 5.
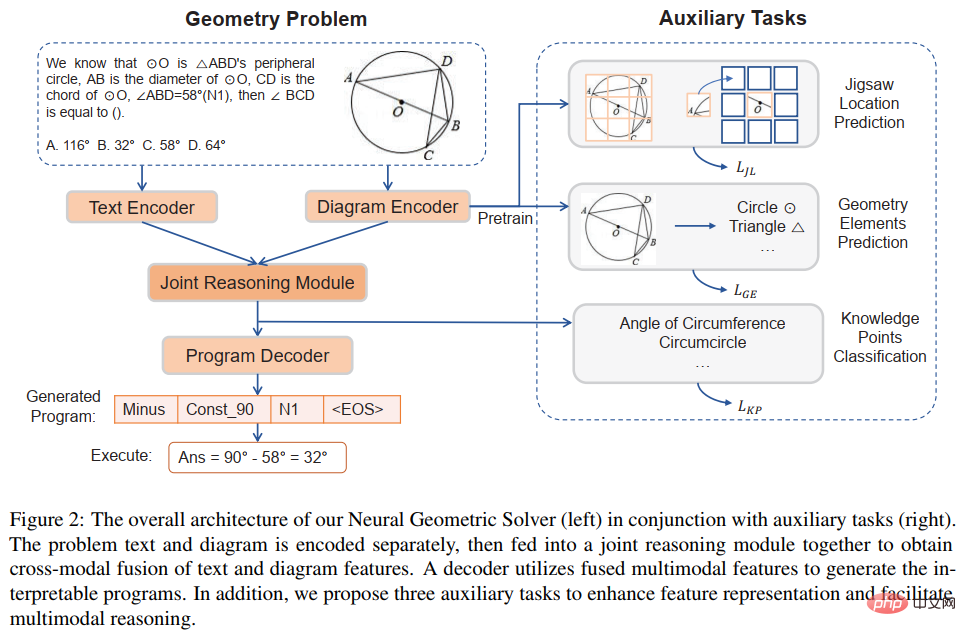
##Figure 5 Schematic diagram of the Neurogeometry Problem Solver (NGS)
Our NGS mainly consists of text encoder, geometry encoder, joint reasoning module and program decoder. The text encoder is responsible for the semantic representation of the question text, and the geometric figure encoder is responsible for the representation of geometric figures. Both text representation and graphical representation will be input to the joint reasoning model for multi-modal semantic representation, and fed to the program decoder for program decoding, and an interpretable and executable formal solution program will be output.
In addition, in order to enhance the representation ability of geometric figures by the geometric figure encoder and promote the joint reasoning module to fully integrate and efficiently express the multi-modal information contained in the question, we also introduce A variety of auxiliary tasks are implemented to improve the representation ability of the model and inject theorem knowledge. These auxiliary tasks include: 1) Puzzle position prediction: pixel-level graphics understanding of geometric figures is achieved by cutting the geometric figures into multiple patches, randomly arranging them, and then letting the geometry encoder rearrange them; 2) Geometric elements Prediction: Let the geometric figure encoder learn to predict which geometric elements appear in the current geometric figure to achieve object-level graphics understanding; 3) Knowledge point prediction: perform multi-modal fusion of question text representation and geometric figure representation in the joint reasoning module At the same time, the knowledge point classification task is introduced to improve the overall problem representation. In NGS, we pre-train the geometry encoder using puzzle position prediction and geometry element prediction. The knowledge point prediction task is used as a subtask for multi-task training with NGS.
In the experiment, the article built multiple neural network-based baseline models based on GeoQA and compared NGS with them. The experimental results of NGS and baseline models on GeoQA are shown in the table below.
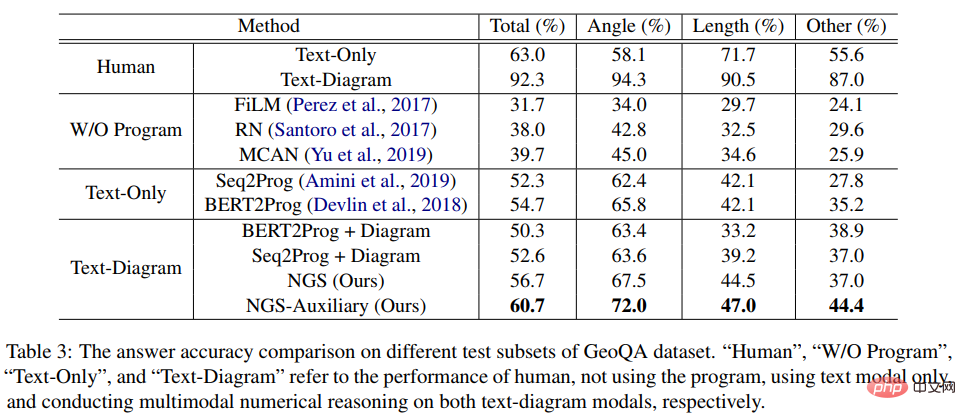
As can be seen from the above table, NGS can achieve better problem-solving performance on GeoQA than the baseline model. However, we can also see that there is still a large gap between various models and humans in solving geometric problems.
In addition, we conducted various ablation experiments to verify the effectiveness of various designs in NGS. For more research details, please refer to the original paper.
Paper 4: Unbiased Math Word Problems Benchmark for Mitigating Solving Bias
Findings of the Association for Computational Linguistics: NAACL 2022
##Paper address: https://aclanthology.org/2022 .findings-naacl.104.pdf
In this work, the Sun Yat-sen University Human-Machine Intelligence Integration Laboratory team re-examines the evaluation on the current benchmark for solving mathematical application problems The solving bias of the model. This problem-solving bias is mainly caused by data bias and learning bias. Data bias refers to the problem that the training data set fails to cover all the different narrative methods of each question. As a result, the problem-solving model can only learn shallow semantics and fails to understand the deep semantics of the question meaning, such as As shown in Figure 6(a), since the problem-solving model only learns shallow semantics and uses it to solve problems, even after we remove the problem part of the problem, the problem solver can still reach 69.4%.
The learning bias means that a MWP can be solved by multiple equivalent expressions, but the current data sets only use one of the equivalent equations as a label. Forcing the model to learn this label while ignoring other equivalent equations leads to a bias in learning training. As shown in Figure 6(b), during the training process, the model may generate an expression that is inconsistent with the GroundTruth expression but the answer is correct. However, because the data set only uses a certain equivalent expression as a label, it will lead to When calculating the loss function, the expression is considered to be an incorrect expression, and the loss between the two correct expressions is back-propagated to the solution model, resulting in overcorrection of the model.
Figure 6 Example of data bias and learning bias
In order to alleviate data bias, the Sun Yat-sen University Human-Machine Intelligence Integration Laboratory team made a new attempt. We re-labeled a new MWP in a way that covers the question questions as much as possible. Benchmark UnbiasedMWP. We collected 2907 word problems as basic questions, and then we annotated as many questions as possible for the stories contained in each question.
In order to simplify the manual annotation process, we first generate some reasonable expressions based on the backbone content of the question, and then rewrite the question in reverse. In order to generate reasonable expressions, we designed three expression variants: 1) Variable assortment (Va) variant: randomly select two numeric variables from the backbone of the question, and use mathematical operators (, -, *, /) to They combine, for example n0 n1, n0 − n1 etc. 2) Subexpression (Sub) transformation: All subexpressions contained in the target expression of the original question are modified by operators, thereby obtaining a new expression. 3) Whole-expression (Whole) deformation: obtain a new expression by changing the operators contained in the target expression of the original question. The new expression sets obtained from the above three variants are manually filtered, expressions that cannot be annotated with new questions are filtered out, and the remaining expressions are manually annotated with questions.
In order to alleviate the learning bias, we propose a dynamic target selection strategy. During the training process, based on the results of the model output, a target expression closer to it is selected as the GroundTruth . In order to obtain equivalent expressions, we use the commutative law in mathematical operations to deform the expression tree to obtain multiple equivalent expressions. As shown in Figure 7.
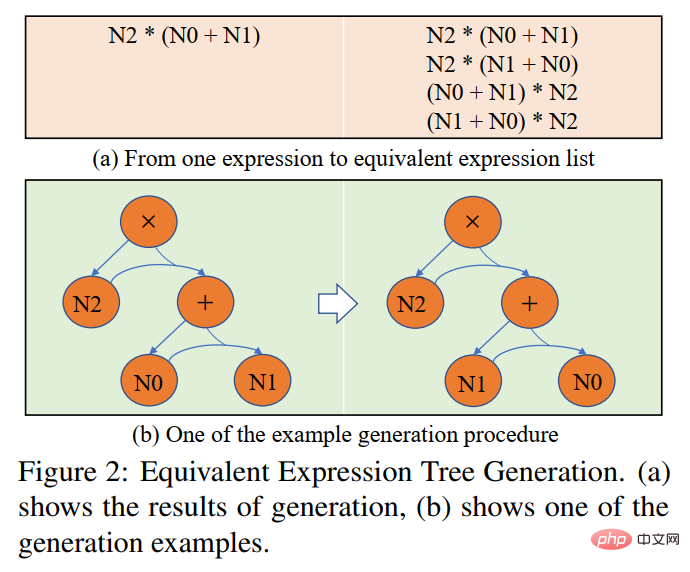
Figure 7 Schematic diagram of equivalent expression tree generation
In the experiment, the article first verified the UnbiasedMWP data set on multiple SOTA baseline models. The experimental results are shown in the table below.
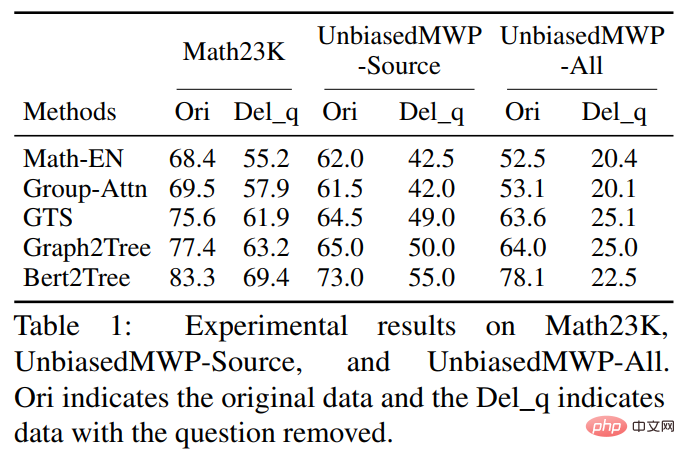
It can be seen from the experimental results that compared to the existing Math23K, our data set UnbiasedMWP has less data bias because When we removed the question, the model's solving performance dropped sharply, which proved from the side that our data set made the model need to pay attention to deep semantic information to solve the problem.
In order to verify whether our dynamic target selection strategy can reduce learning bias, we applied the dynamic target selection strategy to multiple problem-solving models. The experimental results are shown in the table below.
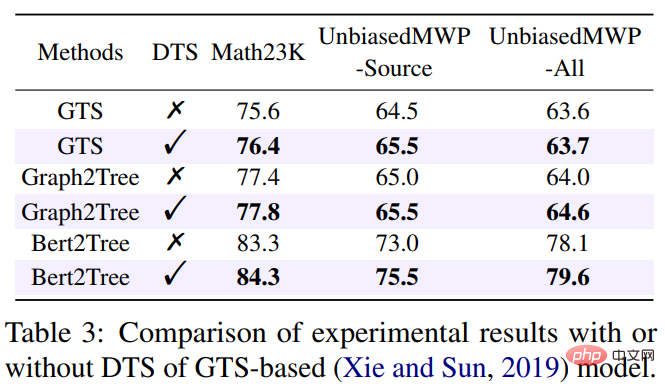
It can be seen from the experimental results that our dynamic target selection strategy can effectively reduce the learning bias and improve the solution effect of the model. For more research details, please refer to the original paper.
Paper 5: LogicSolver: Towards Interpretable Math Word Problem Solving with Logical Prompt-enhanced Learning
Findings of the Association for Computational Linguistics: EMNLP 2022
##Paper address: https:// arxiv.org/pdf/2205.08232.pdf
#In recent years, deep learning models have achieved great success in automatically solving mathematical application problems, especially in accurate answers. rate. However, because these models only use statistical clues (shallow heuristics) to achieve high solving performance and do not truly understand and reason about the mathematical logic behind the problem, these methods are difficult to explain.
In order to solve this problem and promote the development of the field of interpretable mathematical word problem solving, the Sun Yat-sen University Human-Machine Intelligence Integration Laboratory team constructed the first high-quality explained mathematical word problem data set, InterMWP. This data set contains 11,495 mathematical word problems and 210 logical formulas based on algebraic knowledge. The solution expression of each word problem is annotated with logical formulas. Different from existing mathematical application problem solving data sets, our InterMWP not only requires the problem solver to output the solving expression, but also requires the problem solver to output the logical expression based on algebraic knowledge corresponding to the solving expression, thereby realizing the model Explanation of the output. The similarities and differences between the InterMWP data set and other problem-solving data sets can be seen in Figure 8. For the specific annotation process, please refer to the original text.
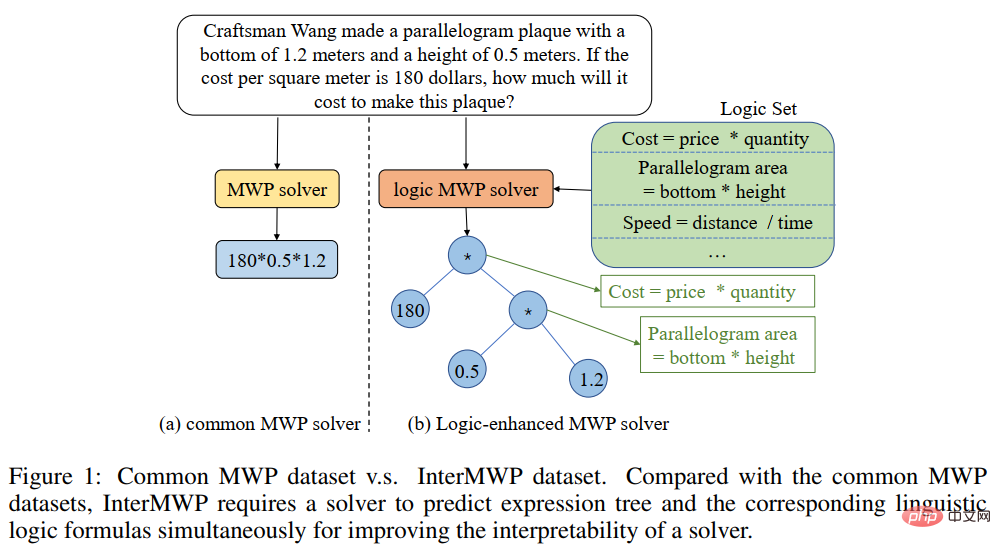
Figure 8 InterMWP dataset example
In order to utilize mathematical logic knowledge and empower the MWP problem solver with interpretability, our team further built a new mathematical application problem solving framework LogicSolver, as shown in Figure 9. This framework extracts relevant logical knowledge from the logical formula library as prompt information through retrieval, improving the semantic representation of the MWP by the question encoder and enhancing the generation ability of the logical explanation of the MWP.
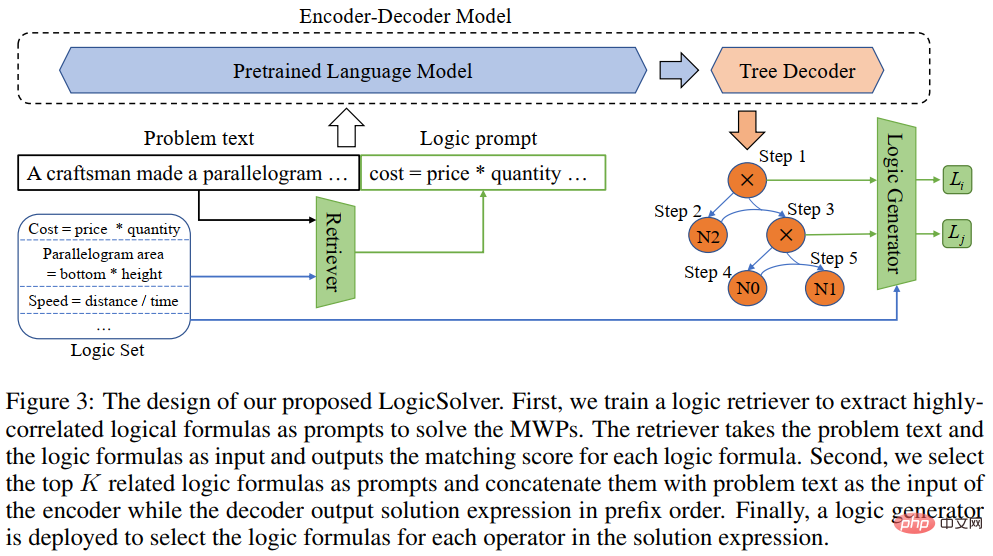
##Figure 9 LogicSolver design diagram
LogicSolver is mainly composed of three major components: a logical knowledge retrieval component, a logic prompt-enhanced MWP solver, and an explanation generation component. Logical knowledge retrieval component. For each MWP, we retrieve top-k highly relevant logical formulas from 210 logical formulas as hints to enhance the solution of MWP. We connect logical formula prompts with question text as input to drive the MWP model to generate solution expressions. Finally, to obtain explanations based on logical formulas, we deploy a logic generator to predict the logical formula corresponding to each internal node (i.e., operator) of the logical expression tree as the explanation for the solution.
In the experiments, we built multiple baseline models on the InterMWP dataset and compared our LogicSolver with these baseline models. The experimental results are shown in the table below.
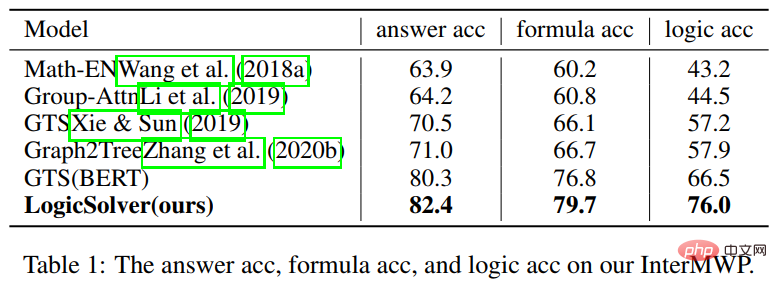
It can be seen from the experimental results that our LogicSolver can be improved in answer accuracy, formula accuracy, and logic formula accuracy. , indicating that our LogicSolver can have better logical interpretability (Logic Acc) while improving solution performance (Answer Acc and Formula Acc). For more research details, please refer to the original paper.
Paper 6: UniGeo: Unifying Geometry Logical Reasoning via Reformulating Mathematical Expression
Jiaqi Chen, Tong Li, Jinghui Qin, Pan Lu, Liang Lin, Chongyu Chen and Xiaodan Liang
The 2022 Conference on Empirical Methods in Natural Language Processing
#Automatic geometry problem solving is a benchmark for evaluating the multi-modal reasoning capabilities of deep models. However, in most existing work, automatic solution of geometric calculation problems and automatic proof of geometric problems are regarded as two different tasks, and different annotation processing is applied, which hinders the unified reasoning of deep models in different mathematical tasks. research progress. In essence, geometric calculation questions and geometric proof questions have similar problem expressions and the mathematical knowledge required to solve them also overlaps. Therefore, unified representation and learning of the two tasks of automatic solving of geometric calculation problems and automatic geometric problems can help improve the semantic understanding and symbolic reasoning of deep models for these two problems.
To this end, the Sun Yat-sen University Human-Machine-Object Intelligent Integration Laboratory team constructed a benchmark data set UniGeo that contains thousands of geometry questions. UniGeo includes 4,998 geometric calculation problems and 9,543 geometric proof problems. We provide multi-step proof annotations for each proof problem, and these annotations can be easily converted into executable symbolic programs. The calculation questions also use similar annotations, as shown in Figure 10. After annotation as shown in Figure 10, UniGeo can well represent geometric calculation problems and geometric proof problems in a formal symbolic language.
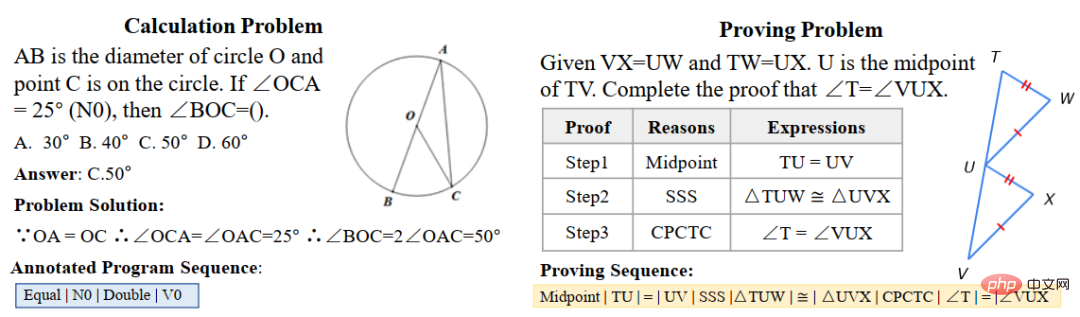
##Figure 10 UniGeo data sample
After using formal symbolic language to uniformly annotate geometric calculation questions and geometric proof questions, in order to verify that the unified representation of these two questions can effectively promote the model's semantic understanding and symbolic reasoning ability for geometric calculation questions and geometric proof questions, This enables more efficient solution of calculation problems and proof of proof problems. The Sun Yat-sen University Human-Machine-Object Intelligent Integration Laboratory team built Geoformer for unified processing of geometric problem solving and proof to handle geometric calculation problems and geometric proof problems at the same time, as shown in Figure 11.
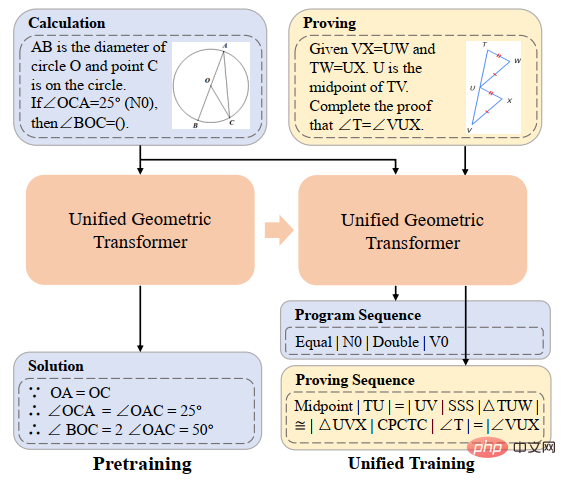
##Figure 11 GeoFormer diagram
In addition , In order to learn an efficient Geoformer to achieve unified geometric reasoning, the Sun Yat-sen University Human-Machine Intelligence Fusion Laboratory team further proposed a mathematical expression pre-training task, and combined the MLM task to perform task pre-training on the Geoformer, as shown in Figure 12.
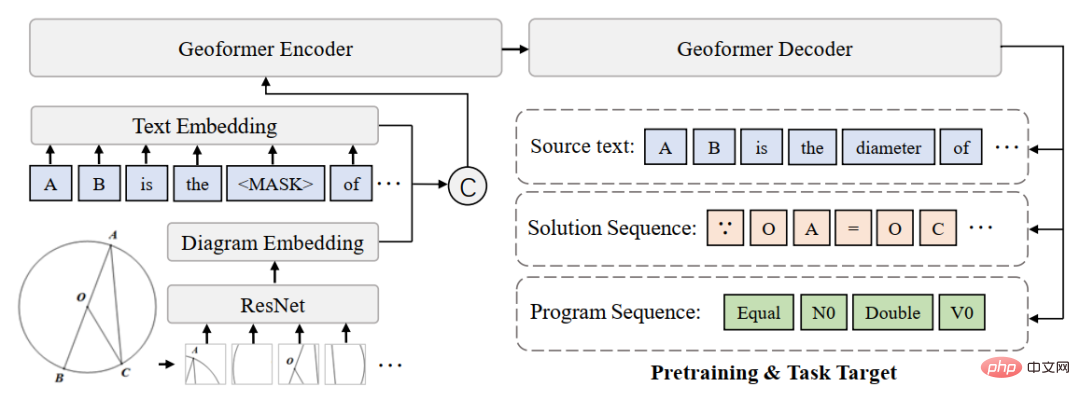
Figure 12 Schematic diagram of mathematical expression pre-training
In the experiment, we built multiple baseline models based on the UniGeo benchmark and compared the performance of our proposed GeoFormer. The experimental results are shown in the table below.
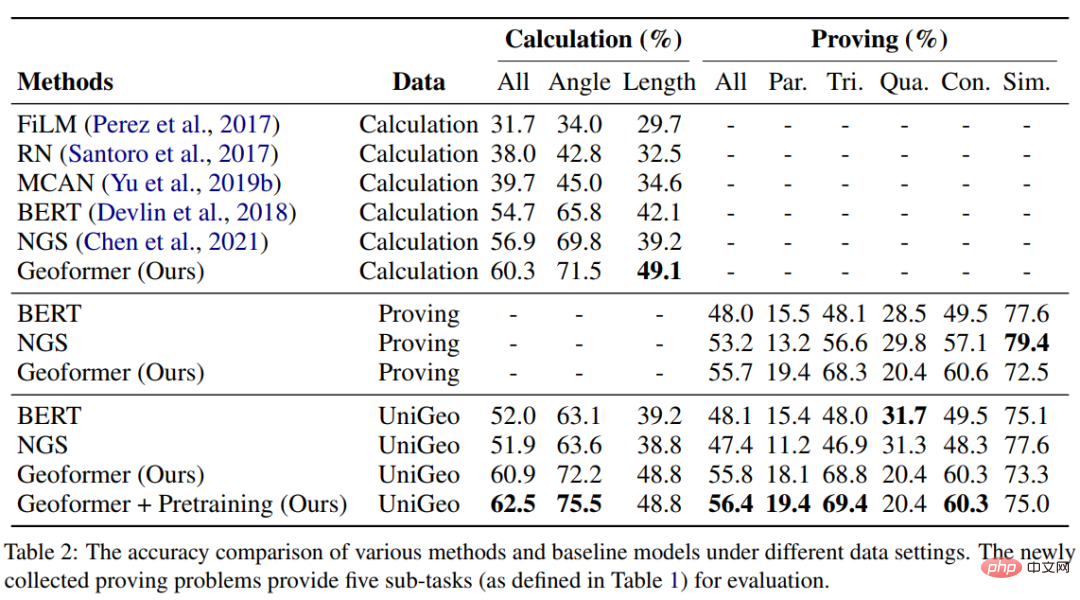
This work has been included by the main conference of EMNLP2022. Please stay tuned for more research details.
Paper 7: Template-based Contrastive Distillation Pre-training for Math Word Problem Solving
##Jinghui Qin*, Zhicheng Yang*, Jiaqi Chen, Xiaodan Liang and Liang LinAlthough deep learning models have made good progress in the field of mathematical problem solving, these models ignore The solution logic contained in the problem description, and this problem-solving logic can often correspond to the solution template (solution). As shown in Figure 13, two different word problems can each correspond to the same solution.
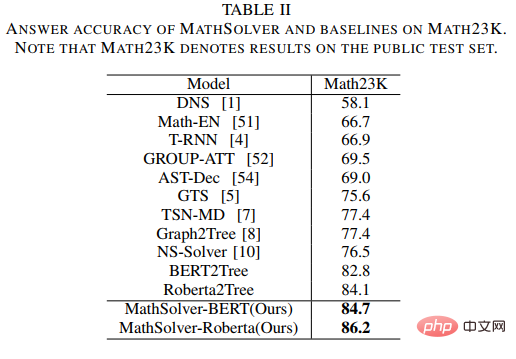
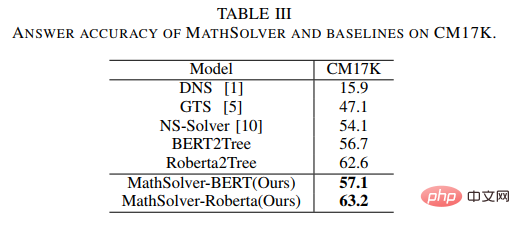
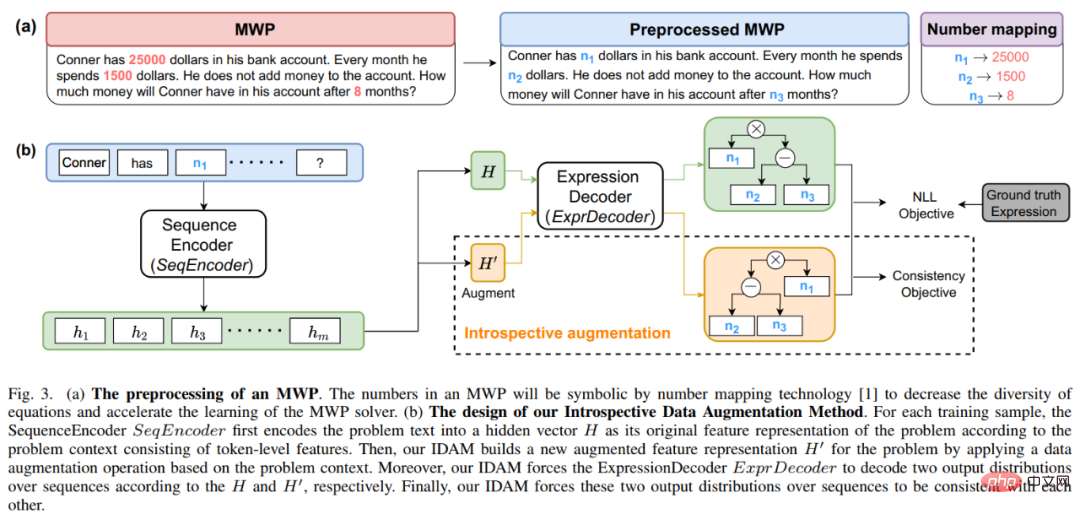
In addition, pre-trained language models (PLMs) contain rich knowledge and the ability to have high-quality semantic representations, which will be helpful for solving MWP problems. In order to make full use of the rich knowledge contained in the pre-trained language model and use solution logic to solve application problems more efficiently, the Sun Yat-sen University Human-Machine-Object Intelligent Integration Laboratory team proposed a solution template based on Comparison with pre-trained language models The distillation pre-training method performs domain pre-training on the problem encoder in the solver, as shown in Figure 14. This method uses multi-perspective contrastive learning to effectively consider mathematical logic knowledge while utilizing knowledge distillation to effectively retain the knowledge and high-quality semantic representation capabilities in the pre-trained language model. Specifically, we first use whether the solution templates between the two questions are consistent as an indicator to determine whether the two questions should be close to each other in the representation space. Then, we propose multi-perspective comparative learning, which involves comparative learning from teacher encoders, student encoders and their corresponding Momentum encoders, so that two question representations with the same solution template can interact with each other in the teacher representation space and the student representation space. Get close to achieve the injection of solution logic. In addition, in order to retain as much as possible the knowledge and high-quality representation capabilities contained in the student encoder initialized with a pre-trained language model, we use knowledge distillation to constrain the representation of the student encoder by using the feature representation of the teacher encoder as supervision To have the same representation capabilities as the trained teacher encoder, thereby achieving semantic preservation. ##Figure 14 Comparative distillation pre-training method based on solution template and pre-trained language model In the experiment, we use different pre-trained language models as initialization and verify the effect of our method. We initialize the problem encoder MathEncoder with BERT-base and Roberta-base weights respectively, and use the decoder in GTS as the expression decoder. We collectively refer to solvers based on MathEncoder as MathSolver. We compared MathSolver with multiple methods on Math23K and CM17K. The experimental results are shown in the table below. It can be seen from the experimental results that the method we proposed can effectively improve the solver's solution question ability, and can be applied on a variety of different pre-trained language models. The results have been submitted to IEEE Transactions on Neural Networks and Learning Systems, please stay tuned for more details. Paper 8: An Introspective Data Augmentation Method for Training Math Word Problem Solvers ##Jinghui Qin, Zhongzhan Huang, Ying Zeng, and Liang Lin The data bottleneck problem of MWP encourages us to think about how to use cost-effective data augmentation methods to improve data utilization efficiency and improve solver performance. The most direct data enhancement method is the data enhancement method based on input, such as commonly used character replacement, character deletion, etc. However, this type of method is not suitable for MWP, because MWP has the characteristics of conciseness and conciseness, which will disturb the input text. Or modification may make the meaning of the question unclear. In addition, the mathematical relationship contained in the meaning of the question cannot be changed, but this type of method is likely to change the mathematical relationship contained in the meaning of the question, as shown in Figure 15. Figure 15 Example of input-based data augmentation method not applicable to MWP tasks In addition, the Sun Yat-sen University Human-Machine-Object Intelligent Integration Laboratory team also conducted certain verification of the input-based data enhancement method. The experimental results are shown in Figure 16. Experimental results show that the input-based explicit data augmentation method is not applicable to the MWP task and cannot effectively alleviate the data bottleneck problem encountered by the MWP task. Figure 16 The input-based data enhancement method cannot improve the MWP problem-solving effect To this end, we propose a simple and efficient data enhancement method suitable for MWP data - the introspective data augmentation method (IDAM). During the training process, the representation of the question in the latent space is performed. Enhancement, thereby solving the problems encountered by input-based data enhancement methods in MWP solving tasks. The IDAM method performs different representation construction methods (mean pooling, hierarchical aggregation, random discarding, random exchange, etc.) by encoding the representation of the problem to obtain a new problem representation, and then uses the consistency objective function (based on the expression between JS divergence) to constrain the solver's expression decoding output based on the new problem representation to be consistent with the expression decoding output based on the original problem representation. A schematic diagram of the method is shown in Figure 17. ##Figure 17 Schematic diagram of the introspective data augmentation method (IDAM) In the experiment, we embedded IDAM into multiple SOTA methods and compared them on multiple data sets, verifying the effectiveness and versatility of our IDAM method. The experimental results are shown in the table below. It can be seen from the experimental results that under the same experimental configuration, our IDAM can improve the performance of different solver baseline models on different MWP data sets. This fully illustrates the effectiveness of our IDAM approach on the MWP problem. This result has been submitted to IEEE/ACM Transactions on Audio, Speech and Language Processing, please stay tuned for more details. Lab Introduction The Sun Yat-sen University Human-Computer-Cyber Intelligent Fusion Laboratory (HCP Lab) was founded in 2010 by Professor Lin Liang. The research topic on the layout of cutting-edge artificial intelligence technology has won the first prize of Science and Technology Award of China Image and Graphics Society, the Wu Wenjun Natural Science Award, the first prize of provincial natural science and other honors; it has trained national-level young talents such as Liang Xiaodan and Wang Keze.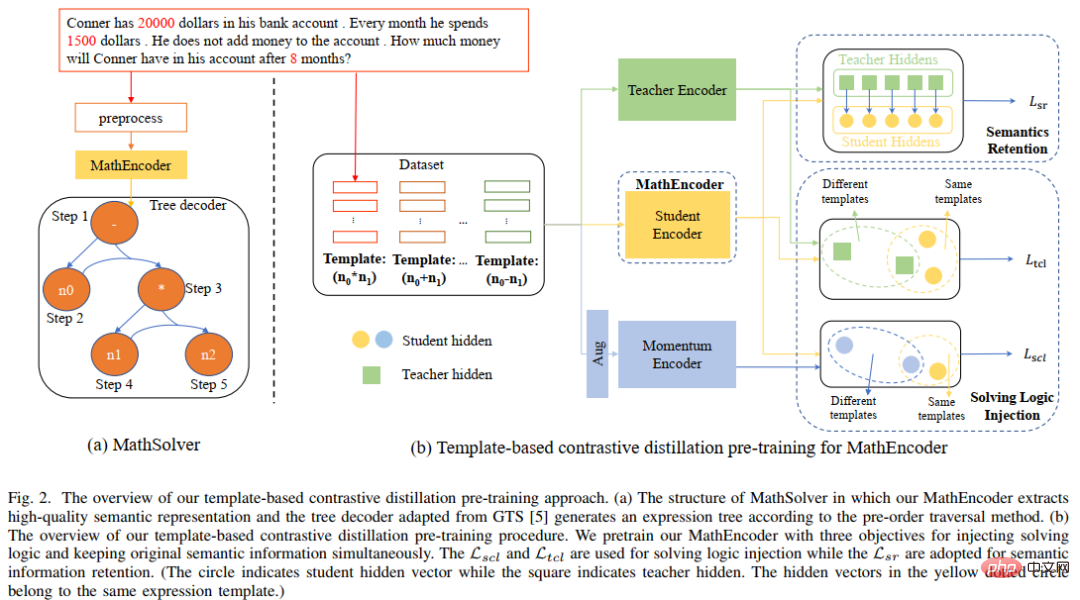 
The above is the detailed content of HCP Lab team of Sun Yat-sen University: New breakthroughs in AI problem-solving, neural networks open the door to mathematical reasoning. For more information, please follow other related articles on the PHP Chinese website!
What are the e-commerce platforms?
What is disk quota
Top ten digital currency exchanges
Introduction to dex concept digital currency
How to view stored procedures in MySQL
What drawing software are there?
The difference between static web pages and dynamic web pages
Introduction to laravel components
![[Web front-end] Node.js quick start](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
