 Technology peripherals
Technology peripherals
 AI
AI
 AI-driven operations research optimizes 'lithography machines'! The University of Science and Technology of China and others proposed a hierarchical sequence model to greatly improve the efficiency of mathematical programming solving.
AI-driven operations research optimizes 'lithography machines'! The University of Science and Technology of China and others proposed a hierarchical sequence model to greatly improve the efficiency of mathematical programming solving.
AI-driven operations research optimizes 'lithography machines'! The University of Science and Technology of China and others proposed a hierarchical sequence model to greatly improve the efficiency of mathematical programming solving.
The mathematical programming solver is known as the "lithography machine" in the field of operations research and optimization due to its importance and versatility.
Among them, Mixed-Integer Linear Programming (MILP) is a key component of the mathematical programming solver and can model a large number of practical applications, such as industrial production scheduling, logistics scheduling, chip design, and path planning. , financial investment and other major areas.
Recently, Professor Wang Jie’s team at the MIRA Lab of the University of Science and Technology of China and Huawei’s Noah’s Ark Laboratory jointly proposed the Hierarchical Sequence Model (HEM), which greatly improves the solving efficiency of the mixed integer linear programming solver, and related results were published At ICLR 2023.
Currently, the algorithm has been integrated into Huawei’s MindSpore ModelZoo model library, and related technologies and capabilities will be integrated into Huawei’s OptVerse AI solver within this year. This solver aims to combine operations research and AI to break through the industry's operational research optimization limits, assist enterprises in quantitative decision-making and refined operations, and achieve cost reduction and efficiency improvement!

Author list: Wang Zhihai*, Li Xijun*, Wang Jie**, Kuang Yufei, Yuan Mingxuan, Zeng Jia, Zhang Yongdong, Wu Feng
Paper link: https://openreview.net/forum?id=Zob4P9bRNcK
Open source data set: https://drive.google.com/drive/folders/1LXLZ8vq3L7v00XH-Tx3U6hiTJ79sCzxY?usp=sharing
PyTorch version open source code: https://github.com/MIRALab-USTC/L2O-HEM-Torch
MindSpore version open source code: https://gitee.com/mindspore/models/ tree/master/research/l2o/hem-learning-to-cut
Tianchiou (OptVerse) AI solver: https://www.huaweicloud.com/product/modelarts/optverse.html
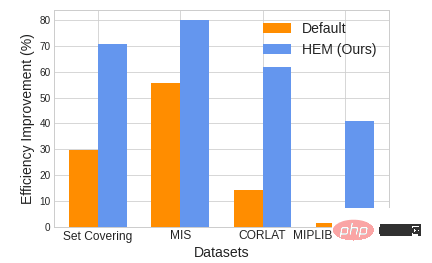
Figure 1. Comparison of solution efficiency between HEM and solver default strategy (Default). HEM solution efficiency can be improved by up to 47.28%
1 Introduction
Cutting planes (cuts) are crucial for efficiently solving mixed integer linear programming problems.
The cutting plane selection (cut selection) aims to select an appropriate subset of the cutting planes to be selected to improve the efficiency of solving MILP. Cutting plane selection depends heavily on two sub-problems: (P1) which cutting planes should be preferred, and (P2) how many cutting planes should be selected.
Although many modern MILP solvers handle (P1) and (P2) through manually designed heuristics, machine learning methods have the potential to learn more efficient heuristics.
However, many existing learning methods focus on learning which cutting planes should be prioritized, but ignore learning how many cutting planes should be selected. In addition, we have observed from a large number of experimental results that another sub-problem, namely (P3), which cutting plane order should be preferred, also has a significant impact on the efficiency of solving MILP.
To address these challenges, we propose a novel Hierarchical Sequence Model (HEM) and learn the cutting plane selection strategy through a reinforcement learning framework.
As far as we know, HEM is the first learning method that can handle (P1), (P2) and (P3) simultaneously. Experiments show that HEM significantly improves the efficiency of solving MILP compared to manually designed and learned baselines on artificially generated and large-scale real-world MILP datasets.
2 Background and problem introduction
2.1 Introduction to cutting planes (cuts)
Mixed-Integer Linear Programming (MILP) is a It is a general optimization model widely used in various practical application fields, such as supply chain management [1], production planning [2], planning and dispatching [3], factory location selection [4], packing problem [5], etc.
The standard MILP has the following form:
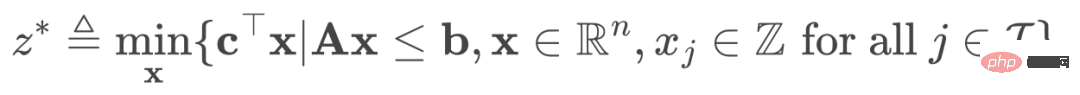
(1)
Given the problem ( 1), we discard all its integer constraints and obtain the linear programming relaxation (LPR) problem, which is in the form:
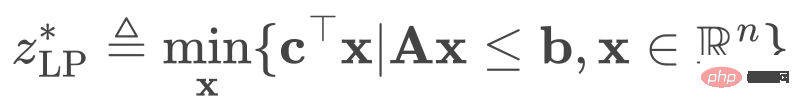
(2)
Since problem (2) extends the feasible set of problem (1), we can have that the optimal value of the LPR problem is the lower bound of the original MILP problem.
Given the LPR problem in (2), cutting planes (cuts) are a class of legal linear inequalities that, after being added to the linear programming relaxation problem, can shrink the feasibility of the LPR problem domain space without removing any integer feasible solutions of the original MILP problem.
2.2 Introduction to cut selection
The MILP solver can generate a large number of cutting planes during the process of solving the MILP problem, and will continue to add cutting planes to the original problem in successive rounds.
Specifically, each round includes five steps:
(1) Solve the current LPR problem;
(2) Generate a series of cutting planes to be selected ;
(3) Select a suitable subset from the cutting plane to be selected;
(4) Add the selected subset to the LPR problem in (1) to get a New LPR problem;
(5) The cycle is repeated and based on the new LPR problem, enter the next round.
Adding all generated cutting planes to the LPR problem shrinks the feasible region space of the problem to the maximum extent possible to maximize the lower bound.
However, adding too many cutting planes may cause the problem to have too many constraints, increase the computational overhead of problem solving and cause numerical instability problems [6,7].
Therefore, researchers have proposed cutting plane selection (cut selection), which aims to select an appropriate subset of candidate cutting planes to improve the efficiency of MILP problem solving as much as possible. Cutting plane selection is crucial to improve the efficiency of solving mixed integer linear programming problems [8, 9, 10].
2.3 Heuristic experiment - cutting plane addition order
We designed two cutting plane selection heuristic algorithms, namely RandomAll and RandomNV (see Chapter 3 of the original paper for details).
They all add the selected cuts to the MILP problem in random order after selecting a batch of cuts. As shown in the results in Figure 2, when the same cutting plane is selected, adding these selected cutting planes in different orders has a great impact on the solving efficiency of the solver (see Chapter 3 of the original paper for detailed result analysis).
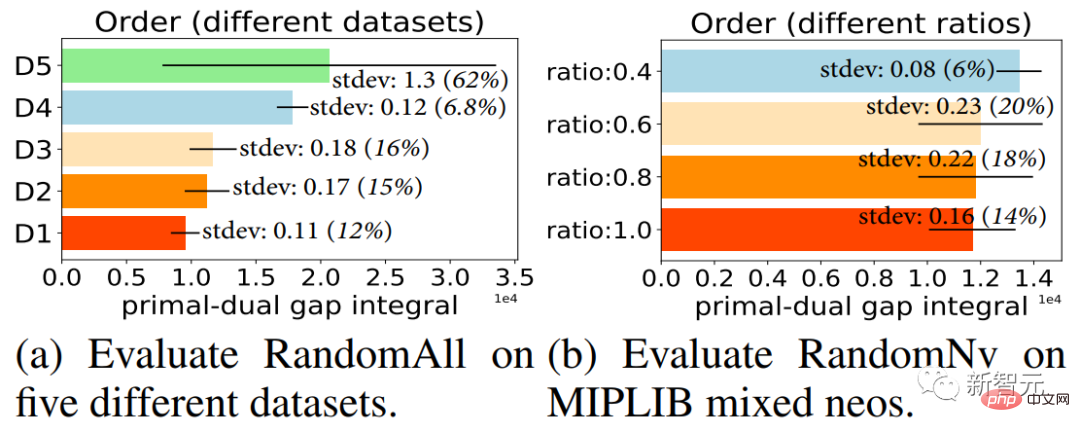
Figure 2. Each column represents the same batch of cutting planes selected in the solver, and these are added in 10 rounds in different orders. The cutting plane is selected, the mean value of the solver's final solution efficiency, and the standard deviation line in the column represents the standard deviation of the solution efficiency under different orders. The larger the standard deviation, the greater the impact of order on the solving efficiency of the solver.
3 Method Introduction
In the cutting plane selection task, the optimal subset that should be selected cannot be obtained in advance.
However, we can use the solver to evaluate the quality of any selected subset and use this evaluation as feedback to the learning algorithm.
Therefore, we use the Reinforcement Learning (RL) paradigm to learn the cutting plane selection strategy through trial and error.
In this section, we elaborate on our proposed RL framework.
First, we model the cutting plane selection task as a Markov Decision Process (MDP); then, we introduce our proposed hierarchical sequence model (HEM) in detail; Finally, we derive hierarchical policy gradients that can efficiently train HEM. Our overall RL framework diagram is shown in Figure 3.
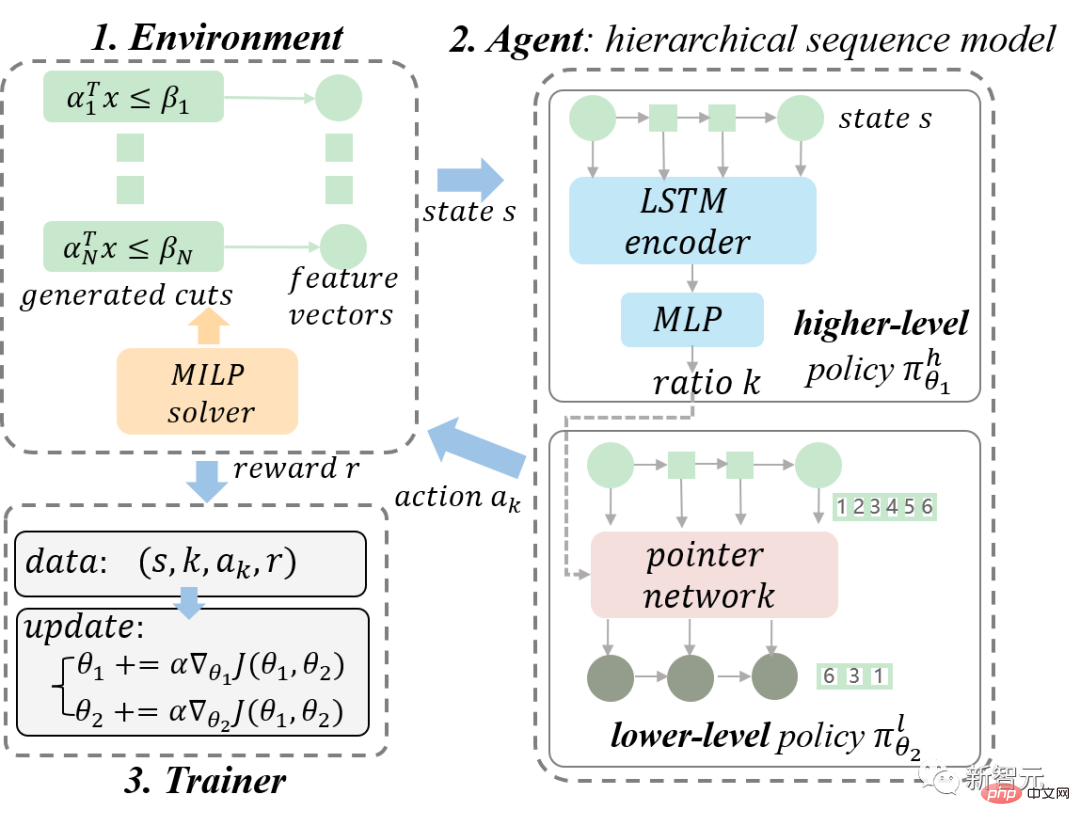
Figure 3. Diagram of our proposed overall RL framework. We model the MILP solver as the environment and the HEM model as the agent. We collect training data through continuous interaction between the agent and the environment, and train the HEM model using hierarchical policy gradient.
3.1 Problem Modeling
State space: Since the current LP relaxation and the generated candidate cuts contain the core information of cutting plane selection, we define the state. Here represents the mathematical model of the current LP relaxation, represents the set of candidate cutting planes, and represents the optimal solution of LP relaxation. In order to encode state information, we design 13 features for each candidate cutting plane based on the information. That is, we represent the state s through a 13-dimensional feature vector. Please see Chapter 4 of the original article for specific details.
Action space: In order to consider both the proportion and order of the selected cuts, we define the action space as all ordered subsets of the set of candidate cuts.
Reward function: In order to evaluate the impact of adding cut on solving MILP, we can use solution time, primal-dual gap integral, and dual bound improvement. Please see Chapter 4 of the original article for specific details.
Transition function: The transfer function outputs the next state given the current state and the action taken. The transfer function in the cutting plane selection task is implicitly provided by the solver.
For more modeling details, please see Chapter 4 of the original article.
3.2 Strategy Model: Hierarchical Sequence Model
As shown in Figure 3, we model the MILP solver as the environment and the HEM as the agent. The proposed method is introduced in detail below. HEM model. In order to facilitate reading, we simplify the motivation of the method and focus on clearly explaining the method implementation. Interested readers are welcome to refer to Chapter 4 of the original paper for relevant details.
As shown in the Agent module in Figure 3, HEM consists of upper and lower policy models. The upper and lower layer models learn the upper layer policy (policy) and the lower layer policy respectively.
First, the upper-level policy learns the number of cuts that should be selected by predicting the appropriate proportions. Assuming that the state length is and the prediction ratio is , then the number of cuts that should be selected for prediction is 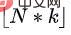
, where 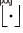 represents the rounding down function. We define
represents the rounding down function. We define  .
.
Secondly, the lower-level policy learns to select an ordered subset of a given size. The lower-level policy can define 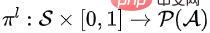 , where
, where 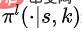 represents the probability distribution on the action space given the state S and the proportion K. Specifically, we model the underlying policy as a sequence to sequence model (sequence model).
represents the probability distribution on the action space given the state S and the proportion K. Specifically, we model the underlying policy as a sequence to sequence model (sequence model).
Finally, the cut selection strategy is derived through the law of total probability, that is,
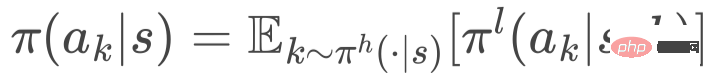
3.3 Training method: hierarchical strategy gradient
Given optimization objective function
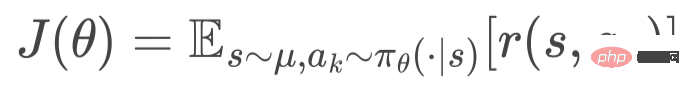
Figure 4. Hierarchical policy gradient. We optimize the HEM model in this stochastic gradient descent manner.
4 Experiment Introduction
Our experiment has five main parts:
Experiment 1. On 3 artificially generated MILP problems and 6 problems with Our method is evaluated on the challenging MILP problem benchmark.
Experiment 2. Conduct carefully designed ablation experiments to provide in-depth insights into HEM.
Experiment 3. Test the generalization performance of HEM for problem size.
Experiment 4. Visualize the characteristics of the cutting planes selected by our method and the baseline.
Experiment 5. Deploy our method to Huawei's actual production scheduling problem to verify the superiority of HEM.
We only introduce Experiment 1 in this article. For more experimental results, please see Chapter 5 of the original paper. Please note that all experimental results reported in our paper are results obtained based on training with the PyTorch version code.
The results of Experiment 1 are shown in Table 1. We compared the results of HEM and 6 baselines on 9 open source data sets. Experimental results show that HEM can improve solving efficiency by about 20% on average.
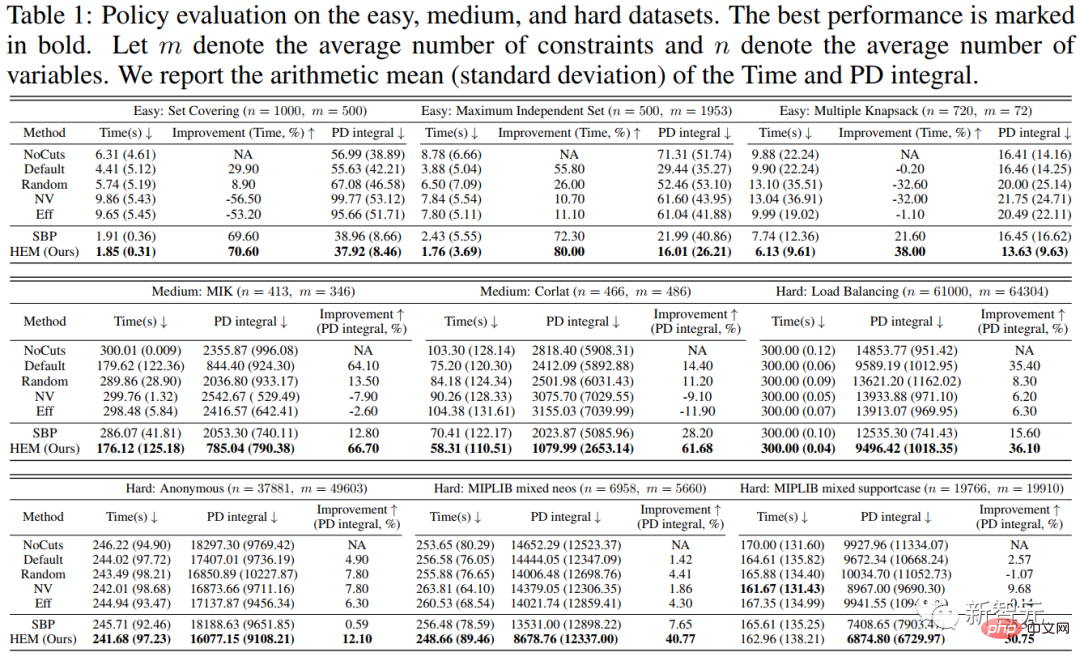
Figure 5. Strategy evaluation on easy, medium and hard datasets. Optimum performance is marked in bold. Let m represent the average number of constraints, and n represent the average number of variables. We show the arithmetic mean (standard deviation) of solution times and primal-dual gap integrals.
The above is the detailed content of AI-driven operations research optimizes 'lithography machines'! The University of Science and Technology of China and others proposed a hierarchical sequence model to greatly improve the efficiency of mathematical programming solving.. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1359
1359
 52
52
 How to use PS feathering to create transparent effects?
Apr 06, 2025 pm 07:03 PM
How to use PS feathering to create transparent effects?
Apr 06, 2025 pm 07:03 PM
Transparent effect production method: Use selection tool and feathering to cooperate: select transparent areas and feathering to soften edges; change the layer blending mode and opacity to control transparency. Use masks and feathers: select and feather areas; add layer masks, and grayscale gradient control transparency.
 How is the compatibility of Bootstrap image centering
Apr 07, 2025 am 07:51 AM
How is the compatibility of Bootstrap image centering
Apr 07, 2025 am 07:51 AM
Bootstrap image centering faces compatibility issues. The solution is as follows: Use mx-auto to center the image horizontally for display: block. Vertical centering Use Flexbox or Grid layouts to ensure that the parent element is vertically centered to align the child elements. For IE browser compatibility, use tools such as Autoprefixer to automatically add browser prefixes. Optimize image size, format and loading order to improve page performance.
 How to change the size of a Bootstrap list?
Apr 07, 2025 am 10:45 AM
How to change the size of a Bootstrap list?
Apr 07, 2025 am 10:45 AM
The size of a Bootstrap list depends on the size of the container that contains the list, not the list itself. Using Bootstrap's grid system or Flexbox can control the size of the container, thereby indirectly resizing the list items.
 What should I do if the PS card is in the loading interface?
Apr 06, 2025 pm 06:54 PM
What should I do if the PS card is in the loading interface?
Apr 06, 2025 pm 06:54 PM
The loading interface of PS card may be caused by the software itself (file corruption or plug-in conflict), system environment (due driver or system files corruption), or hardware (hard disk corruption or memory stick failure). First check whether the computer resources are sufficient, close the background program and release memory and CPU resources. Fix PS installation or check for compatibility issues for plug-ins. Update or fallback to the PS version. Check the graphics card driver and update it, and run the system file check. If you troubleshoot the above problems, you can try hard disk detection and memory testing.
 How to add icons to Bootstrap list?
Apr 07, 2025 am 10:42 AM
How to add icons to Bootstrap list?
Apr 07, 2025 am 10:42 AM
How to add icons to the Bootstrap list: directly stuff the icon into the list item <li>, using the class name provided by the icon library (such as Font Awesome). Use the Bootstrap class to align icons and text (for example, d-flex, justify-content-between, align-items-center). Use the Bootstrap tag component (badge) to display numbers or status. Adjust the icon position (flex-direction: row-reverse;), control the style (CSS style). Common error: The icon does not display (not
 How to implement nesting of Bootstrap lists?
Apr 07, 2025 am 10:27 AM
How to implement nesting of Bootstrap lists?
Apr 07, 2025 am 10:27 AM
Nested lists in Bootstrap require the use of Bootstrap's grid system to control the style. First, use the outer layer <ul> and <li> to create a list, then wrap the inner layer list in <div class="row> and add <div class="col-md-6"> to the inner layer list to specify that the inner layer list occupies half the width of a row. In this way, the inner list can have the right one
 What method is used to convert strings into objects in Vue.js?
Apr 07, 2025 pm 09:39 PM
What method is used to convert strings into objects in Vue.js?
Apr 07, 2025 pm 09:39 PM
When converting strings to objects in Vue.js, JSON.parse() is preferred for standard JSON strings. For non-standard JSON strings, the string can be processed by using regular expressions and reduce methods according to the format or decoded URL-encoded. Select the appropriate method according to the string format and pay attention to security and encoding issues to avoid bugs.
 What changes have been made with the list style of Bootstrap 5?
Apr 07, 2025 am 11:09 AM
What changes have been made with the list style of Bootstrap 5?
Apr 07, 2025 am 11:09 AM
Bootstrap 5 list style changes are mainly due to detail optimization and semantic improvement, including: the default margins of unordered lists are simplified, and the visual effects are cleaner and neat; the list style emphasizes semantics, enhancing accessibility and maintainability.



