Optimal transportation and its application to fairness
Translator | Li Rui
Reviewer | Sun Shujuan
Optimal transportation originated from economics and is now developed as a tool for how to best allocate resources. The origins of optimal transportation theory can be traced back to 1781, when French scientist Gaspard Monge studied a method of purportedly "moving the earth" and building fortifications for Napoleon's army. Overall, optimal transportation is the problem of how to move all resources (such as iron ore) from a set of starting points (mines) to a set of end points (steel plants) while minimizing the total distance the resources must travel. Mathematically, the researchers wanted to find a function that maps each origin to a destination while minimizing the total distance between the origin and its corresponding destination. Despite its innocuous description, progress on the original conception of the problem, known as Munger's conception, stalled for nearly 200 years.
In the 1940s, Soviet mathematician Leonid Kantorovich adapted the formulation of the problem into a modern version, now known as Monge Kantorov's theory, which was the first step toward a solution. The novelty here is allowing some iron ore from the same mine to be supplied to different steel plants. For example, 60% of the iron ore from a mine can be provided to a steel plant, while the remaining 40% of the iron ore from the mine can be provided to another steel plant. Mathematically, this is no longer a function, as the same origin now maps to potentially multiple destinations. In contrast, this is known as the coupling between the origin distribution and the destination distribution, as shown in the figure below; selecting a mine from the blue distribution (origin) and moving vertically along the figure shows where the iron ore is sent Distribution of steel plants (destination).
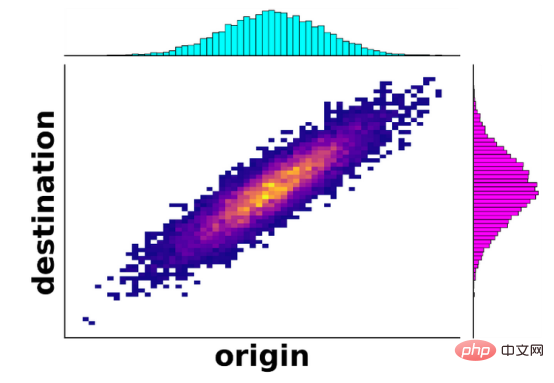
As part of this new development, Kantorivich introduced an important concept called the Wasserstein distance. Similar to the distance between two points on a map, the Wasserstein distance (also known as the bulldozer distance inspired by its original scenario) measures the distance between two distributions, such as the blue and magenta distributions in this case. If all iron mines are far from all iron plants, then the Wasserstein distance between the distribution (location) of mines and the distribution of steel plants will be large. Even with these new improvements, it's still unclear whether there really is a best way to transport iron ore resources, let alone which method. Finally, in the 1990s, the theory began to develop rapidly as improvements in mathematical analysis and optimization led to partial solutions to the problem. In the 21st century, optimal transportation began to spread to other fields, such as particle physics, fluid dynamics, and even statistics and machine learning.
Optimal Transportation in Modern Times
With the explosion of new theories, optimal transportation has become the center of many new statistical and artificial intelligence algorithms over the past two decades. In almost every statistical algorithm, data are modeled, explicitly or implicitly, as having some underlying probability distribution. For example, if data on individual income are collected in different countries, there will be a probability distribution of that population's income in each country. If you wish to compare two countries based on the income distribution of their population, you need a way to measure the gap between the two distributions. This is exactly why optimizing transportation (especially Wasserstein distance) becomes so useful in data science. However, Wasserstein distance is not the only measure of the distance between two probability distributions. In fact, due to their connection to physics and information theory, the two options L-2 distance and Kullback-Leibler (KL) divergence have historically been more common. The main advantage of Wasserstein distance over these alternatives is that it takes into account both the values and their probabilities when calculating the distance, whereas L-2 distance and KL divergence only take into account probabilities. The image below shows an example of an artificial dataset on income for three fictional countries.
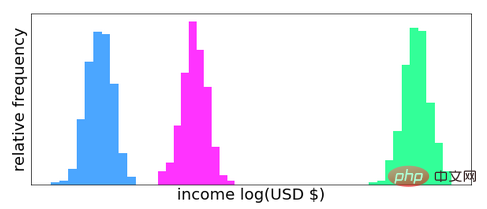
In this case, since the distributions do not overlap, the L-2 distance (or KL divergence) between the blue and magenta distributions will be the same as the blue and magenta distributions The L-2 distance between green distributions is roughly the same. On the other hand, the Wasserstein distance between the blue and magenta distributions will be much smaller than the Wasserstein distance between the blue and green distributions because there is a significant difference between the values (horizontal separation). This property of Wasserstein distance makes it ideal for quantifying differences between distributions, especially differences between data sets.
Achieving Fairness with Optimal Transport
With massive amounts of data being collected every day and machine learning becoming more common in many industries, data scientists must be increasingly careful not to let them Analytics and algorithms perpetuate existing biases and biases in the data. For example, if a home mortgage approval data set contains information about the race of applicants, but minorities were discriminated against in the collection process due to the methods used or unconscious bias, then a model trained on that data will reflect the underlying deviation.
Optimizing transportation can help mitigate this bias and improve fairness in two ways. The first and simplest method is to use Wasserstein distance to determine whether there is potential bias in the data set. For example, one can estimate the Wasserstein distance between the distribution of loan amounts approved for women and the distribution of loan amounts approved for men. If the Wasserstein distance is very large, that is, statistically significant, then a potential bias may be suspected. This idea of testing whether there is a difference between two groups is known in statistics as a two-sample hypothesis test.
Alternatively, optimal shipping can even be used to enforce fairness in the model when the underlying dataset itself is biased. This is useful from a practical perspective, as many real-world datasets exhibit some degree of bias, and collecting unbiased data can be very expensive, time-consuming, or unfeasible. Therefore, it is more practical to use existing data, no matter how imperfect, and try to ensure that the model mitigates this bias. This is accomplished by enforcing a constraint in the model called strong demographic parity, which forces model predictions to be statistically independent of any sensitive attributes. One approach is to map the distribution of model predictions to the distribution of adjusted predictions that do not depend on sensitive attributes. However, adjusting predictions also changes the performance and accuracy of the model, so there is a trade-off between model performance and the degree to which the model relies on sensitive attributes (i.e., fairness).
Achieve optimal shipping by changing predictions as little as possible to ensure optimal model performance, while still ensuring that new predictions are independent of sensitive attributes. The new distribution predicted by this adjusted model is called the Wasserstein centroid and has been the subject of much research over the past decade. The Wasserstein center of gravity is similar to the mean of a probability distribution in that it minimizes the total distance from itself to all other distributions. The image below shows three distributions (green, blue and magenta) along with their Wasserstein centers of gravity (red).
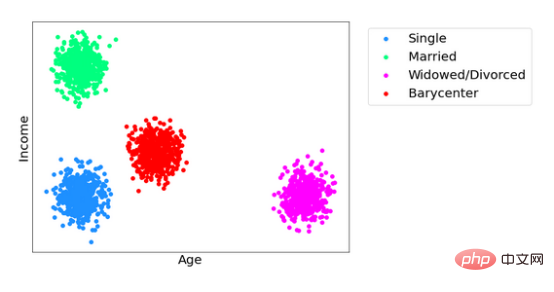
In the above example, suppose a model is built to predict someone's age and income based on a dataset that contains a sensitive attribute, such as marital status. There are three possible values: single (blue), married (green), and widowed/divorced (magenta). The scatter plot shows the distribution of model predictions for each different value. But wishing to adjust these values so that the predictions of the new model are blind to a person's marital status, each of these distributions can be mapped to the center of gravity in red using optimal transport. Because all values map to the same distribution, one can no longer judge a person's marital status based on income and age, or vice versa. The center of gravity preserves the fidelity of the model as much as possible.
The increasing ubiquity of data and machine learning models used in business and government decision-making has led to the emergence of new social and ethical questions about how to ensure the fair application of these models. Many datasets contain some kind of bias due to the nature of how they are collected, so it is important that models trained on them do not exacerbate this bias or any historical discrimination. Optimal transportation is just one way to solve this problem, which has been growing in recent years. Nowadays, there are fast and efficient ways to calculate optimal transportation maps and distances, making this approach suitable for modern large data sets. As people increasingly rely on data-based models and insights, fairness has and will continue to be a core issue in data science, and optimal transportation will play a key role in achieving this goal.
Original title: Optimal Transport and its Applications to Fairness, author: Terrence Alsup
The above is the detailed content of Optimal transportation and its application to fairness. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1382
1382
 52
52
 Bytedance Cutting launches SVIP super membership: 499 yuan for continuous annual subscription, providing a variety of AI functions
Jun 28, 2024 am 03:51 AM
Bytedance Cutting launches SVIP super membership: 499 yuan for continuous annual subscription, providing a variety of AI functions
Jun 28, 2024 am 03:51 AM
This site reported on June 27 that Jianying is a video editing software developed by FaceMeng Technology, a subsidiary of ByteDance. It relies on the Douyin platform and basically produces short video content for users of the platform. It is compatible with iOS, Android, and Windows. , MacOS and other operating systems. Jianying officially announced the upgrade of its membership system and launched a new SVIP, which includes a variety of AI black technologies, such as intelligent translation, intelligent highlighting, intelligent packaging, digital human synthesis, etc. In terms of price, the monthly fee for clipping SVIP is 79 yuan, the annual fee is 599 yuan (note on this site: equivalent to 49.9 yuan per month), the continuous monthly subscription is 59 yuan per month, and the continuous annual subscription is 499 yuan per year (equivalent to 41.6 yuan per month) . In addition, the cut official also stated that in order to improve the user experience, those who have subscribed to the original VIP
 Context-augmented AI coding assistant using Rag and Sem-Rag
Jun 10, 2024 am 11:08 AM
Context-augmented AI coding assistant using Rag and Sem-Rag
Jun 10, 2024 am 11:08 AM
Improve developer productivity, efficiency, and accuracy by incorporating retrieval-enhanced generation and semantic memory into AI coding assistants. Translated from EnhancingAICodingAssistantswithContextUsingRAGandSEM-RAG, author JanakiramMSV. While basic AI programming assistants are naturally helpful, they often fail to provide the most relevant and correct code suggestions because they rely on a general understanding of the software language and the most common patterns of writing software. The code generated by these coding assistants is suitable for solving the problems they are responsible for solving, but often does not conform to the coding standards, conventions and styles of the individual teams. This often results in suggestions that need to be modified or refined in order for the code to be accepted into the application
 Can fine-tuning really allow LLM to learn new things: introducing new knowledge may make the model produce more hallucinations
Jun 11, 2024 pm 03:57 PM
Can fine-tuning really allow LLM to learn new things: introducing new knowledge may make the model produce more hallucinations
Jun 11, 2024 pm 03:57 PM
Large Language Models (LLMs) are trained on huge text databases, where they acquire large amounts of real-world knowledge. This knowledge is embedded into their parameters and can then be used when needed. The knowledge of these models is "reified" at the end of training. At the end of pre-training, the model actually stops learning. Align or fine-tune the model to learn how to leverage this knowledge and respond more naturally to user questions. But sometimes model knowledge is not enough, and although the model can access external content through RAG, it is considered beneficial to adapt the model to new domains through fine-tuning. This fine-tuning is performed using input from human annotators or other LLM creations, where the model encounters additional real-world knowledge and integrates it
 Seven Cool GenAI & LLM Technical Interview Questions
Jun 07, 2024 am 10:06 AM
Seven Cool GenAI & LLM Technical Interview Questions
Jun 07, 2024 am 10:06 AM
To learn more about AIGC, please visit: 51CTOAI.x Community https://www.51cto.com/aigc/Translator|Jingyan Reviewer|Chonglou is different from the traditional question bank that can be seen everywhere on the Internet. These questions It requires thinking outside the box. Large Language Models (LLMs) are increasingly important in the fields of data science, generative artificial intelligence (GenAI), and artificial intelligence. These complex algorithms enhance human skills and drive efficiency and innovation in many industries, becoming the key for companies to remain competitive. LLM has a wide range of applications. It can be used in fields such as natural language processing, text generation, speech recognition and recommendation systems. By learning from large amounts of data, LLM is able to generate text
 Five schools of machine learning you don't know about
Jun 05, 2024 pm 08:51 PM
Five schools of machine learning you don't know about
Jun 05, 2024 pm 08:51 PM
Machine learning is an important branch of artificial intelligence that gives computers the ability to learn from data and improve their capabilities without being explicitly programmed. Machine learning has a wide range of applications in various fields, from image recognition and natural language processing to recommendation systems and fraud detection, and it is changing the way we live. There are many different methods and theories in the field of machine learning, among which the five most influential methods are called the "Five Schools of Machine Learning". The five major schools are the symbolic school, the connectionist school, the evolutionary school, the Bayesian school and the analogy school. 1. Symbolism, also known as symbolism, emphasizes the use of symbols for logical reasoning and expression of knowledge. This school of thought believes that learning is a process of reverse deduction, through existing
 To provide a new scientific and complex question answering benchmark and evaluation system for large models, UNSW, Argonne, University of Chicago and other institutions jointly launched the SciQAG framework
Jul 25, 2024 am 06:42 AM
To provide a new scientific and complex question answering benchmark and evaluation system for large models, UNSW, Argonne, University of Chicago and other institutions jointly launched the SciQAG framework
Jul 25, 2024 am 06:42 AM
Editor |ScienceAI Question Answering (QA) data set plays a vital role in promoting natural language processing (NLP) research. High-quality QA data sets can not only be used to fine-tune models, but also effectively evaluate the capabilities of large language models (LLM), especially the ability to understand and reason about scientific knowledge. Although there are currently many scientific QA data sets covering medicine, chemistry, biology and other fields, these data sets still have some shortcomings. First, the data form is relatively simple, most of which are multiple-choice questions. They are easy to evaluate, but limit the model's answer selection range and cannot fully test the model's ability to answer scientific questions. In contrast, open-ended Q&A
 SOTA performance, Xiamen multi-modal protein-ligand affinity prediction AI method, combines molecular surface information for the first time
Jul 17, 2024 pm 06:37 PM
SOTA performance, Xiamen multi-modal protein-ligand affinity prediction AI method, combines molecular surface information for the first time
Jul 17, 2024 pm 06:37 PM
Editor | KX In the field of drug research and development, accurately and effectively predicting the binding affinity of proteins and ligands is crucial for drug screening and optimization. However, current studies do not take into account the important role of molecular surface information in protein-ligand interactions. Based on this, researchers from Xiamen University proposed a novel multi-modal feature extraction (MFE) framework, which for the first time combines information on protein surface, 3D structure and sequence, and uses a cross-attention mechanism to compare different modalities. feature alignment. Experimental results demonstrate that this method achieves state-of-the-art performance in predicting protein-ligand binding affinities. Furthermore, ablation studies demonstrate the effectiveness and necessity of protein surface information and multimodal feature alignment within this framework. Related research begins with "S
 SK Hynix will display new AI-related products on August 6: 12-layer HBM3E, 321-high NAND, etc.
Aug 01, 2024 pm 09:40 PM
SK Hynix will display new AI-related products on August 6: 12-layer HBM3E, 321-high NAND, etc.
Aug 01, 2024 pm 09:40 PM
According to news from this site on August 1, SK Hynix released a blog post today (August 1), announcing that it will attend the Global Semiconductor Memory Summit FMS2024 to be held in Santa Clara, California, USA from August 6 to 8, showcasing many new technologies. generation product. Introduction to the Future Memory and Storage Summit (FutureMemoryandStorage), formerly the Flash Memory Summit (FlashMemorySummit) mainly for NAND suppliers, in the context of increasing attention to artificial intelligence technology, this year was renamed the Future Memory and Storage Summit (FutureMemoryandStorage) to invite DRAM and storage vendors and many more players. New product SK hynix launched last year




