 Technology peripherals
Technology peripherals
 AI
AI
 Animation production efficiency increased by 80%! This AI software realizes high-precision video motion capture with one click
Animation production efficiency increased by 80%! This AI software realizes high-precision video motion capture with one click
Animation production efficiency increased by 80%! This AI software realizes high-precision video motion capture with one click
AIGC has a new magic!
No need for animators' hand K, habit capture or light capture, just provide a video, this AI motion capture software can automatically output the action. In just a few minutes, the animation of the virtual human is completed.

Not only the large-frame movements of the limbs, but also the details of the hands can be accurately captured.
In addition to single-view video, it can also support multiple-view videos. Compared with other motion capture software that only supports monocular recognition, this software can provide higher motion capture quality.

At the same time, the software also supports editing and modification of recognized human body key points, smoothness, footstep details, etc. It can satisfy everything from the interest experience of ordinary players to the professional needs of hardcore players.
This is AIxPose, which has been developed by NetEase Interactive Entertainment AI Lab for many years, iteratively optimized and low-key based on professional art feedback. Video motion capture software. It is reported that the software has processed more than dozens of hours of video resources and has been used in the production process of game plot animations, popular dance animations and other resources. It has been verified by actual projects that a 1-minute dance animation may take more than 20 days to be produced by hand, but it only takes 3 days to produce with AIxPose assistance, and the entire process is shortened by more than 80%.
Recently, NetEase Interactive Entertainment AI Lab compiled the paper "Learning Analytical Posterior Probability" based on its experience in developing this software and related research work in the field of motion capture. for Human Mesh Recovery" was accepted by CVPR 2023, the top computer vision conference.

- Home page address: https://netease-gameai.github.io/ProPose/
- Paper address: https://netease-gameai.github.io/ProPose/static/assets/CVPR2023_ProPose.pdf
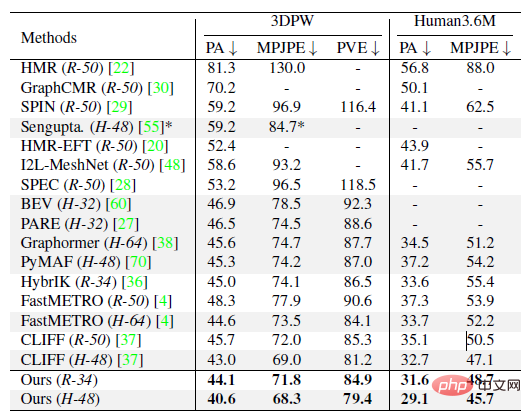
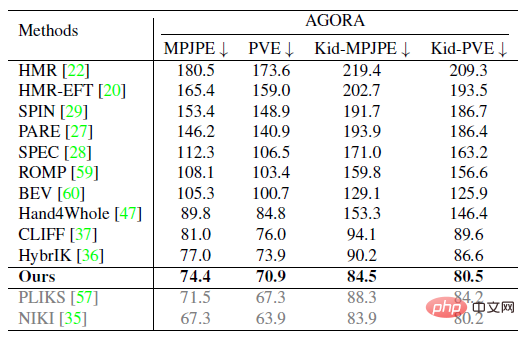
This paper innovatively proposes ProPose, a video motion capture technology based on posterior probability, which can achieve accurate three-dimensional human pose estimation under different settings such as single image and multi-sensor fusion. Technical accuracy is 19% higher than baseline probabilistic methods using priors, and outperforms past methods on the public datasets 3DPW, Human3.6M, and AGORA. In addition, for multi-sensor fusion tasks, this technology can also achieve higher accuracy than the baseline model without modifying the backbone of the neural network due to the introduction of new sensors.
Technical Background
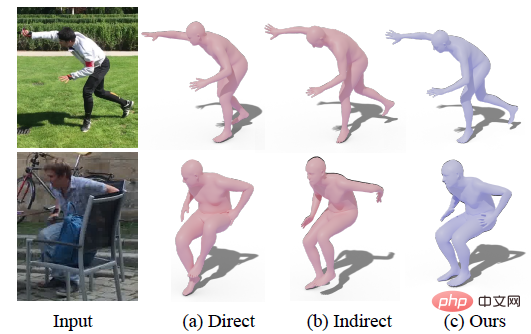
The task of this research is to predict human mesh recovery (hmr) from RGB images. The existing methods can be summarized into two Category: direct method and indirect method. The direct method uses a neural network to regress the rotational representation of human joints end-to-end (such as axis angle, rotation matrix, 6D vector, etc.), while the indirect method first predicts some intermediate representations (such as three-dimensional key points, segmentation, etc.), and then passes these intermediate Indicates that the joint rotation is obtained.
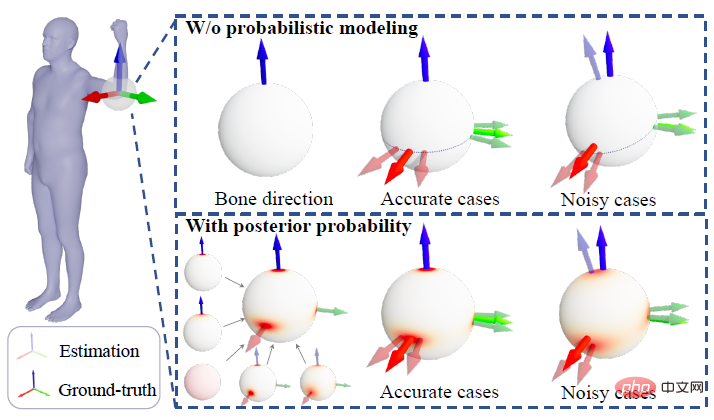
However, both types of methods have some problems. For direct methods, since this type of method requires the network to directly learn abstract representations such as rotation, compared with learning key points and segmentation, learning rotation is relatively difficult, so the results output by the network are sometimes difficult to align with the image and cannot be completed. Some large movements, such as the right foot in the first row in the picture below (a) cannot be fully extended back. In contrast, indirect methods generally produce higher accuracy, but the performance of such methods relies heavily on the accuracy of the intermediate representation. When the intermediate representation produces errors due to noise, it is easy for the final rotation to appear quite obvious. error, as shown in the left hand side of the second line in (b) below.
In addition to the aforementioned deterministic methods, there are also some methods to model the uncertainty of human posture by learning certain probability distributions, thereby Take noise into account to improve system robustness. Currently, the main probability modeling methods include multivariate Gaussian distribution, normalized flow, neural network implicit modeling, etc., but these probability distributions on non-SO (3) cannot truly reflect the uncertainty of joint rotation. For example, when the uncertainty is large, the local linearity assumption of the Gaussian distribution on SO (3) does not hold. A recent work directly uses the network to learn the parameters of the matrix Fisher distribution. Although this is a distribution on SO (3), the learning method of this method is similar to the direct method, and the convergence performance cannot be compared with the existing indirect method. .
In order to take into account both high accuracy and robustness and improve the performance of probabilistic methods, ProPose derives the analytical posterior probability of joint rotation, which can not only benefit from the changes brought by different observation variables With high accuracy, it can also measure uncertainty and reduce the impact of noise on the algorithm as much as possible. As shown in the figure below, for the input image, ProPose can measure the uncertainty of the joint rotation in various directions to a certain extent through the output probability distribution, such as the rotation of the right hand along the arm axis, the direction of the left arm swinging up and down, and the left calf. The degree of distance, etc.
Technical implementation
Human body modeling
##This study conducts probability construction of human posture module, the goal is to find the posterior probability p (R|d,⋯) of joint rotation R under some observed variables (such as bone orientation d, etc.).
Specifically, since the joint rotation of the human body is located on SO (3), and the unit bone orientation of the child joint relative to the parent joint is located on S^2, it can be based on these two Analyze the probability distribution on a manifold.
First of all, the matrix Fisher distribution MF (⋅) on SO (3) can be used as the prior distribution of the joint rotation R, as shown in the following formula, F∈R^(3×3 ) are the parameters of the distribution, c (F) is a normalizing constant, and tr represents the trace of the matrix.
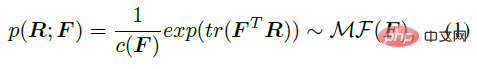
As shown in the following formula, F can be directly solved for the mean M and an aggregation term that represents the degree of distribution aggregation through SVD decomposition K. Among them, Δ=diag (1,1,|UV|) is a diagonal orthogonal matrix, which is used to ensure that the determinant of M is 1, so that it can fall in the special orthogonal group.
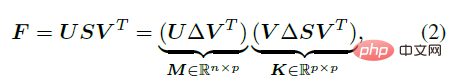
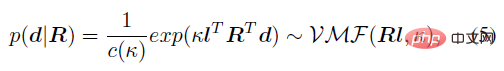
Using Bayesian theory, given the prior distribution p (R) and the likelihood function p (d|R), the posterior distribution of the joint rotation conditional on the bone orientation can be calculated. The analytical form of the posterior probability p (R|d):
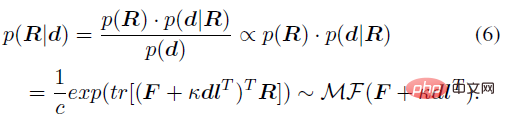
The above posterior probability only considers the orientation of the human skeleton as an observation quantity. Similarly, it can also be extended to other direction observation quantities d_i or rotation observation quantities D_j (which can be generated by other sensors) , such as IMUs, etc.), the analytical posterior probability is obtained in the following general form:
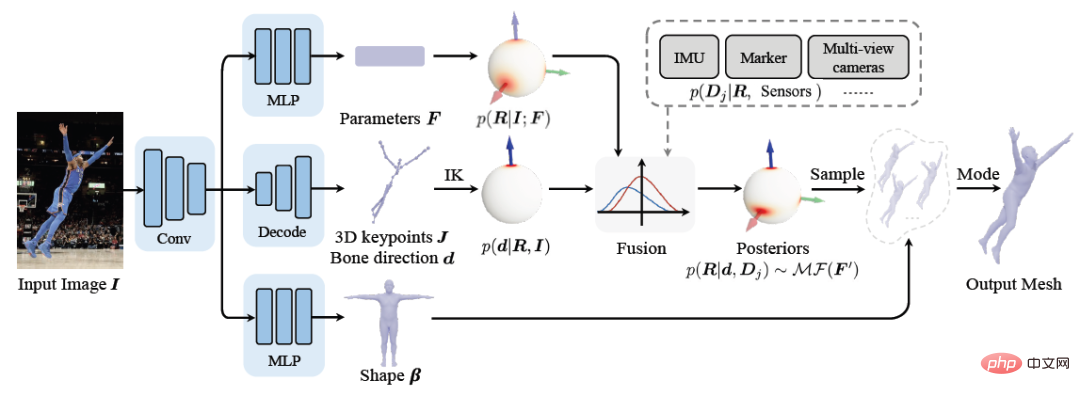
where κ_i and K_j are aggregation terms. g (⋅) is a mapping in the form of IK, which can convert direction observations into rotation estimates. It can adopt the simplest form such as g (d_i)=dl^T. Z_1 and Z_3 represent the set of direction observations and rotation observations respectively. Characteristics This section further explains that the posterior probability distribution has a higher probability than the prior probability distribution. degree of aggregation. The foregoing section introduces the analytical form of the posterior probability of human joint rotation, which is characterized by a new parameter F'. The posterior parameter F^' can be understood from another perspective, that is, F^' is the product of the mean term M that is the same as F and a new aggregation term K^': Where M^T dl^T=ll^T is a rank 1 real symmetric matrix, and K is also a real symmetric matrix, that is, the posterior aggregation term K' is also a real symmetric matrix. According to the staggered theorem about real symmetric matrices in matrix analysis, it can be obtained that the eigenvalues λ_i' of K' and the eigenvalues λ_i of K have the following inequality relationship: Considering that the eigenvalue of the aggregation term is equivalent to the singular value of the distribution parameter, and the singular value of the distribution parameter can reflect the confidence of the distribution, it can be concluded that when the likelihood term is non-zero, the posterior estimation ratio The prior estimate is more concentrated and can quickly converge to the mode preferred by the likelihood function, making it easier to learn. In addition to the prior probability method, another major benchmark method is to use inverse kinematics (IK) to directly calculate the rotation through the bone orientation. The following picture can intuitively show the posterior Comparison between probabilistic and deterministic IK methods. The above picture takes the human elbow joint as an example. The real three-dimensional coordinate axis represents the true value, and the transparent three-dimensional coordinate axis represents the estimated value. The first line represents the deterministic IK method. The modeling method behind this type of method is a vector representing the bone orientation. When the bone orientation is accurately estimated, the remaining one degree of freedom (twist) can be reduced to a circle (in the figure The dotted circle on the ball); when the bone orientation is estimated inaccurately, it will cause all possible estimates to deviate from the true value. The second line represents the posterior probability model of this study, which is a fusion of multiple different types of models. The red area on the sphere represents the probability of a certain rotation. Even if there is an error in the estimation of the bone orientation, this method may return it to the true state. value, because the noise of bone orientation can be mitigated as much as possible by a priori or other observations. Network framework diagram and loss function Based on the aforementioned theory and derivation, the following figure can be directly constructed frame diagram. A multi-branch network is used to estimate the prior distribution parameter F, the three-dimensional key point J (from which the bone orientation d is calculated), and the shape parameter β from a single image. The posterior probability is calculated through Bayes' rule, and finally the posture estimate can be obtained from the posterior distribution to output the human mesh. The selection of the loss function is relatively straightforward and is the weighted sum of the following four constraints, where L_J represents the key point constraint and L_β represents the shape parameter constraint. L_θ represents the attitude parameter constraint in matrix form, and L_s represents the attitude constraint after sampling the distribution. Regarding the constraints on the distribution, MAP is not used directly here because the numerical stability of the normalization parameters is considered. Regarding the sampling strategy, similar to the previous work, the matrix Fisher distribution is converted into the equivalent Bingham distribution in the quaternion form, and then obtained through rejection sampling, where the recommended distribution for rejection sampling adopts the angular central Gaussian distribution. In the experimental part, this study conducted a quantitative comparison with past methods on the public data sets Human3.6M, 3DPW, AGORA, and TotalCapture. It can be seen that the method of this study surpasses many previous methods. The last two gray rows in the table on the lower right are the work of the same period, and are listed here for the completeness of the list. 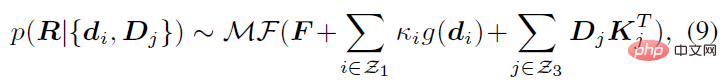
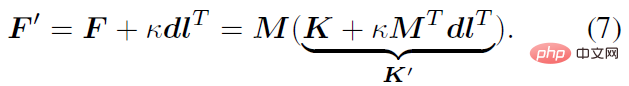
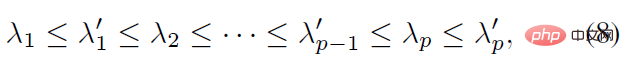
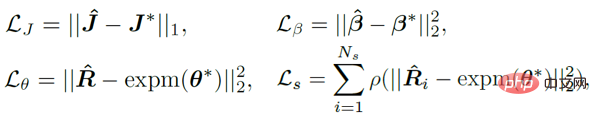
Experimental results
#The following figure shows the existing SOTA Qualitative comparison of methods HybrIK, PARE, and CLIFF shows that ProPose can achieve better results in some occlusion situations.

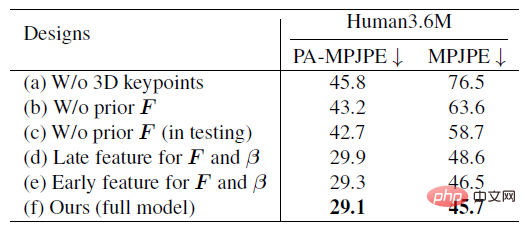
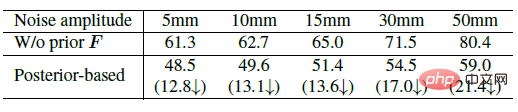
The following table shows a series of ablation experiments, mainly demonstrating the accuracy and robustness of ProPose. The benchmark methods include not using three-dimensional key points, not using priors, not using priors during testing, selecting features at different locations in the backbone network, etc. The table on the left below fully verifies that the proposed posterior probability distribution has higher accuracy. The table on the right below shows the comparison of the robustness to noise between the posterior method and the deterministic IK method. It can be seen that the posterior method can resist the interference of noise to a greater extent.
In addition to the above hmr tasks, this research also focuses on multi-sensor fusion tasks The evaluation was carried out on the above, and the effect of a single view and IMUs fusion is given below.
The above is the detailed content of Animation production efficiency increased by 80%! This AI software realizes high-precision video motion capture with one click. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 What are the types of return values of c language function? Summary of types of return values of c language function?
Apr 03, 2025 pm 11:18 PM
What are the types of return values of c language function? Summary of types of return values of c language function?
Apr 03, 2025 pm 11:18 PM
The return value types of C language function include int, float, double, char, void and pointer types. int is used to return integers, float and double are used to return floats, and char returns characters. void means that the function does not return any value. The pointer type returns the memory address, be careful to avoid memory leakage.结构体或联合体可返回多个相关数据。
 CS-Week 3
Apr 04, 2025 am 06:06 AM
CS-Week 3
Apr 04, 2025 am 06:06 AM
Algorithms are the set of instructions to solve problems, and their execution speed and memory usage vary. In programming, many algorithms are based on data search and sorting. This article will introduce several data retrieval and sorting algorithms. Linear search assumes that there is an array [20,500,10,5,100,1,50] and needs to find the number 50. The linear search algorithm checks each element in the array one by one until the target value is found or the complete array is traversed. The algorithm flowchart is as follows: The pseudo-code for linear search is as follows: Check each element: If the target value is found: Return true Return false C language implementation: #include#includeintmain(void){i
 How to use C language function pointer to find the maximum value of a one-dimensional array
Apr 03, 2025 pm 11:45 PM
How to use C language function pointer to find the maximum value of a one-dimensional array
Apr 03, 2025 pm 11:45 PM
Flexible application of function pointers: use comparison functions to find the maximum value of an array. First, define the comparison function type CompareFunc, and then write the comparison function compareMax(a, b). The findMax function accepts array, array size, and comparison function parameters, and uses the comparison function to loop to compare array elements to find the maximum value. This method has strong code reusability, reflects the idea of higher-order programming, and is conducive to solving more complex problems.
 What are c language function pointers and pointer functions? What's the difference?
Apr 03, 2025 pm 11:54 PM
What are c language function pointers and pointer functions? What's the difference?
Apr 03, 2025 pm 11:54 PM
A function pointer is a pointer to a function, and a pointer function is a function that returns a pointer. Function pointers point to functions, used to select and execute different functions; pointer functions return pointers to variables, arrays or other functions; when using function pointers, pay attention to parameter matching and checking pointer null values; when using pointer functions, pay attention to memory management and free dynamically allocated memory; understand the differences and characteristics of the two to avoid confusion and errors.
 What are the formats of function definition in C language?
Apr 03, 2025 pm 11:51 PM
What are the formats of function definition in C language?
Apr 03, 2025 pm 11:51 PM
The key elements of C function definition include: return type (defining the value returned by the function), function name (following the naming specification and determining the scope), parameter list (defining the parameter type, quantity and order accepted by the function) and function body (implementing the logic of the function). It is crucial to clarify the meaning and subtle relationship of these elements, and can help developers avoid "pits" and write more efficient and elegant code.
 What are the pointer parameters in the parentheses of the C language function?
Apr 03, 2025 pm 11:48 PM
What are the pointer parameters in the parentheses of the C language function?
Apr 03, 2025 pm 11:48 PM
The pointer parameters of C language function directly operate the memory area passed by the caller, including pointers to integers, strings, or structures. When using pointer parameters, you need to be careful to modify the memory pointed to by the pointer to avoid errors or memory problems. For double pointers to strings, modifying the pointer itself will lead to pointing to new strings, and memory management needs to be paid attention to. When handling pointer parameters to structures or arrays, you need to carefully check the pointer type and boundaries to avoid out-of-bounds access.
 Integers in C: a little history
Apr 04, 2025 am 06:09 AM
Integers in C: a little history
Apr 04, 2025 am 06:09 AM
Integers are the most basic data type in programming and can be regarded as the cornerstone of programming. The job of a programmer is to give these numbers meanings. No matter how complex the software is, it ultimately comes down to integer operations, because the processor only understands integers. To represent negative numbers, we introduced two's complement; to represent decimal numbers, we created scientific notation, so there are floating-point numbers. But in the final analysis, everything is still inseparable from 0 and 1. A brief history of integers In C, int is almost the default type. Although the compiler may issue a warning, in many cases you can still write code like this: main(void){return0;} From a technical point of view, this is equivalent to the following code: intmain(void){return0;}
 What do nested calls and recursive calls of c language functions mean respectively?
Apr 03, 2025 pm 11:09 PM
What do nested calls and recursive calls of c language functions mean respectively?
Apr 03, 2025 pm 11:09 PM
C language function calls can be divided into nested calls and recursive calls. Nested calls refer to calling other functions within a function, nesting them layer by layer. Recursive calls refer to the function itself calling itself, which can be used to deal with self-similar structure problems. The key difference is that the functions in nested calls are called in sequence, with independent interaction scopes, while the functions in recursive calls are constantly called, so you need to pay attention to the recursive basis and stack overflow issues. Which calling method to choose depends on the specific requirements and performance requirements of the problem.





