Understanding hierarchical clustering in one article (Python code)

First of all, clustering belongs to unsupervised learning of machine learning, and there are many methods, such as the well-known K-means. Hierarchical clustering is also a type of clustering and is also very commonly used. Next, I will briefly review the basic principles of K-means, and then slowly introduce the definition and hierarchical steps of hierarchical clustering, which will be more helpful for everyone to understand.

What is the difference between hierarchical clustering and K-means?

The working principle of K-means can be briefly summarized as:

• Determine the number of clusters (k)
• Randomly select k points from the data as centroids
• Assign all points to the nearest cluster centroid
• Calculate the centroid of the newly formed cluster
• Repeat steps 3 and 4

This is an iteration process until the centroids of newly formed clusters remain unchanged or the maximum number of iterations is reached.

But K-means has some shortcomings. We must decide the number of clusters K before the algorithm starts. But actually we don’t know how many clusters there should be, so we usually base it on our own understanding. Set a value first, which may lead to some deviations between our understanding and the actual situation.

Hierarchical clustering is completely different. It does not require us to specify the number of clusters at the beginning. Instead, it first completely forms the entire hierarchical clustering, and then by determining the appropriate distance, the corresponding cluster number and sum can be automatically found. clustering.

What is hierarchical clustering?

Let’s introduce what hierarchical clustering is from shallow to deep. Let’s start with a simple example.

Suppose we have the following points and we want to group them:

We can assign each of these points to a separate cluster, Just 4 clusters (4 colors):

Then based on the similarity (distance) of these clusters, the most similar (closest) points are grouped together and Repeat this process until only one cluster remains:

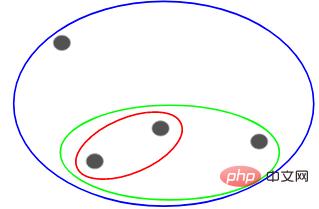
The above is essentially building a hierarchy. Let’s understand this first, and we will introduce its layering steps in detail later.

Types of hierarchical clustering

There are two main types of hierarchical clustering:

• Agglomerative hierarchical clustering
• Split hierarchical clustering

Agglomerative hierarchical clustering

First let all points become a separate cluster, and then continue to combine them through similarity until there is only one cluster in the end. This is agglomerative hierarchical clustering. The process is consistent with what we just said above.

Split hierarchical clustering

Split hierarchical clustering is just the opposite. It starts from a single cluster and gradually splits it until it cannot be split, that is, each point is a cluster.

So it doesn’t matter whether there are 10, 100, or 1000 data points, these points all belong to the same cluster at the beginning:

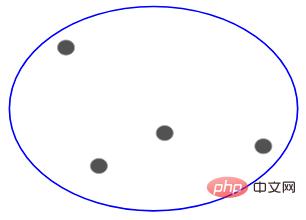
Now, Split the two furthest points in the cluster at each iteration, and repeat this process until each cluster contains only one point:

#The above process is splitting Hierarchical clustering.

Steps to perform hierarchical clustering

The general process of hierarchical clustering has been described above, but now comes the key point, how to determine the similarity between points?

This is one of the most important issues in clustering. The general method of calculating similarity is to calculate the distance between the centroids of these clusters. The points with minimum distance are called similar points and we can merge them or we can call it distance based algorithm.

Also in hierarchical clustering, there is a concept called proximity matrix, which stores the distance between each point. Below we use an example to understand how to calculate similarity, proximity matrix, and the specific steps of hierarchical clustering.

Case Introduction

Suppose a teacher wants to divide students into different groups. Now I have the scores of each student on the assignment, and I want to divide them into groups based on these scores. There is no set goal here as to how many groups to have. Since the teacher does not know which type of students should be assigned to which group, it cannot be solved as a supervised learning problem. Below, we will try to apply hierarchical clustering to classify students into different groups.

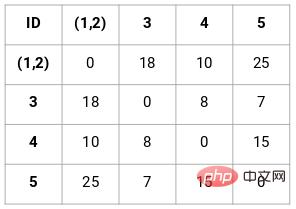
The following are the results of 5 students:

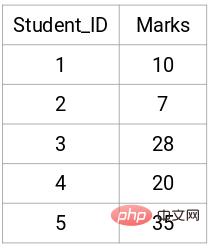
Create a proximity matrix

First, we need to create a proximity matrix, which stores the distance between each point, so we can get a shape of n Square matrix of X n.

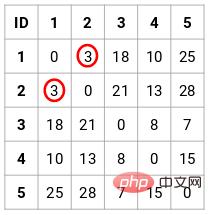
In this case, the following 5 x 5 proximity matrix can be obtained:

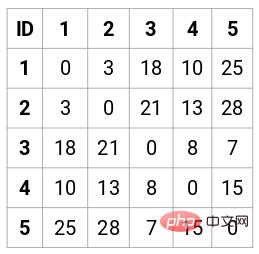
There are two points to note in the matrix:

• The diagonal elements of a matrix are always 0 because the distance of a point from itself is always 0
• Use the Euclidean distance formula to calculate the distance of non-diagonal elements

For example, if we want to calculate the distance between points 1 and 2, the calculation formula is:

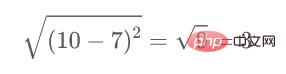
Similarly, fill in the remaining elements of the proximity matrix after completing this calculation method.

Perform hierarchical clustering

This is implemented using agglomerative hierarchical clustering.

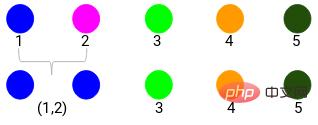
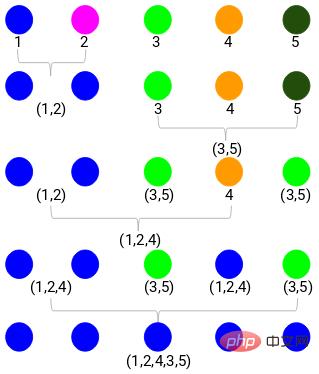
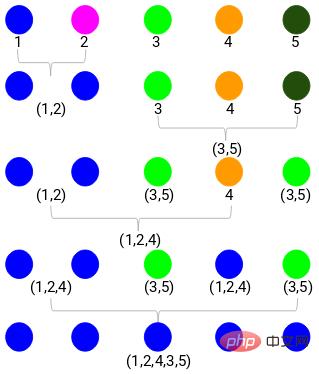
Step 1: First, we assign all points into a single cluster:

Here different colors represent different clusters, 5 of them in our data point, that is, there are 5 different clusters.

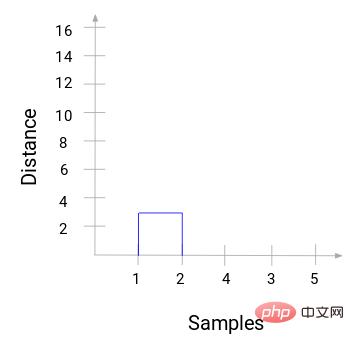
Step 2: Next, we need to find the minimum distance in the proximity matrix and merge the points with the smallest distance. Then we update the proximity matrix:

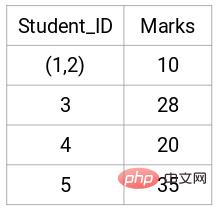
The minimum distance is 3, so we will merge points 1 and 2:

## Let’s look at the updated clusters and update the proximity matrix accordingly:

# After the update, we take the largest value (7, 10) between the two points 1 and 2 to replace the value of this cluster. Of course, in addition to the maximum value, we can also take the minimum or average value. We will then calculate the proximity matrix for these clusters again:

Step 3: Repeat step 2 until only one cluster remains.

After repeating all the steps, we will get the merged clusters as shown below:

This is how agglomerative hierarchical clustering works. But the problem is we still don’t know how many groups to divide into? Is it group 2, 3, or 4?

Let’s start with how to choose the number of clusters.

How to choose the number of clusters?

In order to obtain the number of clusters for hierarchical clustering, we use a concept called a dendrogram.

Through the dendrogram, we can more easily select the number of clusters.

Back to the above example. When we merge two clusters, the dendrogram accordingly records the distance between these clusters and represents it graphically. The following is the original state of the dendrogram. The horizontal axis records the mark of each point, and the vertical axis records the distance between points:

When merging two When there are clusters, they will be connected in the dendrogram, and the height of the connection is the distance between the points. The following is the process of hierarchical clustering we just performed.

Then start drawing a tree diagram of the above process. Starting from merging samples 1 and 2, the distance between these two samples is 3.

You can see that 1 and 2 have been merged. The vertical line represents the distance between 1 and 2. In the same way, all the steps of merging clusters are drawn according to the hierarchical clustering process, and finally a dendrogram like this is obtained:

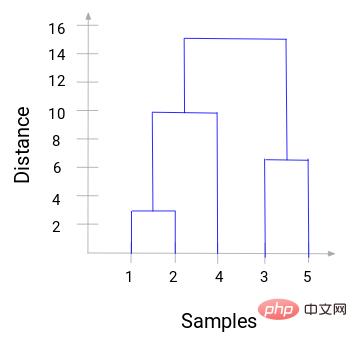
With a dendrogram, we can clearly visualize the steps of hierarchical clustering. The farther apart the vertical lines in the dendrogram are, the greater the distance between clusters.

With this dendrogram, it is much easier for us to determine the number of clusters.

Now we can set a threshold distance and draw a horizontal line. For example, we set the threshold to 12 and draw a horizontal line as follows:

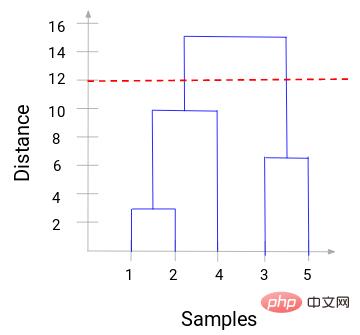
As you can see from the intersection point, the number of clusters is the intersection of the threshold horizontal line and the vertical line quantity (red line intersects 2 vertical lines, we will have 2 clusters). Corresponding to the abscissa, one cluster will have a sample set (1,2,4), and the other cluster will have a sample set (3,5).

In this way, we solve the problem of determining the number of clusters in hierarchical clustering through a dendrogram.

Python code practical case

The above is the theoretical basis, and anyone with a little mathematical foundation can understand it. Here's how to implement this process using Python code. Here is a customer segmentation data to show.

The data set and code are in my GitHub repository:

​​https://github.com/xiaoyusmd/PythonDataScience​​

If you find it helpful, please give it a star!

This data comes from the UCI machine learning library. Our aim is to segment wholesale distributors’ customers based on their annual spend on different product categories such as milk, groceries, regions, etc.

First standardize the data to make all data in the same dimension easy to calculate, and then apply hierarchical clustering to segment customers.

from sklearn.preprocessing import normalize
data_scaled = normalize(data)
data_scaled = pd.DataFrame(data_scaled, columns=data.columns)
import scipy.cluster.hierarchy as shc
plt.figure(figsize=(10, 7))
plt.title("Dendrograms")
dend = shc.dendrogram(shc.linkage(data_scaled, method='ward'))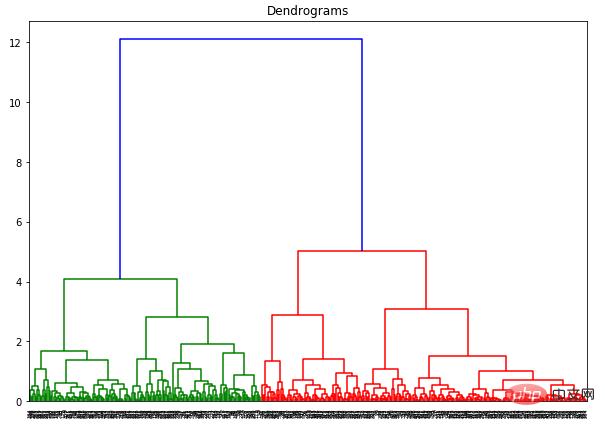

The x-axis contains all samples, and the y-axis represents the distance between these samples. The vertical line with the largest distance is the blue line. Suppose we decide to cut the dendrogram with a threshold of 6:

plt.figure(figsize=(10, 7))
plt.title("Dendrograms")
dend = shc.dendrogram(shc.linkage(data_scaled, method='ward'))
plt.axhline(y=6, color='r', linestyle='--')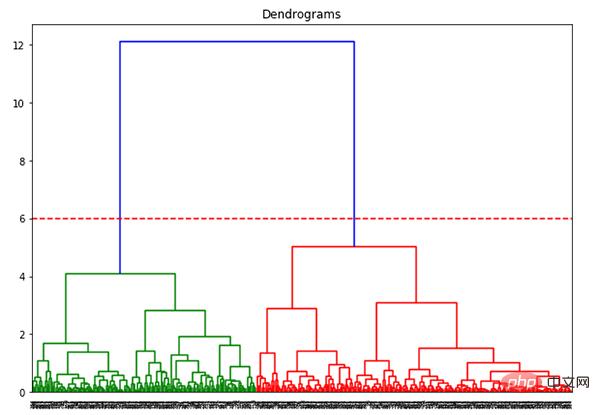

Now that we have two clusters, we need to Apply hierarchical clustering on clusters:

from sklearn.cluster import AgglomerativeClustering
cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='ward')
cluster.fit_predict(data_scaled)

Since we have defined 2 clusters, we can see the values ​​of 0 and 1 in the output. 0 represents a point belonging to the first cluster, and 1 represents a point belonging to the second cluster.

plt.figure(figsize=(10, 7))
plt.scatter(data_scaled['Milk'], data_scaled['Grocery'], c=cluster.labels_)

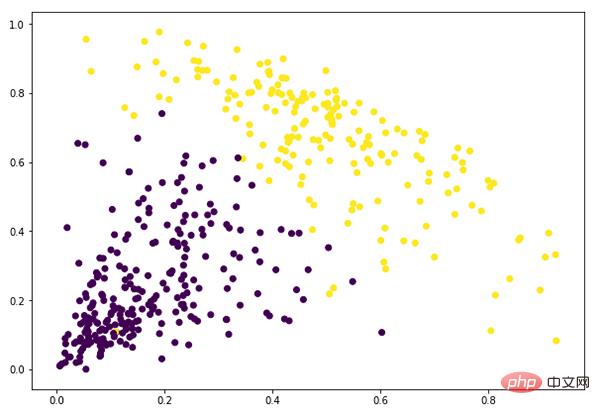
At this point we have successfully completed clustering.

The above is the detailed content of Understanding hierarchical clustering in one article (Python code). For more information, please follow other related articles on the PHP Chinese website!