Training ViT and MAE reduces the amount of calculation by half! Sea and Peking University jointly proposed the efficient optimizer Adan, which can be used for deep models

Since Google proposed Vision Transformer (ViT), ViT has gradually become the default backbone for many visual tasks. With the ViT structure, SoTA has been further improved for many visual tasks, including image classification, segmentation, detection, recognition, etc.

However, training ViT is not easy. In addition to requiring more complex training techniques, the amount of calculation required for model training is often much greater than that of previous CNNs. Recently, the research teams of Singapore Sea AI LAB (SAIL) and Peking University ZERO Lab jointly proposed a new deep model optimizer Adan, which can complete ViT with only half the calculation amount train.

##Paper link: https://arxiv.org/pdf/2208.06677.pdf

Code link: ​https://github.com/sail-sg/Adan​

In addition, under the same calculation amount , Adan has worked in multiple scenarios (involving CV, NLP, RL), multiple training methods (supervised and self-supervised) and multiple network structures/algorithms (Swin, ViT, ResNet, ConvNext, MAE, LSTM, BERT, Transformer-XL, PPO algorithm), all obtained performance improvements.

The code, configuration files, and training logs are all open source.

Training paradigm and optimizer of deep models

With the introduction of ViT, the training methods of deep models have become more and more complex. Common training techniques include complex data enhancement (such as MixUp, CutMix, AutoRand), label processing (such as label smoothing and noise label), moving average of model parameters, random network depth, dropout, etc. With the mixed application of these techniques, the generalization and robustness of the model have been improved, but along with it, the computational complexity of model training has become larger and larger.

On ImageNet 1k, the number of training epochs has increased from 90 just proposed by ResNet to 300 commonly used for training ViT. Even for some self-supervised learning models, such as MAE and ViT, the number of pre-training epochs has reached 1.6k. The increase in training epoch means that the training time is greatly extended, which sharply increases the cost of academic research or industrial implementation. A common solution at present is to increase the training batch size and assist in parallel training to reduce training time. However, the accompanying problem is that a large batch size often means a decrease in performance, and the larger the batch size, the more obvious the situation.

This is mainly because the number of model parameter updates decreases sharply as the batch size increases. The current optimizer cannot achieve rapid training of the model with a small number of updates under complex training paradigms, which further aggravates the increase in the number of model training epochs.

So, is there a new optimizer that can train deep models faster and better with fewer parameter updates? While reducing the number of training epochs, can it also alleviate the negative impact of increasing batch size?

Ignored impulse

To speed up the convergence speed of the optimizer, the most direct way is to introduce impulse. The deep model optimizers proposed in recent years all follow the impulse paradigm used in Adam - Heavy Sphere Method:

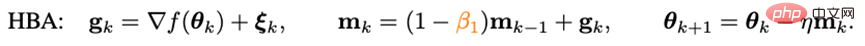
where g_k is random noise, m_k is moment, and eta is learning rate. Adam changed the update of m_k from the cumulative form to the moving average form, and introduced the second-order moment (n_k) to scale the learning rate, that is:

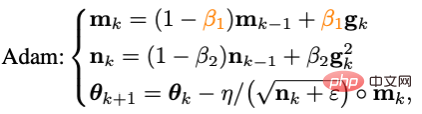
However, as Adam failed to train the original ViT, its improved version AdamW gradually became the first choice for training ViT and even ConvNext. However, AdamW does not change the impulse paradigm in Adam, so when the batch size exceeds 4,096, the performance of ViT trained by AdamW will drop sharply.

In the field of traditional convex optimization, there is an impulse technique that is as famous as the heavy ball method - Nesterov impulse algorithm:

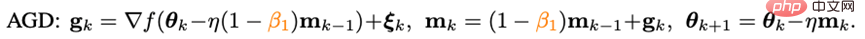
Nesterov impulse algorithm has a faster theoretical convergence speed than the gravity ball method on smooth and generally convex problems, and can theoretically withstand larger batches size. Different from the weighted ball method, the Nesterov algorithm does not calculate the gradient at the current point, but uses the impulse to find an extrapolation point, and then accumulates the impulse after calculating the gradient at this point.

Extrapolation points can help the Nesterov algorithm to perceive the geometric information around the current point in advance. This characteristic makes Nesterov impulse more suitable for complex training paradigms and model structures (such as ViT), because it does not simply rely on past impulses to bypass sharp local minimum points, but adjusts them by observing the surrounding gradients in advance. Updated directions.

Although the Nesterov impulse algorithm has certain advantages, it has rarely been applied and explored in deep optimizers. One of the main reasons is that the Nesterov algorithm needs to calculate the gradient at the extrapolation point and update it at the current point. During this period, it requires multiple model parameter reloads and artificial back-propagation (BP) at the extrapolation point. These inconveniences greatly limit the application of Nesterov impulse algorithm in deep model optimizers.

Adan Optimizer

By combining the rewritten Nesterov impulse with the adaptive optimization algorithm, and introducing decoupled weight attenuation, the final Adan optimizer can be obtained. Using extrapolation points, Adan can perceive the surrounding gradient information in advance, thereby efficiently escaping from sharp local minimum areas to increase the generalization of the model.

1) Adaptive Nesterov impulse

In order to solve the problem of multiple model parameter overloading in the Nesterov impulse algorithm Problem, the researchers first rewritten Nesterov:

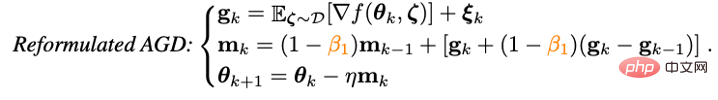
It can be proved that the rewritten Nesterov impulse algorithm is equivalent to the original algorithm, and the iteration points of the two can be converted into each other, and the final convergence point is the same. It can be seen that by introducing the differential term of the gradient, manual parameter overloading and artificial BP at the extrapolation point can be avoided.

Combine the rewritten Nesterov impulse algorithm with the adaptive class optimizer - replace the update of m_k from the cumulative form to the moving average form, and use the second-order moment to adjust the learning rate Zoom:

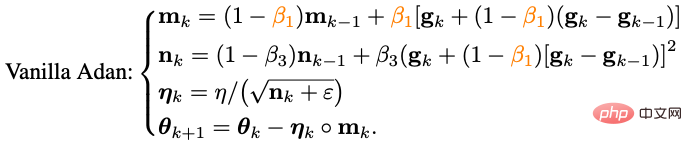
So far we have obtained the basic version of Adan’s algorithm.

2) Impulse of gradient difference

It can be found that the update of m_k couples the gradient and the gradient difference in Together, but in actual scenarios, two items with different physical meanings often need to be processed separately, so researchers introduce the impulse v_k of the gradient difference:

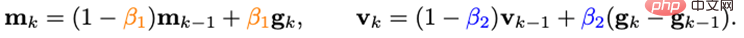
Here set different impulse/average coefficients for the impulse of the gradient and its difference. The gradient difference term can slow down the update of the optimizer when adjacent gradients are inconsistent, and conversely, speed up the update when the gradient directions are consistent.

3) Decoupled weight decay

For the objective function with L2 weight regularization, the currently popular AdamW optimizer has achieved better performance on ViT and ConvNext by decoupling L2 regularization and training loss. However, the decoupling method used by AdamW is biased toward heuristics, and currently there is no theoretical guarantee of its convergence.

Based on the idea of ​​decoupling L2 regularity, a decoupled weight attenuation strategy is also introduced to Adan. At present, each iteration of Adan can be seen as minimizing some first-order approximation of the optimization objective F:

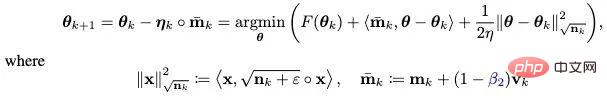
Due to the L2 weight in F The regularization is so simple and smooth that a first-order approximation to it is not necessary. Therefore, you can only perform a first-order approximation to the training loss and ignore the L2 weight regularization, then the last iteration of Adan will become:

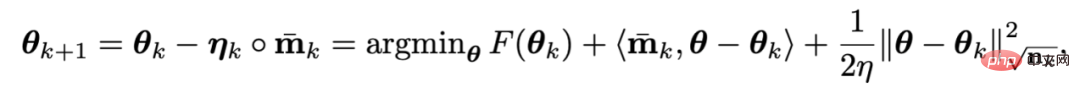
Interesting What is more, it can be found that the update criterion of AdamW is the first-order approximation of the Adan update criterion when the learning rate eta is close to 0. Therefore, a reasonable explanation can be given to Adan or even AdamW from the perspective of proximal operator instead of the original heuristic improvement.

4) Adan optimizer

combines the two improvements 2) and 3) into the basic version of Adan , the following Adan optimizer can be obtained.

Adan combines the advantages of the adaptive optimizer, Nesterov impulse and decoupled weight decay strategy, and can withstand larger learning rates and batches size, and can implement dynamic L2 regularization of model parameters.

5) Convergence analysis

##Here we skip the complicated mathematical analysis process and only give the conclusion:

Theorem: In both cases where the Hessian-smooth condition is given or not, the convergence speed of the Adan optimizer can reach the already achieved level in non-convex stochastic optimization problems. The theoretical lower bound is known, and this conclusion still holds with a decoupled weight decay strategy.

Experimental results

1. CV scenario

1) Supervised learning ——ViT model

For the ViT model, the researchers tested the performance of Adan on the ViT and Swin structures.

It can be seen that, for example, on ViT-small, ViT-base, Swin-tiny and Swin-base, Adan only consumes half of the The computing resources are close to the results obtained by the SoTA optimizer, and under the same calculation amount, Adan shows great advantages in both ViT models.

In addition, the performance of Adan was also tested under large batch size:

You can see , Adan performs well under various batch sizes, and also has certain advantages over the optimizer (LAMB) designed for large batch sizes.

2) Supervised learning - CNN model

In addition to the more difficult-to-train ViT model, researchers also tested Adan's performance on CNN models with relatively few sharp local minimum points - including the classic ResNet and the more advanced ConvNext. The results are as follows:

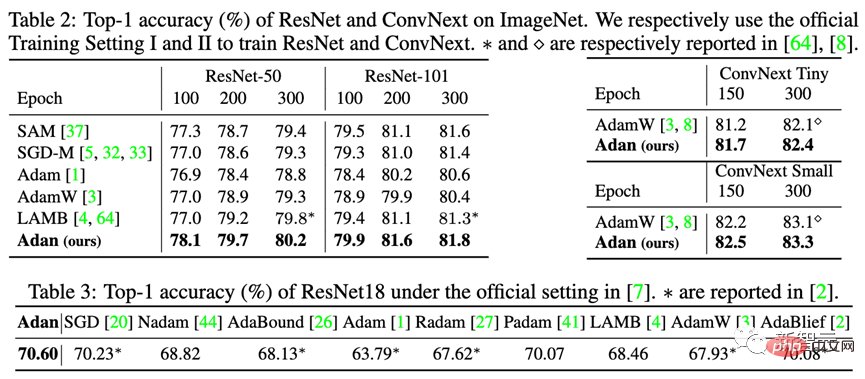
It can be observed that whether it is ResNet or ConvNext, Adan can achieve performance beyond SoTA within about 2/3 of the training epochs. .

3) Unsupervised learning

Under the unsupervised training framework, researchers The performance of Adan was tested on the latest proposed MAE. The results are as follows:

Consistent with the conclusion of supervised learning, Adan only consumes half the calculation amount to equal or even surpass the original SoTA. Optimizer, and when the training epoch is smaller, Adan’s advantage becomes more obvious.

2. NLP scenario

1) Supervised learning

On the supervised learning task of NLP, observe Adan's performance on the classic LSTM and the advanced Transformer-XL.

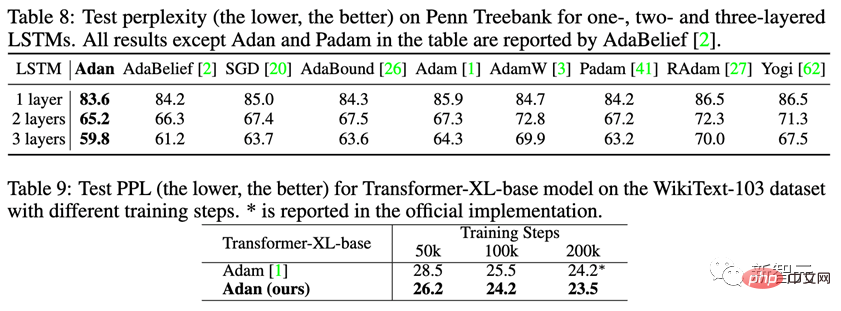
Adan shows consistent superiority on the above two networks. And for Transformer-XL, Adan tied the default Adam optimizer in half the number of training steps.

2) Unsupervised learning

In order to test Adan’s unsupervised learning in NLP scenarios Model training status on the task. The researchers trained BERT from scratch: after 1000k pre-training iterations, the performance of the Adan-trained model was tested on 7 subtasks of the GLUE dataset, and the results were as follows:

Adan showed great advantages in all 7 word and sentence classification tasks tested. It is worth mentioning that the results of the BERT-base model trained by Adan even exceeded the BERT-large trained by Adam on some subtasks (such as RTE, CoLA and SST-2).

3. RL Scenario

The researchers replaced the optimizer in the PPO algorithm commonly used in RL with Adan, and tested Adan on 4 games in the MuJoCo engine performance. In 4 games, the PPO algorithm using Adan as the network optimizer can always obtain higher rewards.

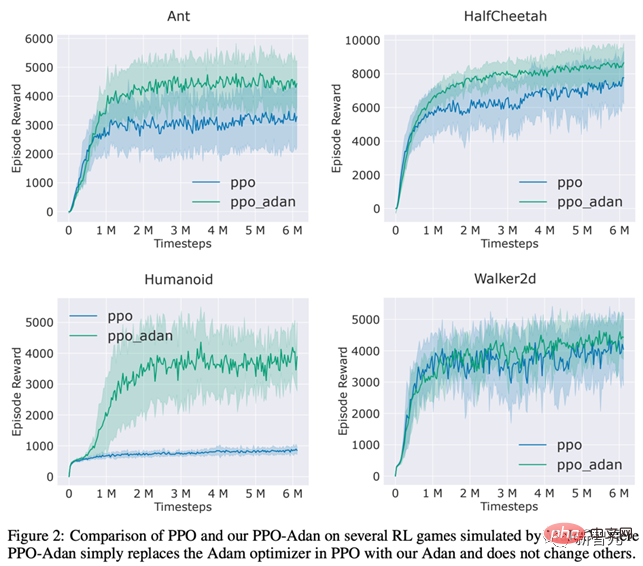
Adan also shows great potential in RL network training.

Conclusion and Outlook

The Adan optimizer introduces a new impulse paradigm to current deep model optimizers. Achieve fast training of models under complex training paradigms with fewer updates.

Experiments show that Adan can equal the existing SoTA optimizer with only 1/2-2/3 of the calculation amount.

Adan is used in multiple scenarios (involving CV, NLP, RL), multiple training methods (supervised and self-supervised) and multiple network structures (ViT, CNN, LSTM, Transformer etc.), all show great performance advantages. In addition, the convergence speed of the Adan optimizer has reached the theoretical lower bound in non-convex stochastic optimization.

The above is the detailed content of Training ViT and MAE reduces the amount of calculation by half! Sea and Peking University jointly proposed the efficient optimizer Adan, which can be used for deep models. For more information, please follow other related articles on the PHP Chinese website!